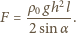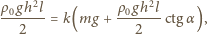Zadanie ZF-K44-487
o zadaniu...
- Publikacja w Delcie: marzec 2010
- Publikacja elektroniczna: 6 lipca 2010
Na końcach nieważkiego pręta o długości
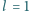 m znajdują się dwie
jednakowe masy punktowe
m znajdują się dwie
jednakowe masy punktowe
 Pręt jest podtrzymywany w środku,
wokół którego może się swobodnie obracać, i znajduje się w polu
grawitacyjnym Ziemi, które uznajemy za takie, jakby cała masa Ziemi była
skupiona w jej środku. Obliczyć okres małych drgań pręta wokół pionowego
położenia równowagi.
Pręt jest podtrzymywany w środku,
wokół którego może się swobodnie obracać, i znajduje się w polu
grawitacyjnym Ziemi, które uznajemy za takie, jakby cała masa Ziemi była
skupiona w jej środku. Obliczyć okres małych drgań pręta wokół pionowego
położenia równowagi.
Jaka będzie odpowiedź, jeśli pręt jest jednorodny, a pozostałe dane – niezmienione?
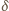 , a połowę długości pręta
oznaczmy dla wygody jako
, a połowę długości pręta
oznaczmy dla wygody jako
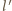 . W pierwszym rzędzie względem
. W pierwszym rzędzie względem
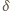 oraz względem stosunku
oraz względem stosunku
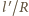 odległości końców pręta od środka
Ziemi wynoszą
odległości końców pręta od środka
Ziemi wynoszą
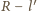 oraz
oraz
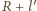 (gdzie
(gdzie
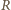 jest promieniem
Ziemi), a siły działające na końce są równe
jest promieniem
Ziemi), a siły działające na końce są równe
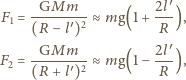
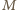 – masa Ziemi,
– masa Ziemi,
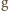 – przyspieszenie ziemskie. W tym
samym przybliżeniu nietrudno również wyznaczyć kąty między kierunkami
tych sił a osią pręta. Są one równe
– przyspieszenie ziemskie. W tym
samym przybliżeniu nietrudno również wyznaczyć kąty między kierunkami
tych sił a osią pręta. Są one równe
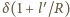 i
i
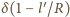 , a stąd
momenty sił
, a stąd
momenty sił
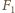 i
i
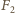 wynoszą
wynoszą
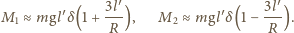
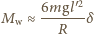
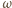 jest równy ilorazowi
współczynnika stojącego przed
jest równy ilorazowi
współczynnika stojącego przed
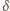 w powyższym wzorze przez moment
bezwładności
w powyższym wzorze przez moment
bezwładności
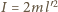 :
:
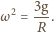
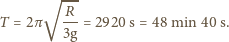
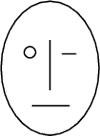
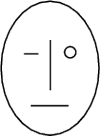
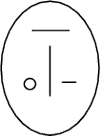
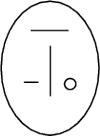
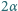 , którego dwusieczna jest pionowa.
Wzdłuż tych półprostych mogą ślizgać się bez tarcia końce jednorodnego
pręta o długości
, którego dwusieczna jest pionowa.
Wzdłuż tych półprostych mogą ślizgać się bez tarcia końce jednorodnego
pręta o długości
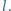 W którym przypadku poziome położenie pręta jest
położeniem równowagi trwałej – gdy wierzchołek kąta jest na górze, czy
gdy jest na dole? Dla przypadku równowagi trwałej podać wzór na
częstotliwość małych drgań pręta wokół tego położenia.
W którym przypadku poziome położenie pręta jest
położeniem równowagi trwałej – gdy wierzchołek kąta jest na górze, czy
gdy jest na dole? Dla przypadku równowagi trwałej podać wzór na
częstotliwość małych drgań pręta wokół tego położenia.
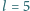 cm
i grubości
cm
i grubości
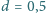 cm, drgającej z amplitudą
cm, drgającej z amplitudą
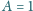 cm
i częstotliwością
cm
i częstotliwością
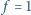 kHz wzdłuż osi prostopadłej do płytki.
kHz wzdłuż osi prostopadłej do płytki.
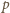 jest
równa
jest
równa
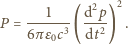
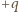 i
i
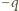 odległych o
odległych o
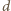 nazywamy iloczyn
nazywamy iloczyn
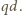
 . Jaka masa strzępków
balonika znajduje się na zewnątrz koła o promieniu
. Jaka masa strzępków
balonika znajduje się na zewnątrz koła o promieniu
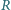 i środku
w punkcie, w którym znajdował się balonik? Masa balonika była
równa
i środku
w punkcie, w którym znajdował się balonik? Masa balonika była
równa
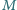 .
.
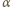 do poziomu spadną
w odległości
do poziomu spadną
w odległości
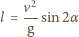
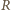 ,
jeśli
,
jeśli
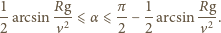
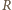 do masy całkowitej balonika jest równy stosunkowi powierzchni
do masy całkowitej balonika jest równy stosunkowi powierzchni
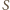 pasa
na powierzchni wybuchającego balonika, leżącego między kątami
pasa
na powierzchni wybuchającego balonika, leżącego między kątami
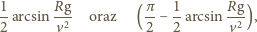
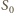 . Oznaczając przez
. Oznaczając przez
 promień balonika, otrzymujemy:
promień balonika, otrzymujemy:
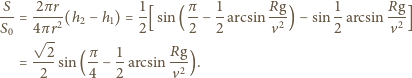
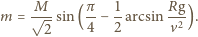

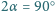 i pionowej osi symetrii. Znajdująca się w rynience piłeczka co
i pionowej osi symetrii. Znajdująca się w rynience piłeczka co
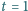 s odbija się od ścianki rynienki, na przemian w punktach
s odbija się od ścianki rynienki, na przemian w punktach
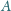 i
i
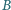 znajdujących się na tej samej wysokości. Znaleźć
najmniejszą i największą prędkość piłeczki w czasie tego ruchu.
znajdujących się na tej samej wysokości. Znaleźć
najmniejszą i największą prędkość piłeczki w czasie tego ruchu.
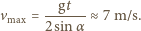
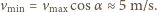
 , liczba zwojów na jednostkę jej długości –
, liczba zwojów na jednostkę jej długości –
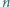 ,
długość pręta –
,
długość pręta –
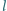 , ładunek każdej z kulek –
, ładunek każdej z kulek –
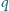 , masa
kulki –
, masa
kulki –
 , a masę samego pręta można pominąć. Jeśli nić
nie wywiera na pręt żadnego momentu siły, to jakim wzorem jest dana
prędkość kątowa, jaką uzyska pręt po włączeniu zasilania zwojnicy prądem
stałym o natężeniu
, a masę samego pręta można pominąć. Jeśli nić
nie wywiera na pręt żadnego momentu siły, to jakim wzorem jest dana
prędkość kątowa, jaką uzyska pręt po włączeniu zasilania zwojnicy prądem
stałym o natężeniu
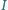 ?
?
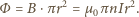
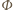 po czasie równa
jest krążeniu pola elektrycznego. Wybieramy kontur będący okręgiem
o średnicy
po czasie równa
jest krążeniu pola elektrycznego. Wybieramy kontur będący okręgiem
o średnicy
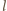 i wyznaczamy siłę
i wyznaczamy siłę
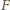 działającą na każdą
z kulek
działającą na każdą
z kulek
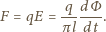
 uzyskana przez kulki jest równa całce z
uzyskana przez kulki jest równa całce z
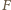 po czasie, podzielonej przez masę. Stąd znajdujemy szukaną prędkość
kątową
po czasie, podzielonej przez masę. Stąd znajdujemy szukaną prędkość
kątową
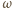 :
:
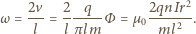
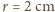 ,
,
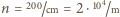 ,
,
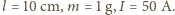 Aby ocenić wartość
Aby ocenić wartość
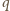 załóżmy, że kulkę o promieniu
załóżmy, że kulkę o promieniu
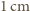 ładujemy napięciem
ładujemy napięciem
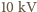 (z maszyny elektrostatycznej). Wynikiem jest
(z maszyny elektrostatycznej). Wynikiem jest
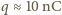 i ostatecznie
i ostatecznie
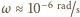 . Jak widać, efektu pobudzenia
ruchu pręta nie da się zaobserwować w tych warunkach.
. Jak widać, efektu pobudzenia
ruchu pręta nie da się zaobserwować w tych warunkach.
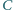 naładowany do
napięcia
naładowany do
napięcia
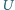 oraz 2 nienaładowane kondensatory, których pojemności
oraz 2 nienaładowane kondensatory, których pojemności
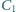 i
i
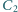 możemy wybrać według życzenia. Kondensatory można
dowolnie łączyć w obwód, rozłączać i łączyć ponownie. Dobrać wartości
możemy wybrać według życzenia. Kondensatory można
dowolnie łączyć w obwód, rozłączać i łączyć ponownie. Dobrać wartości
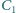 i
i
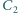 oraz zaprojektować takie połączenia i przełączenia, aby
korzystając tylko z energii zmagazynowanej w pierwszym kondensatorze
uzyskać baterię naładowaną do napięcia
oraz zaprojektować takie połączenia i przełączenia, aby
korzystając tylko z energii zmagazynowanej w pierwszym kondensatorze
uzyskać baterię naładowaną do napięcia
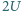 i o maksymalnej możliwej
pojemności zastępczej.
i o maksymalnej możliwej
pojemności zastępczej.
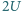 , jeśli poza
kondensatorem naładowanym dysponujemy tylko jednym kondensatorem
dodatkowym oraz zwojnicą? Jeśli tak, to jaką pojemność baterii można
uzyskać?
, jeśli poza
kondensatorem naładowanym dysponujemy tylko jednym kondensatorem
dodatkowym oraz zwojnicą? Jeśli tak, to jaką pojemność baterii można
uzyskać?

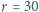 cm obraca się ze stałą prędkością kątową
w płaszczyźnie pionowej. W pewnym momencie od koła oderwało się małe
ciało (np. kropla wody), a po pewnym czasie spadło na to samo miejsce koła,
przyklejając się bez straty energii (tzn. prędkość ciała i brzegu koła w miejscu
upadku były jednakowe – zob. rys. 1). Podać co najmniej dwie wartości
prędkości kątowej
cm obraca się ze stałą prędkością kątową
w płaszczyźnie pionowej. W pewnym momencie od koła oderwało się małe
ciało (np. kropla wody), a po pewnym czasie spadło na to samo miejsce koła,
przyklejając się bez straty energii (tzn. prędkość ciała i brzegu koła w miejscu
upadku były jednakowe – zob. rys. 1). Podać co najmniej dwie wartości
prędkości kątowej
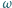 , przy których takie zdarzenie jest możliwe. Opór
powietrza pominąć.
, przy których takie zdarzenie jest możliwe. Opór
powietrza pominąć.
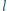 jechał ze stałą prędkością po torze początkowo
prostoliniowym, który począwszy od pewnego punktu przechodzi w łuk okręgu
o promieniu znacznie większym od
jechał ze stałą prędkością po torze początkowo
prostoliniowym, który począwszy od pewnego punktu przechodzi w łuk okręgu
o promieniu znacznie większym od
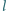 , bez przechyłu bocznego. Wózki
wagonu są rozmieszczone w odległości
, bez przechyłu bocznego. Wózki
wagonu są rozmieszczone w odległości
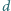 od jego środka, ich rozmiary
są małe, a masa wagonu jest rozłożona równomiernie wzdłuż jego długości.
Niech
od jego środka, ich rozmiary
są małe, a masa wagonu jest rozłożona równomiernie wzdłuż jego długości.
Niech
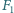 będzie wartością siły poziomej działającej na szynę ze strony
pierwszego wózka po jego wejściu w łuk, gdy drugi wózek jeszcze poruszał się
po prostej, natomiast
będzie wartością siły poziomej działającej na szynę ze strony
pierwszego wózka po jego wejściu w łuk, gdy drugi wózek jeszcze poruszał się
po prostej, natomiast
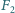 – wartością tej siły, gdy cały wagon znalazł się na
łuku. Jeśli
– wartością tej siły, gdy cały wagon znalazł się na
łuku. Jeśli
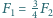 , to jaki wynika stąd wniosek na temat stosunku
, to jaki wynika stąd wniosek na temat stosunku
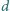 do
do
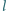 ?
?
 – prędkość wagonu,
– prędkość wagonu,
 – jego masa,
– jego masa,
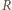 – promień
łuku. Ruch wagonu po wejściu pierwszego wózka w zakręt jest obrotem
wokół osi przechodzącej przez drugi wózek, z przyspieszeniem kątowym
równym
– promień
łuku. Ruch wagonu po wejściu pierwszego wózka w zakręt jest obrotem
wokół osi przechodzącej przez drugi wózek, z przyspieszeniem kątowym
równym
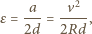
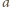 jest przyspieszeniem dośrodkowym pierwszego wózka.
To wyrażenie należy przyrównać do ilorazu momentu siły
jest przyspieszeniem dośrodkowym pierwszego wózka.
To wyrażenie należy przyrównać do ilorazu momentu siły
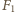 (której
ramieniem jest odcinek
(której
ramieniem jest odcinek
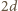 ) przez moment bezwładności
) przez moment bezwładności
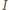 względem osi obrotu. Zgodnie z twierdzeniem Steinera
względem osi obrotu. Zgodnie z twierdzeniem Steinera
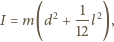
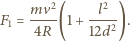
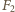 była równa połowie siły odśrodkowej
była równa połowie siły odśrodkowej
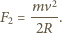
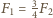 znajdujemy
znajdujemy
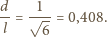
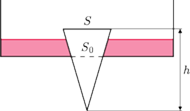
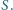 Dla jakiej największej gęstości korka
Dla jakiej największej gęstości korka
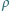 można, nalewająć do naczynia wody, spowodować jego wypłynięcie? Pole
powierzchni otworu wynosi
można, nalewająć do naczynia wody, spowodować jego wypłynięcie? Pole
powierzchni otworu wynosi
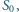 napięcie powierzchniowe wody można
zaniedbać.
napięcie powierzchniowe wody można
zaniedbać.
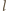 odległość wierzchołka stożka od dna naczynia.
Mamy wtedy
odległość wierzchołka stożka od dna naczynia.
Mamy wtedy
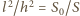 . Maksymalna siła wyporu działa, gdy poziom
wody sięga podstawy stożka. Stąd:
. Maksymalna siła wyporu działa, gdy poziom
wody sięga podstawy stożka. Stąd:
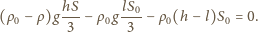
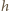 i
i
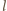 otrzymujemy:
otrzymujemy:
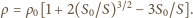
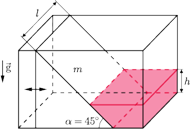
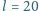 cm, masa
cm, masa
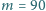 g, kąt przy wierzchołku wynosi
g, kąt przy wierzchołku wynosi
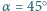 , a wysokość
słupa wody jest równa
, a wysokość
słupa wody jest równa
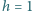 cm.
cm.