Klub 44F - zadania I 2015»Zadanie 591
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania I 2015
- Publikacja w Delcie: styczeń 2015
- Publikacja elektroniczna: 1 stycznia 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (93 KB)
Na sferze o promieniu 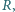 złożonej z dwóch półsfer, równomiernie rozłożony jest ładunek
złożonej z dwóch półsfer, równomiernie rozłożony jest ładunek 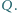 Jaką siłą trzeba działać na każdą półsferę, aby nie rozsuwały się one pod wpływem oddziaływania ładunków?
Jaką siłą trzeba działać na każdą półsferę, aby nie rozsuwały się one pod wpływem oddziaływania ładunków?
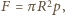 gdzie
gdzie 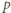 jest ciśnieniem wywieranym od wewnątrz na powierzchnię sfery, wywołanym oddziaływaniem ładunków. Aby wyznaczyć
jest ciśnieniem wywieranym od wewnątrz na powierzchnię sfery, wywołanym oddziaływaniem ładunków. Aby wyznaczyć 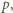 należy obliczyć pracę, jaką trzeba wykonać, zmniejszając promień sfery o małą wielkość
należy obliczyć pracę, jaką trzeba wykonać, zmniejszając promień sfery o małą wielkość 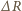 :
:![4-πp[R3-−-(R-−∆-R)3] 2 ∆W = p ∆ V = 3 ≈4 πR p ∆R.](/math/temat/fizyka/e_i_m/zadania/2014/12/28/zf-k44-591/5x-ea2d00b6e7ba9a495f7e052ea4a8cda665e28e15-dm-66,57,43-FF,FF,FF.gif)
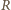 naładowanej ładunkiem
naładowanej ładunkiem 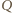 wynosi
wynosi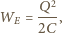
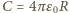 jest pojemnością sfery. Stąd
jest pojemnością sfery. Stąd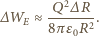
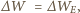 więc mamy
więc mamy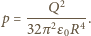
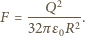
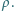 Walec obraca się ze stałą prędkością kątową
Walec obraca się ze stałą prędkością kątową 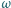 wokół własnej osi. Wewnątrz walca, wzdłuż jego promienia, umocowany jest cienki pręt
wokół własnej osi. Wewnątrz walca, wzdłuż jego promienia, umocowany jest cienki pręt 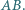 Po pręcie może ślizgać się bez tarcia koralik w kształcie kuli o masie
Po pręcie może ślizgać się bez tarcia koralik w kształcie kuli o masie  i promieniu
i promieniu 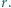 Kula połączona jest z końcem
Kula połączona jest z końcem 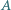 pręta za pomocą sprężyny o współczynniku sprężystości
pręta za pomocą sprężyny o współczynniku sprężystości 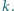 Długość nieodkształconej sprężyny wynosi
Długość nieodkształconej sprężyny wynosi 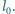 Znaleźć odległość środka kuli od osi obrotu.
Znaleźć odległość środka kuli od osi obrotu.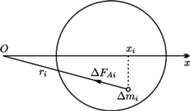
 szukaną odległość środka kuli od punktu
szukaną odległość środka kuli od punktu 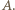 W układzie inercjalnym w kierunku wzdłuż pręta działają na kulę: siła sprężystości
W układzie inercjalnym w kierunku wzdłuż pręta działają na kulę: siła sprężystości 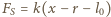 oraz siła ze strony cieczy
oraz siła ze strony cieczy 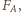 a ich wypadkowa jest siłą dośrodkową
a ich wypadkowa jest siłą dośrodkową 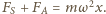 Aby wyznaczyć siłę
Aby wyznaczyć siłę 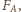 rozważmy obracające się naczynie z samą cieczą, wyodrębnijmy w niej myślowo część znajdującą się w tym samym miejscu co kula i podzielmy ją na bardzo małe elementy o masach
rozważmy obracające się naczynie z samą cieczą, wyodrębnijmy w niej myślowo część znajdującą się w tym samym miejscu co kula i podzielmy ją na bardzo małe elementy o masach 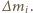 Siła ze strony pozostałej cieczy działająca na taki element w płaszczyźnie poziomej wynosi
Siła ze strony pozostałej cieczy działająca na taki element w płaszczyźnie poziomej wynosi 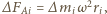 gdzie
gdzie 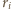 jest odległością elementu od osi obrotu. Niech pozioma oś
jest odległością elementu od osi obrotu. Niech pozioma oś 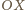 prostokątnego układu współrzędnych ma początek na osi obrotu i przechodzi przez środek wydzielonej części cieczy, a oś
prostokątnego układu współrzędnych ma początek na osi obrotu i przechodzi przez środek wydzielonej części cieczy, a oś 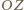 skierowana jest wzdłuż osi obrotu, prostopadle do płaszczyzny rysunku. Rzut siły
skierowana jest wzdłuż osi obrotu, prostopadle do płaszczyzny rysunku. Rzut siły 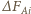 na oś
na oś 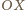 wynosi
wynosi 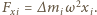 Całkowita siła działająca w płaszczyźnie poziomej ze strony pozostałej cieczy na część wyróżnioną działa wzdłuż osi
Całkowita siła działająca w płaszczyźnie poziomej ze strony pozostałej cieczy na część wyróżnioną działa wzdłuż osi 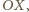 co wynika z symetrii problemu, skierowana jest do osi obrotu i ma wartość
co wynika z symetrii problemu, skierowana jest do osi obrotu i ma wartość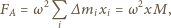
 jest odległością środka masy kuli od osi obrotu, a
jest odległością środka masy kuli od osi obrotu, a 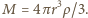 Siła
Siła 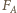 zależy tylko od położenia, kształtu i objętości wyróżnionej części cieczy. Taka sama siła działa na dowolne ciało umieszczone w tym samym miejscu wewnątrz cieczy. Szukana odległość wynosi
zależy tylko od położenia, kształtu i objętości wyróżnionej części cieczy. Taka sama siła działa na dowolne ciało umieszczone w tym samym miejscu wewnątrz cieczy. Szukana odległość wynosi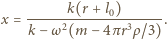
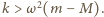 W przeciwnym przypadku sprężyna jest zbyt słaba, aby utrzymać kulę wewnątrz cieczy, i kula w zależności od swojej gęstości przemieszcza się do jednego z końców pręta.
W przeciwnym przypadku sprężyna jest zbyt słaba, aby utrzymać kulę wewnątrz cieczy, i kula w zależności od swojej gęstości przemieszcza się do jednego z końców pręta.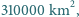 z czego około
z czego około 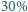 to lasy, ale tylko
to lasy, ale tylko 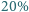 z nich to lasy liściaste. Najwyższy wiąz w Polsce ma 36 m wysokości (Komorów k. Gubina), najwyższa lipa 35 m (Cielętniki k. Częstochowy).
z nich to lasy liściaste. Najwyższy wiąz w Polsce ma 36 m wysokości (Komorów k. Gubina), najwyższa lipa 35 m (Cielętniki k. Częstochowy).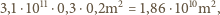
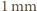 do
do 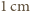 - przyjmijmy
- przyjmijmy 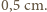 Gęstość liści jest bliska gęstości wody - przyjmijmy, że wynosi
Gęstość liści jest bliska gęstości wody - przyjmijmy, że wynosi 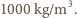 Jeśli najwyższe drzewa liściaste w Polsce osiągają wysokość około 35 m, to liście spadają z wysokości od 1 do 30 m - przyjmijmy średnio 10 m. Przyspieszenie ziemskie wynosi około
Jeśli najwyższe drzewa liściaste w Polsce osiągają wysokość około 35 m, to liście spadają z wysokości od 1 do 30 m - przyjmijmy średnio 10 m. Przyspieszenie ziemskie wynosi około 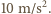 Ostatecznie otrzymujemy zmianę energii potencjalnej liści równą w przybliżeniu
Ostatecznie otrzymujemy zmianę energii potencjalnej liści równą w przybliżeniu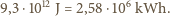
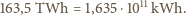
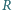 wirująca z prędkością kątową
wirująca z prędkością kątową 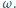 Pracownik wesołego miasteczka założył się z kolegami, że startując ze środka tarczy i idąc ze stałą prędkością wzdłuż wymalowanego na tarczy promienia dotrze do brzegu tarczy w chwili, gdy wykona ona połowę obrotu. Czy wygra zakład, jeśli współczynnik tarcia między powierzchnią tarczy i podeszwami butów pracownika wynosi
Pracownik wesołego miasteczka założył się z kolegami, że startując ze środka tarczy i idąc ze stałą prędkością wzdłuż wymalowanego na tarczy promienia dotrze do brzegu tarczy w chwili, gdy wykona ona połowę obrotu. Czy wygra zakład, jeśli współczynnik tarcia między powierzchnią tarczy i podeszwami butów pracownika wynosi 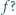
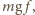 gdzie
gdzie  jest masą pracownika, a
jest masą pracownika, a 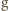 przyspieszeniem ziemskim, musi być przez cały czas ruchu nie mniejsza od wartości wypadkowej sumy sił: odśrodkowej i Coriolisa. Siła odśrodkowa i siła Coriolisa są do siebie prostopadłe i co do wartości odpowiednio równe
przyspieszeniem ziemskim, musi być przez cały czas ruchu nie mniejsza od wartości wypadkowej sumy sił: odśrodkowej i Coriolisa. Siła odśrodkowa i siła Coriolisa są do siebie prostopadłe i co do wartości odpowiednio równe 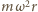 oraz
oraz 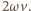 Prędkość pracownika (zgodna z warunkami zadania) to
Prędkość pracownika (zgodna z warunkami zadania) to 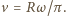
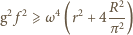
 pracownika od środka tarczy. Ostatecznie:
pracownika od środka tarczy. Ostatecznie: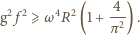

 Znaleźć przyspieszenie deski. Nie ma poślizgu między walcami i deską oraz między walcami i podłogą. Masy walców są zaniedbywalnie małe w porównaniu z masą deski.
Znaleźć przyspieszenie deski. Nie ma poślizgu między walcami i deską oraz między walcami i podłogą. Masy walców są zaniedbywalnie małe w porównaniu z masą deski.
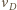 jest taka sama jak punktów na powierzchni walców, które w danej chwili stykają się z deską. Niech
jest taka sama jak punktów na powierzchni walców, które w danej chwili stykają się z deską. Niech 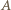 będzie jednym z takich punktów. Jego prędkość względem ziemi jest złożeniem poziomej prędkości ruchu postępowego walca
będzie jednym z takich punktów. Jego prędkość względem ziemi jest złożeniem poziomej prędkości ruchu postępowego walca  i prędkości ruchu obrotowego względem środka walca o tej samej wartości. Wektor prędkości deski względem ziemi tworzy z poziomem kąt
i prędkości ruchu obrotowego względem środka walca o tej samej wartości. Wektor prędkości deski względem ziemi tworzy z poziomem kąt 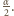 Tarcie jest statyczne, możemy więc korzystać z zasady zachowania energii mechanicznej, zaniedbując zmianę energii kinetycznej walców:
Tarcie jest statyczne, możemy więc korzystać z zasady zachowania energii mechanicznej, zaniedbując zmianę energii kinetycznej walców: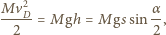
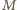 jest masą deski a
jest masą deski a 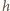 jej przesunięciem w kierunku pionowym. Droga
jej przesunięciem w kierunku pionowym. Droga  przebyta przez deskę od chwili rozpoczęcia ruchu dana jest wzorem
przebyta przez deskę od chwili rozpoczęcia ruchu dana jest wzorem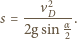
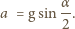
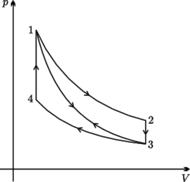
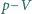 są przemianami izotermicznymi. Proces 1-3 jest przemianą adiabatyczną. Procesy 2-3 oraz 4-1 to izochory. Sprawność cyklu 1-2-3-1 wynosi
są przemianami izotermicznymi. Proces 1-3 jest przemianą adiabatyczną. Procesy 2-3 oraz 4-1 to izochory. Sprawność cyklu 1-2-3-1 wynosi 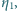 sprawność cyklu 1-3-4-1 wynosi
sprawność cyklu 1-3-4-1 wynosi 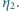 Oblicz sprawność cyklu 1-2-3-4-1.
Oblicz sprawność cyklu 1-2-3-4-1.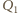 ciepło pobrane na izotermie 1-2, a przez
ciepło pobrane na izotermie 1-2, a przez 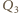 wartość bezwzględną ciepła oddanego na izotermie 3-4. Na wykresie
wartość bezwzględną ciepła oddanego na izotermie 3-4. Na wykresie 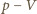 są one równe polu pod odpowiednią izotermą, bo w przemianie izotermicznej energia wewnętrzna nie zmienia się. Zatem praca uzyskana w cyklu 1-2-3-4-1 wynosi
są one równe polu pod odpowiednią izotermą, bo w przemianie izotermicznej energia wewnętrzna nie zmienia się. Zatem praca uzyskana w cyklu 1-2-3-4-1 wynosi 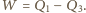 Sprawność tego cyklu
Sprawność tego cyklu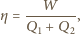
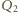 jest ciepłem pobranym na izochorze 4-1. Jest ono równe wartości bezwzględnej ciepła oddanego na izochorze 2-3, bo obie izochory łączą na wykresie
jest ciepłem pobranym na izochorze 4-1. Jest ono równe wartości bezwzględnej ciepła oddanego na izochorze 2-3, bo obie izochory łączą na wykresie 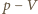 punkty o tych samych temperaturach. Sprawność cyklu 1-2-3-1 dana jest wzorem
punkty o tych samych temperaturach. Sprawność cyklu 1-2-3-1 dana jest wzorem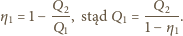
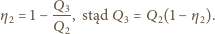
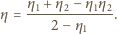

 zawieszono na nierozciągliwej, nieważkiej nici o długości
zawieszono na nierozciągliwej, nieważkiej nici o długości 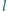 kulkę o masie
kulkę o masie  Kulkę wychylono w lewo o mały kąt
Kulkę wychylono w lewo o mały kąt 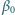 większy od
większy od 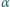 (
(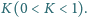 Jaki będzie maksymalny kąt dla kolejnych wychyleń kulki w lewo?
Jaki będzie maksymalny kąt dla kolejnych wychyleń kulki w lewo?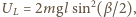 a w prawo
a w prawo 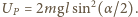 Dla małych kątów
Dla małych kątów 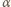 i
i 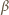 mamy:
mamy: 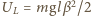 i
i 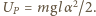 Po pierwszym uderzeniu w powierzchnię kulka będzie miała energię kinetyczną
Po pierwszym uderzeniu w powierzchnię kulka będzie miała energię kinetyczną 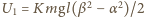 i wychyli się o kąt
i wychyli się o kąt 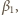 odpowiadający sumie tej energii kinetycznej i energii potencjalnej odpowiadającej wychyleniu o kąt
odpowiadający sumie tej energii kinetycznej i energii potencjalnej odpowiadającej wychyleniu o kąt 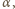 czyli
czyli 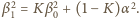 Powtarzając to rozumowanie dla kolejnych uderzeń, dostajemy ogólne wyrażenie na wartość kąta po
Powtarzając to rozumowanie dla kolejnych uderzeń, dostajemy ogólne wyrażenie na wartość kąta po  -tym uderzeniu:
-tym uderzeniu:  Zauważmy, że
Zauważmy, że 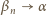 dla
dla 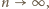 chyba że
chyba że 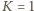 (zderzenie sprężyste), kiedy to
(zderzenie sprężyste), kiedy to 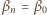 dla dowolnego
dla dowolnego 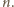
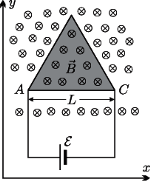
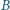 umieszczono cienką metalową płytkę, mającą kształt trójkąta równobocznego o boku
umieszczono cienką metalową płytkę, mającą kształt trójkąta równobocznego o boku 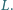 Grubość płytki wynosi
Grubość płytki wynosi 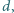 jej gęstość jest równa
jej gęstość jest równa 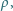 a jej powierzchnia jest prostopadła do kierunku pola magnetycznego. Do wierzchołków
a jej powierzchnia jest prostopadła do kierunku pola magnetycznego. Do wierzchołków 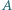 i
i 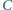 trójkąta dołączono źródło napięcia o sile elektromotorycznej
trójkąta dołączono źródło napięcia o sile elektromotorycznej 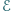 i oporności wewnętrznej
i oporności wewnętrznej 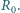 Znaleźć przyspieszenie płytki. Zaniedbać masę, oporność i sprężystość łączących przewodów oraz oporność płytki.
Znaleźć przyspieszenie płytki. Zaniedbać masę, oporność i sprężystość łączących przewodów oraz oporność płytki.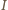 płynącego wzdłuż krzywej
płynącego wzdłuż krzywej 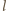 siła elektrodynamiczna działająca na element prądu
siła elektrodynamiczna działająca na element prądu 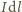 jest dana iloczynem wektorowym
jest dana iloczynem wektorowym 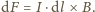 Ze względu na kształt rozważanego obwodu elektrycznego sumy składowych elementów prądu o zwrocie
Ze względu na kształt rozważanego obwodu elektrycznego sumy składowych elementów prądu o zwrocie 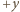 i
i 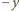 muszą mieć taką samą wartość, a w konsekwencji składowa
muszą mieć taką samą wartość, a w konsekwencji składowa  wypadkowej siły elektrodynamicznej wyniesie zero. Natomiast suma wszystkich składowych
wypadkowej siły elektrodynamicznej wyniesie zero. Natomiast suma wszystkich składowych 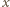 elementów prądu musi być skierowana od
elementów prądu musi być skierowana od 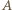 do
do 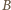 i musi być równa całkowitemu prądowi, przepływającemu przez płytkę, a długość składowej
i musi być równa całkowitemu prądowi, przepływającemu przez płytkę, a długość składowej  dowolnej drogi przepływu prądu musi być równa
dowolnej drogi przepływu prądu musi być równa 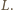 Stąd siła działająca na płytkę to
Stąd siła działająca na płytkę to 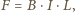 gdzie prąd
gdzie prąd 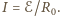 Masa płytki wynosi
Masa płytki wynosi 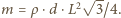 Z II zasady dynamiki dostajemy
Z II zasady dynamiki dostajemy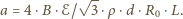
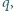 okazało się, że cząstka i kula przyciągają się z siłą
okazało się, że cząstka i kula przyciągają się z siłą 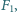 gdy naładowano kulę ładunkiem
gdy naładowano kulę ładunkiem 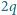 - cząstka i kula przyciągają się z siłą
- cząstka i kula przyciągają się z siłą 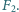 Jak duża będzie siła działająca pomiędzy cząstką i kulą, gdy ta ostatnia zostanie naładowana ładunkiem
Jak duża będzie siła działająca pomiędzy cząstką i kulą, gdy ta ostatnia zostanie naładowana ładunkiem 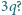
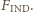 Jeżeli ładujemy kulę kolejno ładunkiem
Jeżeli ładujemy kulę kolejno ładunkiem 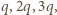 to pojawia się dodatkowa siła odpychania odpowiednio
to pojawia się dodatkowa siła odpychania odpowiednio 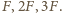 Znajdując wypadkową siłę działającą pomiędzy kulą i cząstką, w każdym z tych przypadków, dostajemy
Znajdując wypadkową siłę działającą pomiędzy kulą i cząstką, w każdym z tych przypadków, dostajemy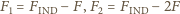
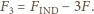
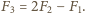 Zauważmy, że siła ta może być siłą przyciągania albo odpychania.
Zauważmy, że siła ta może być siłą przyciągania albo odpychania.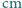 wypełniono całkowicie wodą i umieszczono w pokoju, w którym nie ma prądów powietrza. Przez dwie doby poziom wody w akwarium obniżył się o 1 centymetr. Przyjmując, że temperatura i wilgotność powietrza w pokoju są stałe, a proces parowania jest na tyle powolny, że temperatura wody nie ulega zmianie, znaleźć czas, po którym woda całkowicie wyparuje z akwarium.
wypełniono całkowicie wodą i umieszczono w pokoju, w którym nie ma prądów powietrza. Przez dwie doby poziom wody w akwarium obniżył się o 1 centymetr. Przyjmując, że temperatura i wilgotność powietrza w pokoju są stałe, a proces parowania jest na tyle powolny, że temperatura wody nie ulega zmianie, znaleźć czas, po którym woda całkowicie wyparuje z akwarium.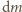 parująca w bardzo krótkim czasie
parująca w bardzo krótkim czasie 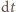 jest proporcjonalna do pola powierzchni wody
jest proporcjonalna do pola powierzchni wody 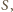 czyli
czyli 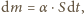 gdzie
gdzie 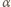 jest współczynnikiem proporcjonalności. Zmiana poziomu wody w akwarium
jest współczynnikiem proporcjonalności. Zmiana poziomu wody w akwarium 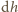 wiąże się ze zmianą jej masy zależnością
wiąże się ze zmianą jej masy zależnością 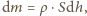 gdzie
gdzie 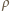 - gęstość wody. Stąd
- gęstość wody. Stąd 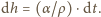 Tak więc w stałych warunkach parowania zmiana poziomu wody jest proporcjonalna do czasu. Jeżeli więc przez dwie doby poziom wody obniżył się o 1 centymetr, to cała woda, przy głębokości akwarium równej 15
Tak więc w stałych warunkach parowania zmiana poziomu wody jest proporcjonalna do czasu. Jeżeli więc przez dwie doby poziom wody obniżył się o 1 centymetr, to cała woda, przy głębokości akwarium równej 15 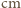 , wyparuje po 30 dobach.
, wyparuje po 30 dobach.
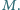 Do końca nici przyłożono poziomą siłę
Do końca nici przyłożono poziomą siłę 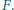 Z jakim przyspieszeniem porusza się ten koniec nici? Załóż brak tarcia i przyjmij, że klocki poruszają się ruchem postępowym.
Z jakim przyspieszeniem porusza się ten koniec nici? Załóż brak tarcia i przyjmij, że klocki poruszają się ruchem postępowym.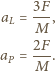
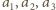 wartości bezwzględne przyspieszeń względem ziemi poziomych odcinków nici, od najniższego do najwyższego. Mamy wtedy:
wartości bezwzględne przyspieszeń względem ziemi poziomych odcinków nici, od najniższego do najwyższego. Mamy wtedy: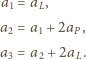
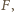 wynosi
wynosi 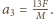
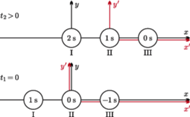
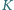 i
i 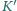 to inercjalne układy odniesienia o zgodnych osiach,
to inercjalne układy odniesienia o zgodnych osiach, 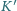 porusza się z prędkością
porusza się z prędkością 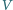 względem
względem 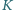 wzdłuż osi
wzdłuż osi  Wzdłuż tej osi w układzie
Wzdłuż tej osi w układzie 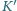 rozmieszczony jest ciąg jednakowych, równo odległych i zsynchronizowanych zegarów. Obserwator w
rozmieszczony jest ciąg jednakowych, równo odległych i zsynchronizowanych zegarów. Obserwator w 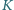 notuje równoczesne dla niego wskazania tych zegarów w dwóch chwilach:
notuje równoczesne dla niego wskazania tych zegarów w dwóch chwilach: 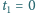 i
i 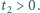 Na podstawie tych pomiarów wyznaczyć
Na podstawie tych pomiarów wyznaczyć 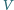 oraz odległość
oraz odległość 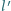 między sąsiednimi zegarami mierzoną w
między sąsiednimi zegarami mierzoną w 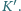
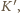 zatem
zatem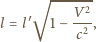
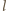 jest odległością między sąsiednimi zegarami w układzie
jest odległością między sąsiednimi zegarami w układzie 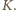 W czasie
W czasie 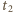 każdy z zegarów przebywa w tym układzie drogę
każdy z zegarów przebywa w tym układzie drogę 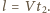 Po upływie czasu
Po upływie czasu 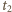 wskazania tych samych zegarów w
wskazania tych samych zegarów w 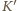 różnią się o
różnią się o 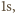 stąd
stąd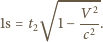
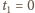 współrzędna przestrzenna trzeciego zegara w układzie
współrzędna przestrzenna trzeciego zegara w układzie 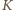 wynosi
wynosi 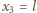 i zegar ten wskazuje czas
i zegar ten wskazuje czas 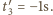 Zgodnie z transformacją Lorentza:
Zgodnie z transformacją Lorentza: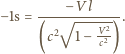
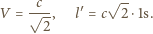

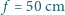 usunięto część środkową o szerokości
usunięto część środkową o szerokości 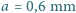 . Obie połówki soczewki stykają się. Średnica soczewki wynosi
. Obie połówki soczewki stykają się. Średnica soczewki wynosi 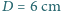 . W odległości
. W odległości 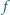 od soczewki, na jej osi optycznej, ustawiono punktowe źródło światła monochromatycznego o długości fali
od soczewki, na jej osi optycznej, ustawiono punktowe źródło światła monochromatycznego o długości fali 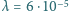 m. Z drugiej strony soczewki umieszczony jest ekran. Jakie musi być położenie ekranu, aby można było obserwować na nim prążki interferencyjne? Zakładając, że warunek ten jest spełniony, znaleźć odległość między sąsiednimi jasnymi prążkami.
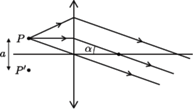
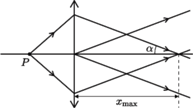
m. Z drugiej strony soczewki umieszczony jest ekran. Jakie musi być położenie ekranu, aby można było obserwować na nim prążki interferencyjne? Zakładając, że warunek ten jest spełniony, znaleźć odległość między sąsiednimi jasnymi prążkami.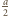 od ogniska umieścimy punkt świecący
od ogniska umieścimy punkt świecący 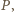 to promienie wychodzące z tego punktu po przejściu przez soczewkę utworzą wiązkę równoległą nachyloną do osi optycznej soczewki pod kątem
to promienie wychodzące z tego punktu po przejściu przez soczewkę utworzą wiązkę równoległą nachyloną do osi optycznej soczewki pod kątem 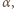 przy czym
przy czym 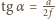 (
(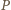 tworzą przecinające się wiązki równoległe. Z
tworzą przecinające się wiązki równoległe. Z 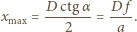
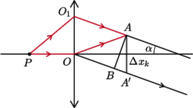
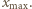 Na środku ekranu powstaje maksimum interferencyjne. Aby w p.
Na środku ekranu powstaje maksimum interferencyjne. Aby w p. 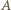 w odległości
w odległości 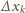 od środka ekranu powstało
od środka ekranu powstało 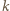 -te maksimum (
-te maksimum (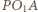 i
i 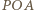 muszą się wzmacniać, zatem ich różnica dróg optycznych wynosi
muszą się wzmacniać, zatem ich różnica dróg optycznych wynosi 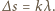 Droga optyczna promienia
Droga optyczna promienia 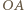 jest taka sama jak promienia
jest taka sama jak promienia 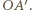 Promienie z wiązki równoległej mają w punktach
Promienie z wiązki równoległej mają w punktach 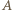 i
i 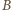 zgodne fazy, zatem
zgodne fazy, zatem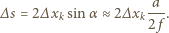
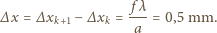

 jednorodny klocek o długości
jednorodny klocek o długości 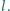 Klocek wsuwa się na szorstki odcinek powierzchni o współczynniku tarcia
Klocek wsuwa się na szorstki odcinek powierzchni o współczynniku tarcia 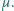 Po jakim czasie klocek zatrzyma się?
Po jakim czasie klocek zatrzyma się?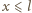 oznacza odległość, na jaką wsunął się na szorstką powierzchnię poruszający się klocek. Działa na niego siła tarcia
oznacza odległość, na jaką wsunął się na szorstką powierzchnię poruszający się klocek. Działa na niego siła tarcia 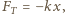 gdzie
gdzie 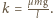 Klocek będzie się poruszał ruchem harmonicznym do chwili, kiedy albo zatrzyma się, albo cały wjedzie na szorstką powierzchnię. Z zasady zachowania energii możemy wyznaczyć amplitudę drgań
Klocek będzie się poruszał ruchem harmonicznym do chwili, kiedy albo zatrzyma się, albo cały wjedzie na szorstką powierzchnię. Z zasady zachowania energii możemy wyznaczyć amplitudę drgań 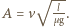
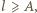 czyli długość klocka jest nie mniejsza od amplitudy drgań, a stąd
czyli długość klocka jest nie mniejsza od amplitudy drgań, a stąd 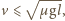 klocek zatrzyma się po czasie
klocek zatrzyma się po czasie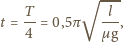
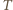 jest okresem drgań.
jest okresem drgań.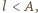 klocek wjedzie na szorstką powierzchnię w czasie
klocek wjedzie na szorstką powierzchnię w czasie 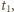 poruszając się ruchem harmonicznym, a następnie w czasie
poruszając się ruchem harmonicznym, a następnie w czasie 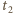 będzie poruszał się ruchem jednostajnie opóźnionym. Droga przebyta ruchem harmonicznym
będzie poruszał się ruchem jednostajnie opóźnionym. Droga przebyta ruchem harmonicznym 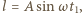 gdzie
gdzie 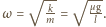 Prędkość
Prędkość 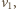 jaką osiągnie klocek w chwili
jaką osiągnie klocek w chwili 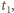 możemy otrzymać z zasady zachowania energii:
możemy otrzymać z zasady zachowania energii: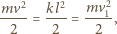
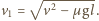 Ruch jednostajnie opóźniony odbywać się będzie w czasie
Ruch jednostajnie opóźniony odbywać się będzie w czasie 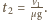 Klocek zatrzyma się po czasie
Klocek zatrzyma się po czasie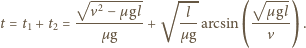
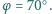 Niestety, nieostrożne spalanie paliw kopalnych przez mieszkańców okolic o umiarkowanym klimacie spowodowało wzrost temperatury atmosfery (tzw. efekt cieplarniany) i stopienie obu okołobiegunowych lądolodów. O ile zmieniła się długość doby jeśli początkowo doba trwała
Niestety, nieostrożne spalanie paliw kopalnych przez mieszkańców okolic o umiarkowanym klimacie spowodowało wzrost temperatury atmosfery (tzw. efekt cieplarniany) i stopienie obu okołobiegunowych lądolodów. O ile zmieniła się długość doby jeśli początkowo doba trwała 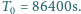 Masa planety wynosi
Masa planety wynosi 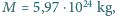 jej promień
jej promień 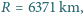 a masa lądolodów
a masa lądolodów 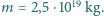 Załóż, że planeta jest niemal idealną kulą.
Załóż, że planeta jest niemal idealną kulą.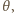 promieniu
promieniu  i masie
i masie  wynosi
wynosi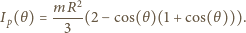
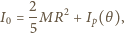
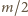 i kącie
i kącie 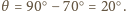 Po stopnieniu lodu woda pokryje całą powierzchnię planety - dla uproszczenia obliczeń przyjmijmy, że tworzy na niej warstwę o grubości niezależnej od szerokości geograficznej. Końcowy moment bezwładności planety wynosi więc
Po stopnieniu lodu woda pokryje całą powierzchnię planety - dla uproszczenia obliczeń przyjmijmy, że tworzy na niej warstwę o grubości niezależnej od szerokości geograficznej. Końcowy moment bezwładności planety wynosi więc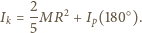
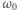 na
na 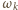 zgodnie z zasada zachowania momentu pędu:
zgodnie z zasada zachowania momentu pędu: 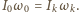 Ostatecznie otrzymujemy:
Ostatecznie otrzymujemy: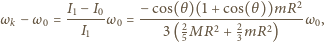
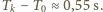
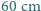 . Jaki jest największy promień skalnej planetoidy, od której przyciągania człowiek mógłby uwolnić się o własnych siłach? Średni promień Ziemi wynosi
. Jaki jest największy promień skalnej planetoidy, od której przyciągania człowiek mógłby uwolnić się o własnych siłach? Średni promień Ziemi wynosi 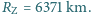 Przyjmij, że średnia gęstość planetoidy jest równa średniej gęstości Ziemi.
Przyjmij, że średnia gęstość planetoidy jest równa średniej gęstości Ziemi. na wysokość
na wysokość 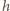 wymaga wykonania pracy
wymaga wykonania pracy 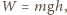 gdzie
gdzie 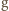 oznacza przyspieszenie spadku swobodnego na powierzchni Ziemi. Uwolnienie się od przyciągania planetoidy o masie
oznacza przyspieszenie spadku swobodnego na powierzchni Ziemi. Uwolnienie się od przyciągania planetoidy o masie 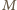 i promieniu
i promieniu 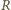 wymaga wykonania pracy równej energii "wiązania grawitacyjnego"
wymaga wykonania pracy równej energii "wiązania grawitacyjnego" 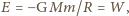 gdzie
gdzie 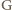 oznacza stałą grawitacji. Biorąc pod uwagę, że
oznacza stałą grawitacji. Biorąc pod uwagę, że 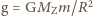 oraz związek masy kuli z jej promieniem i gęstością otrzymujemy ostatecznie
oraz związek masy kuli z jej promieniem i gęstością otrzymujemy ostatecznie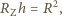
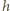 i
i 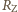 daje
daje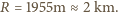
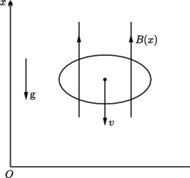
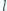 i oporze
i oporze 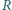 spada pod działaniem siły ciężkości w polu magnetycznym. Wartość wektora indukcji magnetycznej w kierunku pionowym zmienia się z wysokością zgodnie ze wzorem
spada pod działaniem siły ciężkości w polu magnetycznym. Wartość wektora indukcji magnetycznej w kierunku pionowym zmienia się z wysokością zgodnie ze wzorem
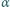 jest dodatnia. Znaleźć zależność siły hamującej ruch pierścienia od jego prędkości. Płaszczyzna pierścienia pozostaje prostopadła do linii pola magnetycznego.
jest dodatnia. Znaleźć zależność siły hamującej ruch pierścienia od jego prędkości. Płaszczyzna pierścienia pozostaje prostopadła do linii pola magnetycznego.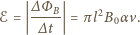
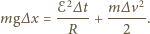
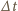 mamy:
mamy: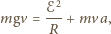
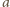 jest przyspieszeniem pierścienia. Równanie ruchu pierścienia ma postać:
jest przyspieszeniem pierścienia. Równanie ruchu pierścienia ma postać: 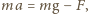 gdzie
gdzie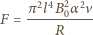
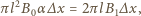
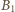 jest poziomą składową pola magnetycznego, prostopadłą do pierścienia. Siła elektrodynamiczna hamująca pierścień to
jest poziomą składową pola magnetycznego, prostopadłą do pierścienia. Siła elektrodynamiczna hamująca pierścień to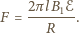
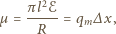
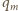 jest ładunkiem magnetycznym dipola. Siła hamująca wynosi
jest ładunkiem magnetycznym dipola. Siła hamująca wynosi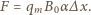
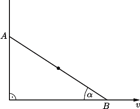
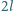 przyczepiona jest mała kulka o masie
przyczepiona jest mała kulka o masie  Pręt porusza się jak na rysunku. Koniec
Pręt porusza się jak na rysunku. Koniec 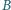 pręta porusza się w kierunku poziomym ze stałą prędkością
pręta porusza się w kierunku poziomym ze stałą prędkością 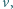 koniec
koniec 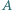 porusza się wzdłuż pionowej ściany. Jaką siłę reakcji wywiera pręt na kulkę, gdy tworzy z poziomem kąt
porusza się wzdłuż pionowej ściany. Jaką siłę reakcji wywiera pręt na kulkę, gdy tworzy z poziomem kąt 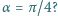

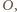 bo znajduje się w połowie przeciwprostokątnej trójkąta
bo znajduje się w połowie przeciwprostokątnej trójkąta 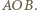 Gdy
Gdy 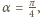 prędkość kulki jest skierowana wzdłuż pręta i ma wartość
prędkość kulki jest skierowana wzdłuż pręta i ma wartość 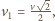 bo wszystkie punkty sztywnego pręta mają taką samą składową prędkości wzdłuż pręta. Oznaczając przez
bo wszystkie punkty sztywnego pręta mają taką samą składową prędkości wzdłuż pręta. Oznaczając przez 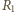 składową siły reakcji prostopadłą do pręta i przyjmując, że ma ona zwrot jak na rysunku, możemy napisać wzór na siłę dośrodkową:
składową siły reakcji prostopadłą do pręta i przyjmując, że ma ona zwrot jak na rysunku, możemy napisać wzór na siłę dośrodkową: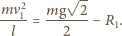
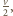 bo przebywa drogę dwukrotnie mniejszą niż koniec pręta
bo przebywa drogę dwukrotnie mniejszą niż koniec pręta 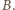 Zatem przyspieszenie kulki oraz wypadkowa siła reakcji mają kierunek pionowy. Wartość siły reakcji wynosi:
Zatem przyspieszenie kulki oraz wypadkowa siła reakcji mają kierunek pionowy. Wartość siły reakcji wynosi: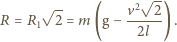
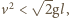 siła ta zwrócona jest do góry.
siła ta zwrócona jest do góry.
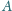 i
i
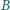 półnieskończonego
obwodu, jeżeli oporność każdego z jego elementów wynosi
półnieskończonego
obwodu, jeżeli oporność każdego z jego elementów wynosi
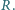
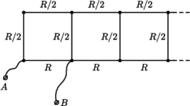
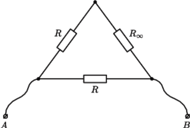
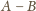 wynika, że potencjały
punktów symetrycznych względem tej linii są jednakowe. Na tej podstawie
możemy rozpatrywany obwód zastąpić obwodem, który z kolei można
zwinąć do postaci z rysunku 2 i znaleźć oporność pomiędzy
punktami
wynika, że potencjały
punktów symetrycznych względem tej linii są jednakowe. Na tej podstawie
możemy rozpatrywany obwód zastąpić obwodem, który z kolei można
zwinąć do postaci z rysunku 2 i znaleźć oporność pomiędzy
punktami
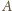 i
i
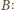
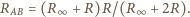
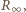 korzystamy z faktu, że oporność nieskończonego
obwodu jest taka sama z pierwszym jego ogniwem i bez niego. Stąd
korzystamy z faktu, że oporność nieskończonego
obwodu jest taka sama z pierwszym jego ogniwem i bez niego. Stąd
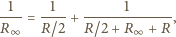
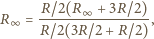
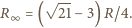
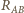 znajdujemy
znajdujemy
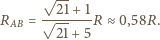
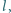 współczynniku
sprężystości
współczynniku
sprężystości
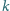 i masie
i masie
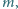 której końce połączono,
wiruje z prędkością kątową
której końce połączono,
wiruje z prędkością kątową
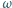 wokół osi prostopadłej do jego
płaszczyzny i przechodzącej przez jego środek. Jak zależy promień
kółka
wokół osi prostopadłej do jego
płaszczyzny i przechodzącej przez jego środek. Jak zależy promień
kółka
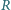 od prędkości
od prędkości
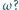 Przyjąć, że średnica zwojów
sprężyny jest dużo mniejsza od jej długości.
Przyjąć, że średnica zwojów
sprężyny jest dużo mniejsza od jej długości.
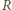 zrobionego ze sprężyny
przy prędkości kątowej
zrobionego ze sprężyny
przy prędkości kątowej
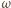 porusza się z przyspieszeniem
dośrodkowym
porusza się z przyspieszeniem
dośrodkowym
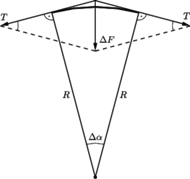
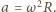 Jeśli przez
Jeśli przez
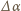 oznaczyć kąt pomiędzy
promieniami łączącymi końce tego elementu z położeniem osi obrotu, to jego
masę można zapisać jako
oznaczyć kąt pomiędzy
promieniami łączącymi końce tego elementu z położeniem osi obrotu, to jego
masę można zapisać jako
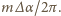 Siła dośrodkowa działająca
na ten element wynosi
Siła dośrodkowa działająca
na ten element wynosi
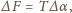 pochodzi od naciągu sprężyny
pochodzi od naciągu sprężyny
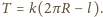
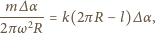
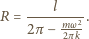
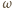 rośnie,
rośnie,
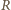 także rośnie, dążąc do wartości
maksymalnej, którą osiąga dla krytycznej wartości prędkości kątowej
także rośnie, dążąc do wartości
maksymalnej, którą osiąga dla krytycznej wartości prędkości kątowej
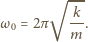
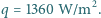 Jaki jest stosunek siły odpychającej Ziemię od Słońca
wynikającej z wywieranego przez to promieniowanie ciśnienia do siły
grawitacyjnego przyciągania Ziemi i Słońca?
Jaki jest stosunek siły odpychającej Ziemię od Słońca
wynikającej z wywieranego przez to promieniowanie ciśnienia do siły
grawitacyjnego przyciągania Ziemi i Słońca?
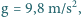 prędkość
światła
prędkość
światła
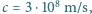 odległość Ziemia-Słońce to średnio
odległość Ziemia-Słońce to średnio
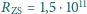 m, rok trwa w przybliżeniu
m, rok trwa w przybliżeniu
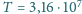 s, stała
grawitacji
s, stała
grawitacji
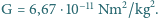
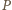 wynosi
wynosi
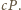 W związku z tym
pochłanianie przez Ziemię promieniowania słonecznego związane jest
z pochłanianiem strumienia pędu równego
W związku z tym
pochłanianie przez Ziemię promieniowania słonecznego związane jest
z pochłanianiem strumienia pędu równego
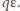 Związane
z pochłanianiem pędu promieniowania siła
Związane
z pochłanianiem pędu promieniowania siła
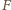 odpychająca od Słońca
Ziemię o promieniu
odpychająca od Słońca
Ziemię o promieniu
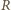 wynosi więc
wynosi więc
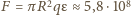 N. Siła
N. Siła
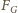 przyciągania Ziemi i Słońca wynosi:
przyciągania Ziemi i Słońca wynosi:
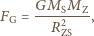
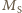 oznacza masę Słońca, a
oznacza masę Słońca, a
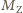 masę Ziemi. Przyspieszenie
Ziemi w ruchu dookoła Słońca wynosi
masę Ziemi. Przyspieszenie
Ziemi w ruchu dookoła Słońca wynosi
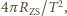 a masę Ziemi
możemy zastąpić wyrażeniem
a masę Ziemi
możemy zastąpić wyrażeniem
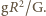 Po podstawieniu tych
wielkości otrzymujemy, że stosunek siły z jaką promieniowanie Słońca
odpycha Ziemię do siły przyciągania Ziemia-Słońce wynosi:
Po podstawieniu tych
wielkości otrzymujemy, że stosunek siły z jaką promieniowanie Słońca
odpycha Ziemię do siły przyciągania Ziemia-Słońce wynosi:
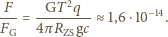
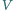 i ściankach doskonale odbijających
promieniowanie elektromagnetyczne wypełnione jest promieniowaniem
o całkowitej energii
i ściankach doskonale odbijających
promieniowanie elektromagnetyczne wypełnione jest promieniowaniem
o całkowitej energii
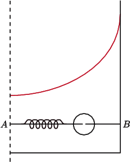
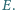 Jakie ciśnienie
Jakie ciśnienie
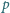 na ścianki naczynia
wywiera zawarte w nim promieniowanie elektromagnetyczne?
na ścianki naczynia
wywiera zawarte w nim promieniowanie elektromagnetyczne?
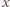 oznacza kierunek prostopadły do ścianki,
oznacza kierunek prostopadły do ścianki,
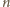 gęstość
fotonów, a
gęstość
fotonów, a
 średnią energię fotonu. Zderzając się sprężyście ze
ścianką foton o pędzie
średnią energię fotonu. Zderzając się sprężyście ze
ścianką foton o pędzie
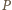 padający pod kątem
padający pod kątem
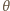 przekazuje jej
pęd
przekazuje jej
pęd
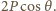 W jednostce czasu
W jednostce czasu
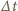 z każdego kierunku
tworzącego kąt
z każdego kierunku
tworzącego kąt
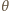 z normalną do każdego elementu ścianki
o powierzchni
z normalną do każdego elementu ścianki
o powierzchni
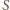 dolatuje więc
dolatuje więc
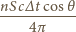
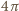 w mianowniku). Biorąc pod uwagę, że dla fotonu
w mianowniku). Biorąc pod uwagę, że dla fotonu
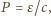 gdzie
gdzie
 jest prędkością światła, siła nacisku na ściankę
równa jest przekazowi pędu w jednostce czasu, a ciśnienie jest stosunkiem siły
nacisku do pola powierzchni, i sumując po wszystkich kątach padania,
otrzymujemy:
jest prędkością światła, siła nacisku na ściankę
równa jest przekazowi pędu w jednostce czasu, a ciśnienie jest stosunkiem siły
nacisku do pola powierzchni, i sumując po wszystkich kątach padania,
otrzymujemy:
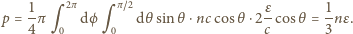
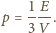
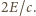
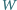 jest zamknięty i płynie prąd stały. Jaka ilość ciepła
wydzieli się w oporze
jest zamknięty i płynie prąd stały. Jaka ilość ciepła
wydzieli się w oporze
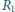 po otwarciu wyłącznika? Indukcyjność
cewki wynosi
po otwarciu wyłącznika? Indukcyjność
cewki wynosi
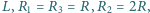 siła elektromotoryczna źródła
wynosi
siła elektromotoryczna źródła
wynosi
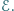 Oporność cewki oraz oporność wewnętrzna źródła
są zaniedbywalne.
Oporność cewki oraz oporność wewnętrzna źródła
są zaniedbywalne.
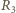 i cewkę, płynie
prąd
i cewkę, płynie
prąd
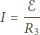
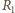 i
i
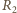 prąd nie płynie, bo spadek napięcia
na cewce jest równy zeru). Po otwarciu wyłącznika energia elektryczna
zgromadzona w cewce wydziela się w postaci ciepła
prąd nie płynie, bo spadek napięcia
na cewce jest równy zeru). Po otwarciu wyłącznika energia elektryczna
zgromadzona w cewce wydziela się w postaci ciepła
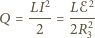
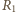 i
i
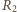 (przez opór
(przez opór
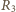 prąd nie płynie).
prąd nie płynie).
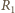 i
i
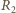 są połączone równolegle, więc spadki napięcia
na nich są równe
są połączone równolegle, więc spadki napięcia
na nich są równe
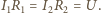 Ilość ciepła, jaka wydzieli się
w każdym z nich w ciągu krótkiego czasu
Ilość ciepła, jaka wydzieli się
w każdym z nich w ciągu krótkiego czasu
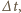 będzie równa
odpowiednio
będzie równa
odpowiednio
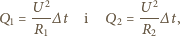
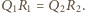 Równocześnie
Równocześnie
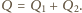 Ostatecznie
więc
Ostatecznie
więc
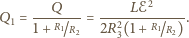
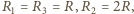 otrzymujemy
ostatecznie:
otrzymujemy
ostatecznie:
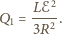
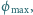 do jakiego może naładować
się oddalona od innych ciał miedziana kulka oświetlona światłem
ultrafioletowym o długości fali
do jakiego może naładować
się oddalona od innych ciał miedziana kulka oświetlona światłem
ultrafioletowym o długości fali
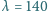 nm. Praca wyjścia dla miedzi
wynosi
nm. Praca wyjścia dla miedzi
wynosi
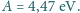
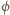 można wyrazić poprzez jej ładunek
można wyrazić poprzez jej ładunek
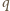 zależnością
zależnością
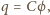 gdzie
gdzie
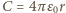 jest pojemnością kulki. Maksymalny
potencjał kulki
jest pojemnością kulki. Maksymalny
potencjał kulki
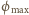 zależy od początkowej energii kinetycznej
elektronów. Ponieważ zmiana energii kinetycznej elektronów jest równa pracy
sił pola wytwarzanego przez kulkę, to przyjmując, że w nieskończoności
potencjał pola kulki i prędkość elektronu wynoszą zero i uwzględniając fakt,
że ładunek elektronu jest ujemny, można napisać:
zależy od początkowej energii kinetycznej
elektronów. Ponieważ zmiana energii kinetycznej elektronów jest równa pracy
sił pola wytwarzanego przez kulkę, to przyjmując, że w nieskończoności
potencjał pola kulki i prędkość elektronu wynoszą zero i uwzględniając fakt,
że ładunek elektronu jest ujemny, można napisać:
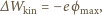
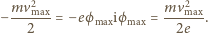
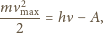
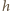 to stała Plancka,
to stała Plancka,
 – częstość światła. Podstawiając (2)
do (1), dostajemy
– częstość światła. Podstawiając (2)
do (1), dostajemy
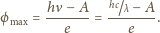
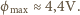
 i oporze właściwym
i oporze właściwym 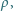 płynie prąd
płynie prąd 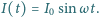 Znaleźć amplitudę napięcia na kondensatorze. Powierzchnia okładek kondensatora wynosi
Znaleźć amplitudę napięcia na kondensatorze. Powierzchnia okładek kondensatora wynosi 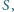 odległość między okładkami jest równa
odległość między okładkami jest równa 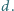

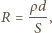 przez który płynie prąd o natężeniu
przez który płynie prąd o natężeniu 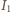 i kondensatora o pojemności
i kondensatora o pojemności 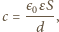 przez który płynie prąd o natężeniu
przez który płynie prąd o natężeniu 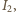 przy czym
przy czym 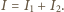 Napięcia na oporniku i kondensatorze są jednakowe:
Napięcia na oporniku i kondensatorze są jednakowe: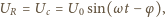
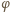 jest przesunięciem fazowym między napięciem i natężeniem prądu całkowitego
jest przesunięciem fazowym między napięciem i natężeniem prądu całkowitego 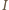 a
a 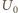 szukaną amplitudą napięcia. Ładunek na kondensatorze wynosi
szukaną amplitudą napięcia. Ładunek na kondensatorze wynosi 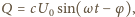 stąd
stąd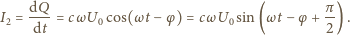
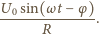
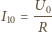 oraz
oraz 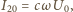 które tworzą ze sobą kąt
które tworzą ze sobą kąt  i obracają się wokół wspólnego punktu zaczepienia z prędkością kątową
i obracają się wokół wspólnego punktu zaczepienia z prędkością kątową 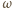 tak, że ich rzuty na wyróżnioną oś wynoszą
tak, że ich rzuty na wyróżnioną oś wynoszą 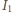 oraz
oraz 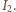 Wtedy wektor będący ich sumą wektorową ma długość
Wtedy wektor będący ich sumą wektorową ma długość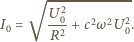
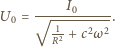
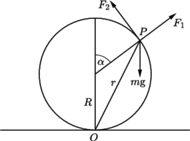
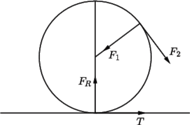
 działa siła ciężkości
działa siła ciężkości 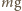 oraz siła reakcji sfery, której składowe wzdłuż promienia sfery i prostopadłą do promienia oznaczyliśmy przez
oraz siła reakcji sfery, której składowe wzdłuż promienia sfery i prostopadłą do promienia oznaczyliśmy przez 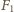 i
i 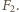
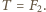 Gdy koralik przestaje naciskać na sferę znika siła tarcia
Gdy koralik przestaje naciskać na sferę znika siła tarcia 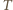 i z pierwszego warunku znikają wszystkie siły działające na sferę. Dopóki sfera toczy się bez poślizgu, ruch koralika możemy traktować jako czysty obrót wokół chwilowego środka w punkcie
i z pierwszego warunku znikają wszystkie siły działające na sferę. Dopóki sfera toczy się bez poślizgu, ruch koralika możemy traktować jako czysty obrót wokół chwilowego środka w punkcie 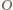 styczności sfery z podstawką. Wypadkowa sił działających na koralik jest siłą dośrodkową i w chwili, gdy rozpoczyna się poślizg równa jest składowej siły ciężkości wzdłuż odcinka
styczności sfery z podstawką. Wypadkowa sił działających na koralik jest siłą dośrodkową i w chwili, gdy rozpoczyna się poślizg równa jest składowej siły ciężkości wzdłuż odcinka 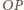 :
: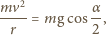
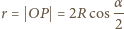 (
( 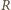 jest promieniem sfery). Jedyną siłą zewnętrzną działającą na układ, która wykonuje pracę, jest siła ciężkości działająca na koralik, z zasady zachowania energii mamy więc:
jest promieniem sfery). Jedyną siłą zewnętrzną działającą na układ, która wykonuje pracę, jest siła ciężkości działająca na koralik, z zasady zachowania energii mamy więc: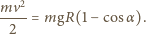
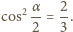 Koralik znajduje się wtedy na wysokości
Koralik znajduje się wtedy na wysokości 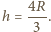 Od tej chwili koralik porusza się tylko pod działaniem siły ciężkości, czyli po paraboli, do momentu uderzenia w podstawkę. Sfera ślizga się po podstawce obracając się jednocześnie wokół własnej osi.
Od tej chwili koralik porusza się tylko pod działaniem siły ciężkości, czyli po paraboli, do momentu uderzenia w podstawkę. Sfera ślizga się po podstawce obracając się jednocześnie wokół własnej osi.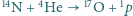 może zachodzić, gdy energia kinetyczna cząstek
może zachodzić, gdy energia kinetyczna cząstek  padających na nieruchome jądra azotu przewyższa energię progową
padających na nieruchome jądra azotu przewyższa energię progową 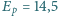 MeV. O ile energia kinetyczna cząstek
MeV. O ile energia kinetyczna cząstek  musi przewyższać energię progową, aby powstające w wyniku reakcji protony miały zerową prędkość?
musi przewyższać energię progową, aby powstające w wyniku reakcji protony miały zerową prędkość?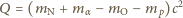
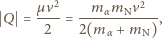
 jest prędkością progową cząstki
jest prędkością progową cząstki 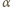 :
: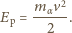
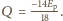 Oznaczmy przez
Oznaczmy przez 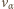 prędkość padającej cząstki
prędkość padającej cząstki 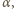 a przez
a przez 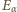 jej energię kinetyczną, gdy powstające protony mają zerową prędkość. Z zasady zachowania pędu:
jej energię kinetyczną, gdy powstające protony mają zerową prędkość. Z zasady zachowania pędu: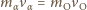
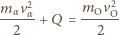
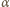 :
: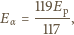
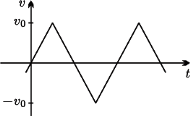
 do poziomu. Deska wykonuje podłużne oscylacje: jej prędkość zmienia się z dużą częstością w sposób przedstawiony na rysunku. Znaleźć średnią prędkość ciała, wiedząc, że amplituda zmian prędkości wynosi
do poziomu. Deska wykonuje podłużne oscylacje: jej prędkość zmienia się z dużą częstością w sposób przedstawiony na rysunku. Znaleźć średnią prędkość ciała, wiedząc, że amplituda zmian prędkości wynosi 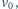 a współczynnik tarcia ciała o deskę jest równy
a współczynnik tarcia ciała o deskę jest równy 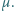
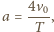 gdzie
gdzie 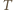 jest okresem drgań, a zwrot wektora przyspieszenia zmienia się co pół okresu. W układzie związanym z deską na ciało działa wzdłuż deski składowa siły ciężkości
jest okresem drgań, a zwrot wektora przyspieszenia zmienia się co pół okresu. W układzie związanym z deską na ciało działa wzdłuż deski składowa siły ciężkości 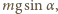 siła bezwładności
siła bezwładności 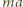 o zmiennym zwrocie oraz siła tarcia o wartości
o zmiennym zwrocie oraz siła tarcia o wartości 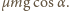 Ponieważ średnia prędkość ciała względem deski jest stała, musi ono przez pewną część okresu poruszać się w górę deski. Oznaczmy ten czas przez
Ponieważ średnia prędkość ciała względem deski jest stała, musi ono przez pewną część okresu poruszać się w górę deski. Oznaczmy ten czas przez 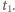 W czasie okresu pęd ciała nie ulega zmianie:
W czasie okresu pęd ciała nie ulega zmianie: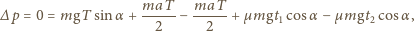
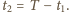 Stąd
Stąd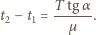
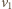 oznacza maksymalną prędkość klocka względem deski skierowaną w górę, a
oznacza maksymalną prędkość klocka względem deski skierowaną w górę, a 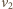 maksymalną prędkość skierowaną w dół.
maksymalną prędkość skierowaną w dół. 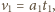 gdzie
gdzie 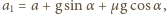
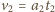 oraz
oraz 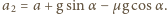 Ponieważ deska drga z dużą częstotliwością
Ponieważ deska drga z dużą częstotliwością 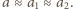 Ustalona średnia prędkość ciała
Ustalona średnia prędkość ciała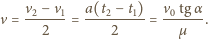
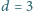 mm. Jakie powinno być ciśnienie zawartego w niej gazu, żeby jej
zapłon (zaświecenie) następował po przyłożeniu napięcia 100 V. Energia
jonizacji neonu wynosi
mm. Jakie powinno być ciśnienie zawartego w niej gazu, żeby jej
zapłon (zaświecenie) następował po przyłożeniu napięcia 100 V. Energia
jonizacji neonu wynosi
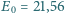 eV. Przyjmij, że temperatura gazu
w lampie wynosi
eV. Przyjmij, że temperatura gazu
w lampie wynosi
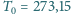 K. W warunkach normalnych droga
swobodna elektronu w neonie wynosi
K. W warunkach normalnych droga
swobodna elektronu w neonie wynosi
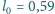
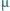 m.
m.
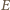 :
:
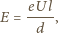
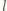 oznacza drogę swobodną elektronu (patrz zadanie 855),
oznacza drogę swobodną elektronu (patrz zadanie 855),
 ładunek elektronu, a
ładunek elektronu, a
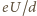 jest równe natężeniu pola
elektrycznego pomiędzy elektrodami. Oznacza to, że droga swobodna elektronu
powinna wynosić:
jest równe natężeniu pola
elektrycznego pomiędzy elektrodami. Oznacza to, że droga swobodna elektronu
powinna wynosić:
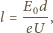
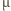 m. Droga swobodna jest odwrotnie proporcjonalna
do ciśnienia gazu, a więc w neonówce powinno panować ciśnienie
m. Droga swobodna jest odwrotnie proporcjonalna
do ciśnienia gazu, a więc w neonówce powinno panować ciśnienie
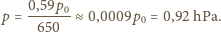
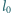 (tzw. średnią drogę swobodną)
przebywaną przez elektron pomiędzy dwoma zderzeniami z atomami
neonu znajdującego się w warunkach normalnych (tj. w temperaturze
(tzw. średnią drogę swobodną)
przebywaną przez elektron pomiędzy dwoma zderzeniami z atomami
neonu znajdującego się w warunkach normalnych (tj. w temperaturze
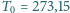 K i pod ciśnieniem
K i pod ciśnieniem
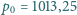 hPa). Promień
atomu neonu wynosi
hPa). Promień
atomu neonu wynosi
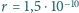 m.
m.
 od toru ruchu elektronu.
średnio nastąpi to, gdy w objętości
od toru ruchu elektronu.
średnio nastąpi to, gdy w objętości
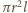 będzie znajdował się jeden
atom. Oznacza to warunek
będzie znajdował się jeden
atom. Oznacza to warunek
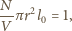
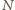 jest liczbą atomów, a
jest liczbą atomów, a
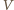 objętością naczynia. Dla gazu
w warunkach normalnych mamy
objętością naczynia. Dla gazu
w warunkach normalnych mamy
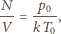
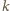 jest stałą Boltzmanna. Ostatecznie:
jest stałą Boltzmanna. Ostatecznie:
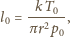
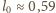
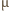 m.
m.