Klub 44F - zadania XII 2019»Zadanie 688
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania XII 2019
- Publikacja w Delcie: grudzień 2019
- Publikacja elektroniczna: 30 listopada 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (374 KB)

Na nieruchomej taśmie transportera leży klocek o masie 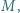 przyczepiony do ściany za pomocą sprężyny o współczynniku sprężystości
przyczepiony do ściany za pomocą sprężyny o współczynniku sprężystości 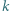 (rys. 1). Taśmę wprawiono w ruch ze stałą prędkością
(rys. 1). Taśmę wprawiono w ruch ze stałą prędkością 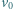 i po pewnym czasie ustaliły się drgania harmoniczne klocka. Znaleźć czas, po którym to nastąpiło, oraz amplitudę ustalonych drgań. Współczynnik tarcia klocka o taśmę jest równy
i po pewnym czasie ustaliły się drgania harmoniczne klocka. Znaleźć czas, po którym to nastąpiło, oraz amplitudę ustalonych drgań. Współczynnik tarcia klocka o taśmę jest równy 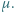

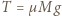 oraz siła sprężystości
oraz siła sprężystości 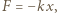 gdzie
gdzie 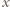 jest wydłużeniem sprężyny. Siły te równoważą się, gdy wydłużenie sprężyny osiąga wartość
jest wydłużeniem sprężyny. Siły te równoważą się, gdy wydłużenie sprężyny osiąga wartość 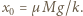 Musimy rozważyć dwa przypadki: 1) Klocek dojdzie do położenia równowagi z prędkością
Musimy rozważyć dwa przypadki: 1) Klocek dojdzie do położenia równowagi z prędkością 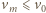 ; 2) Klocek osiągnie prędkość taśmy, zanim dojdzie do położenia równowagi.
; 2) Klocek osiągnie prędkość taśmy, zanim dojdzie do położenia równowagi.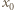 od położenia równowagi. Zależność wydłużenia sprężyny od czasu opisuje równanie
od położenia równowagi. Zależność wydłużenia sprężyny od czasu opisuje równanie 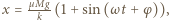 gdzie częstość drgań
gdzie częstość drgań 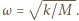 Przesunięcie fazowe
Przesunięcie fazowe 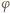 wyznaczamy z warunku początkowego
wyznaczamy z warunku początkowego 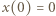 i otrzymujemy
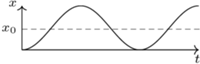
i otrzymujemy 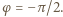 Zależność
Zależność 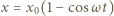 ilustruje rysunek 1. Prędkość klocka opisuje równanie
ilustruje rysunek 1. Prędkość klocka opisuje równanie 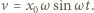 Prędkość maksymalna w położeniu równowagi wynosi
Prędkość maksymalna w położeniu równowagi wynosi 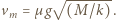
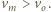 Klocek osiąga prędkość taśmy po czasie
Klocek osiąga prędkość taśmy po czasie 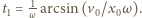 Tarcie staje się wtedy tarciem statycznym i równoważy siłę sprężystości. Klocek porusza się ruchem jednostajnym do chwili, gdy znajdzie się w położeniu równowagi, a tarcie ponownie osiągnie wartość
Tarcie staje się wtedy tarciem statycznym i równoważy siłę sprężystości. Klocek porusza się ruchem jednostajnym do chwili, gdy znajdzie się w położeniu równowagi, a tarcie ponownie osiągnie wartość 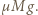 Od tego momentu tarcie pozostaje stałe, a klocek porusza się ruchem harmonicznym z taką samą częstością
Od tego momentu tarcie pozostaje stałe, a klocek porusza się ruchem harmonicznym z taką samą częstością 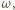 ale z inną amplitudą. Amplituda prędkości wynosi teraz
ale z inną amplitudą. Amplituda prędkości wynosi teraz 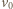 (z taką prędkością klocek przechodzi przez położenie równowagi), zatem amplituda drgań dana jest wzorem
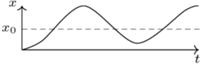
(z taką prędkością klocek przechodzi przez położenie równowagi), zatem amplituda drgań dana jest wzorem 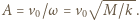 Ustalone drgania rozpoczną się po czasie
Ustalone drgania rozpoczną się po czasie 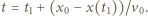 Ilustruje to rysunek 2.
Ilustruje to rysunek 2.