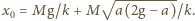Zadanie ZF-840
o zadaniu...
- Publikacja w Delcie: wrzesień 2013
- Publikacja elektroniczna: 31-08-2013
W środku sfery całkowicie pochłaniającej dochodzące do niej światło umieszczono lampę sodową. Lampa emituje światło z mocą 100 W. Przyjmując, że emitowane jest wyłącznie światło o długości fali 590 nm, obliczyć, ile fotonów w jednostce czasu pochłania sfera.
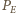 do energii
do energii
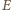 emitowanego
fotonu. Ponieważ
emitowanego
fotonu. Ponieważ
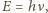 więc
więc
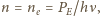 gdzie
gdzie
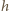 jest
stałą Plancka, a
jest
stałą Plancka, a
 częstością emitowanego światła. Podstawiając
częstością emitowanego światła. Podstawiając
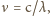 gdzie c jest prędkością światła, a
gdzie c jest prędkością światła, a
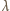 długością jego fali,
otrzymujemy ostatecznie
długością jego fali,
otrzymujemy ostatecznie
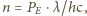 co dla wielkości danych
w zadaniu daje
co dla wielkości danych
w zadaniu daje
 fotonów na sekundę.
fotonów na sekundę.
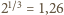 raza.
raza.
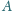 i
i
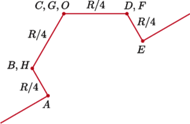
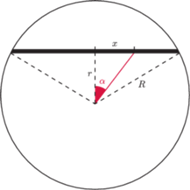
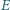 układu
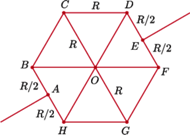
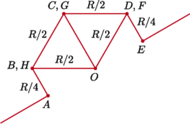
oporników w kształcie sześciokąta foremnego z przekątnymi (rysunek),
zbudowanego z 12 jednakowych elementów, o oporze
układu
oporników w kształcie sześciokąta foremnego z przekątnymi (rysunek),
zbudowanego z 12 jednakowych elementów, o oporze
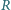 każdy.
każdy.
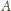 i
i
 Wynika stąd, że potencjał odpowiadających sobie punktów
leżących powyżej i poniżej tej prostej jest taki sam, tzn.
Wynika stąd, że potencjał odpowiadających sobie punktów
leżących powyżej i poniżej tej prostej jest taki sam, tzn.
 Łącząc punkty o jednakowym potencjale i zastępując
równocześnie opory, które zostaną przy tym połączone równolegle,
dostaniemy obwód zastępczy:
Łącząc punkty o jednakowym potencjale i zastępując
równocześnie opory, które zostaną przy tym połączone równolegle,
dostaniemy obwód zastępczy:
 moli gazu
moli gazu
 i
i
 moli gazu
moli gazu
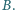 Molowe masy gazów oraz ich
molowe ciepła właściwe w stałej objętości i pod stałym ciśnieniem
wynoszą odpowiednio
Molowe masy gazów oraz ich
molowe ciepła właściwe w stałej objętości i pod stałym ciśnieniem
wynoszą odpowiednio
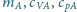 oraz
oraz
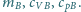 Ile
wynosi prędkość dźwięku
Ile
wynosi prędkość dźwięku
 w tej mieszaninie w temperaturze
w tej mieszaninie w temperaturze
 Uniwersalna stała gazowa wynosi
Uniwersalna stała gazowa wynosi
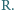
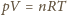 (
(
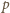 – ciśnienie,
– ciśnienie,
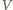 – objętość,
– objętość,
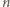 – całkowita liczba moli
gazu), dźwięk rozchodzi się z prędkością daną równaniem
– całkowita liczba moli
gazu), dźwięk rozchodzi się z prędkością daną równaniem
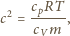
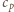 i
i
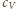 oznaczają ciepła molowe, odpowiednio w stałej
objętości i pod stałym ciśnieniem, a
oznaczają ciepła molowe, odpowiednio w stałej
objętości i pod stałym ciśnieniem, a
 masę jednego mola tego gazu.
Mieszanina gazów doskonałych spełnia równanie gazu doskonałego, masa i
ciepło są tzw. wielkościami ekstensywnymi, a więc odpowiednie wielkości dla
mieszaniny to
masę jednego mola tego gazu.
Mieszanina gazów doskonałych spełnia równanie gazu doskonałego, masa i
ciepło są tzw. wielkościami ekstensywnymi, a więc odpowiednie wielkości dla
mieszaniny to
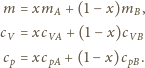
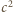 wynosi
wynosi
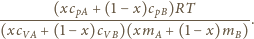
 w azocie).
w azocie).
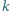 razy?
Zakładamy, że w obu przypadkach poziom wody nieznacznie przewyższa
tamę.
razy?
Zakładamy, że w obu przypadkach poziom wody nieznacznie przewyższa
tamę.
 przelewającej się wody zależy od wysokości
przelewającej się wody zależy od wysokości
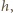 na jakiej
znajduje się jej powierzchnia nad poziomą krawędzią tamy, od przyspieszenia
ziemskiego
na jakiej
znajduje się jej powierzchnia nad poziomą krawędzią tamy, od przyspieszenia
ziemskiego
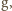 gęstości wody
gęstości wody
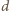 i jest proporcjonalna do długości
tamy
i jest proporcjonalna do długości
tamy
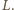 Mamy:
Mamy:
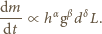
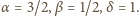 Ostatecznie ilość wody (jej masa)
przelewająca się w jednostce czasu wzrośnie
Ostatecznie ilość wody (jej masa)
przelewająca się w jednostce czasu wzrośnie
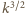 razy.
razy.
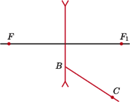
 wychodzącego
z soczewki rozpraszającej, której ogniska znajdują się w punktach
wychodzącego
z soczewki rozpraszającej, której ogniska znajdują się w punktach
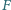 i
i
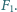 Znaleźć metodą geometryczną bieg promienia padającego na
soczewkę w punkcie
Znaleźć metodą geometryczną bieg promienia padającego na
soczewkę w punkcie
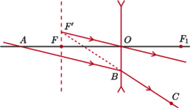
 (rysunek) pochodzi z wiązki
promieni równoległych padających na soczewkę.
(rysunek) pochodzi z wiązki
promieni równoległych padających na soczewkę.
 . W tym samym punkcie
. W tym samym punkcie
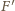 przetnie
więc płaszczyznę ogniskową, pochodzący z tej samej wiązki równoległej,
promień
przetnie
więc płaszczyznę ogniskową, pochodzący z tej samej wiązki równoległej,
promień
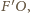 który nie zmienia swojego kierunku bo przechodzi przez
środek soczewki. Ponieważ promienie
który nie zmienia swojego kierunku bo przechodzi przez
środek soczewki. Ponieważ promienie
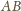 i
i
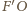 pochodzą z tej
samej wiązki równoległej, więc bieg promienia
pochodzą z tej
samej wiązki równoległej, więc bieg promienia
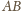 znajdujemy,
wykreślając prostą równoległą do
znajdujemy,
wykreślając prostą równoległą do
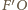 przechodzącą przez punkt
przechodzącą przez punkt
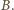
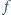 dźwięku piszczałki wypełnionej
helem, jeśli wypełniona powietrzem generuje dźwięk o częstotliwości
dźwięku piszczałki wypełnionej
helem, jeśli wypełniona powietrzem generuje dźwięk o częstotliwości
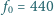 Hz? Prędkość
Hz? Prędkość
 dźwięku w gazie, w warunkach
normalnych, z dobrym przybliżeniem opisuje zależność
dźwięku w gazie, w warunkach
normalnych, z dobrym przybliżeniem opisuje zależność

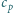 i
i
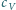 oznaczają odpowiednio ciepła właściwe gazu pod
stałym ciśnieniem i w stałej objętości,
oznaczają odpowiednio ciepła właściwe gazu pod
stałym ciśnieniem i w stałej objętości,
 –
temperaturę w skali Kelvina, a
–
temperaturę w skali Kelvina, a
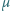 – masę jednego mola gazu. Powietrze jest
mieszaniną azotu (78% objętości) i tlenu (21% objętości).
– masę jednego mola gazu. Powietrze jest
mieszaniną azotu (78% objętości) i tlenu (21% objętości).
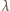 fali generowanego dźwięku jest proporcjonalna do
długości
fali generowanego dźwięku jest proporcjonalna do
długości
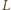 piszczałki (współczynnik zależy od rodzaju piszczałki i nie
zależy od rodzaju wypełniającego ją gazu), z definicji:
piszczałki (współczynnik zależy od rodzaju piszczałki i nie
zależy od rodzaju wypełniającego ją gazu), z definicji:
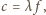 a więc
częstotliwość
a więc
częstotliwość
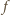 dźwięku danej piszczałki jest proporcjonalna do
prędkości dźwięku w wypełniającym ją gazie. Powietrze to w ponad
dźwięku danej piszczałki jest proporcjonalna do
prędkości dźwięku w wypełniającym ją gazie. Powietrze to w ponad
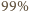 mieszanina dwuatomowych cząsteczek azotu
mieszanina dwuatomowych cząsteczek azotu
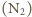 i tlenu
i tlenu
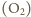 o wypadkowej masie molowej
o wypadkowej masie molowej
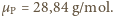 Cząsteczki
helu, gazu szlachetnego, są jednoatomowe:
Cząsteczki
helu, gazu szlachetnego, są jednoatomowe:
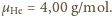 Jak
wiadomo, stosunek
Jak
wiadomo, stosunek
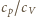 dla gazu jednoatomowego wynosi
w przybliżeniu 5/3, a dla gazu dwuatomowego 7/5. Po podstawieniu tych
danych otrzymujemy
dla gazu jednoatomowego wynosi
w przybliżeniu 5/3, a dla gazu dwuatomowego 7/5. Po podstawieniu tych
danych otrzymujemy
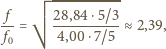
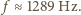

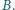 Napięcie między okładkami kondensatora wynosi
Napięcie między okładkami kondensatora wynosi
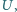 odległość między okładkami
odległość między okładkami
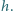 Z punktu
Z punktu
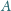 wylatuje
elektron prostopadle do linii pola magnetycznego. Jaki warunek musi spełniać
prędkość elektronu, żeby przeleciał on przez kondensator bez kontaktu z jego
okładkami? Siły ciężkości nie uwzględniamy, efekty relatywistyczne możemy
zaniedbać.
wylatuje
elektron prostopadle do linii pola magnetycznego. Jaki warunek musi spełniać
prędkość elektronu, żeby przeleciał on przez kondensator bez kontaktu z jego
okładkami? Siły ciężkości nie uwzględniamy, efekty relatywistyczne możemy
zaniedbać.
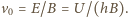 W układzie
W układzie
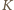 związanym z kondensatorem
elektron porusza się wtedy ruchem prostoliniowym z prędkością
związanym z kondensatorem
elektron porusza się wtedy ruchem prostoliniowym z prędkością
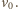 W układzie odniesienia
W układzie odniesienia
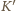 poruszającym się względem
poruszającym się względem
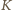 z prędkością
z prędkością
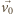 elektron ten spoczywa, czyli siła magnetyczna
na niego nie działa. Oznacza to, że w układzie
elektron ten spoczywa, czyli siła magnetyczna
na niego nie działa. Oznacza to, że w układzie
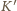 nie może również
działać siła elektryczna, czyli w układzie tym nie ma pola elektrycznego.
Elektron wylatujący z punktu
nie może również
działać siła elektryczna, czyli w układzie tym nie ma pola elektrycznego.
Elektron wylatujący z punktu
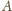 z prędkością
z prędkością
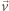 ma w układzie
ma w układzie
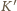 prędkość
prędkość
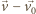 i porusza się po okręgu o promieniu
i porusza się po okręgu o promieniu
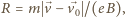 stycznym do prostej równoległej do prędkości
stycznym do prostej równoległej do prędkości
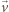 (
(
 i
i
 oznaczają odpowiednio masę i wartość
bezwzględną ładunku elektronu). Ponieważ mamy do czynienia z przypadkiem
nierelatywistycznym, wektor indukcji pola magnetycznego w układzie
oznaczają odpowiednio masę i wartość
bezwzględną ładunku elektronu). Ponieważ mamy do czynienia z przypadkiem
nierelatywistycznym, wektor indukcji pola magnetycznego w układzie
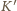 nadal wynosi
nadal wynosi
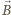 (patrz zadanie 560). W układzie związanym
z kondensatorem ruch elektronu jest złożeniem ruchu po okręgu oraz ruchu
postępowego z prędkością
(patrz zadanie 560). W układzie związanym
z kondensatorem ruch elektronu jest złożeniem ruchu po okręgu oraz ruchu
postępowego z prędkością
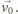 Elektron przeleci przez kondensator bez
kontaktu z okładkami, gdy
Elektron przeleci przez kondensator bez
kontaktu z okładkami, gdy
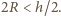 Zatem prędkość elektronu musi
spełniać warunki:
Zatem prędkość elektronu musi
spełniać warunki:
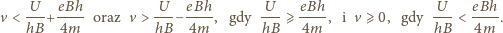
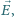 to w układzie poruszającym się z prędkością
to w układzie poruszającym się z prędkością
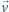 względem
układu pierwotnego, gdy możemy zaniedbać efekty relatywistyczne, istnieje
również pole magnetyczne
względem
układu pierwotnego, gdy możemy zaniedbać efekty relatywistyczne, istnieje
również pole magnetyczne
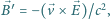 gdzie
gdzie
 jest
prędkością światła. Sprawdź prawdziwość tego stwierdzenia na przykładzie
pola od ładunku punktowego, rozważanego w obu układach.
jest
prędkością światła. Sprawdź prawdziwość tego stwierdzenia na przykładzie
pola od ładunku punktowego, rozważanego w obu układach.
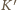 porusza się z prędkością
porusza się z prędkością
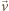 względem układu
inercjalnego
względem układu
inercjalnego
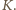 Rozważmy ładunek punktowy
Rozważmy ładunek punktowy
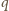 spoczywający
w początku układu
spoczywający
w początku układu
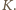 Pole elektryczne od tego ładunku w punkcie opisanym
wektorem położenia
Pole elektryczne od tego ładunku w punkcie opisanym
wektorem położenia
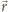 ma postać:
ma postać:
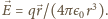 W układzie
W układzie
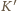 ładunek
ładunek
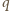 porusza się prędkością
porusza się prędkością
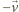 i w przybliżeniu
nierelatywistycznym możemy go potraktować jako stały prąd elektryczny.
Natężenie prądu dane jest wzorem
i w przybliżeniu
nierelatywistycznym możemy go potraktować jako stały prąd elektryczny.
Natężenie prądu dane jest wzorem
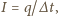 gdzie
gdzie
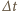 jest
czasem, w którym ładunek przemieszcza się o
jest
czasem, w którym ładunek przemieszcza się o
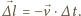 Stąd
Stąd
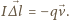 Zgodnie z prawem Biota–Savarta pole magnetyczne
wytworzone w układzie
Zgodnie z prawem Biota–Savarta pole magnetyczne
wytworzone w układzie
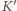 przez poruszający się ładunek ma
postać:
przez poruszający się ładunek ma
postać:
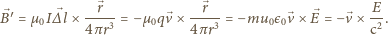
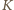 obok pola elektrycznego występuje
również pole magnetyczne
obok pola elektrycznego występuje
również pole magnetyczne
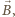 pole magnetyczne w układzie
pole magnetyczne w układzie
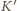 ma postać:
ma postać:
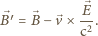
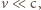 kiedy możemy
zaniedbać opóźnienie związane ze skończonym rozchodzeniem się sygnału
elektromagnetycznego. Otrzymany wzór pokazuje, że w przybliżeniu
nierelatywistycznym pole magnetyczne nie zmienia się przy przejściu z jednego
układu inercjalnego do innego.
kiedy możemy
zaniedbać opóźnienie związane ze skończonym rozchodzeniem się sygnału
elektromagnetycznego. Otrzymany wzór pokazuje, że w przybliżeniu
nierelatywistycznym pole magnetyczne nie zmienia się przy przejściu z jednego
układu inercjalnego do innego.

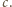 Dla wody
Dla wody
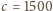 m/s.
Zmiana prędkości wody wywołana zamknięciem zaworu w czasie
m/s.
Zmiana prędkości wody wywołana zamknięciem zaworu w czasie
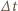 dotrze na odległość
dotrze na odległość
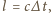 zatrzymana zostanie
masa wody
zatrzymana zostanie
masa wody
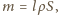 gdzie
gdzie
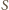 jest polem przekroju rury,
a
jest polem przekroju rury,
a
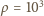 kg/m
kg/m
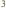 oznacza gęstość wody. Zmiana pędu
wody wynosi
oznacza gęstość wody. Zmiana pędu
wody wynosi
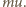 Ciśnienie
Ciśnienie
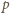 wody na zawór wyniesie
więc
wody na zawór wyniesie
więc
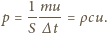
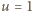 m/s ciśnienie jest równe
m/s ciśnienie jest równe
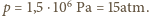
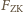 ) niż przez Słońce (siłą
) niż przez Słońce (siłą
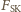 ) w punktach, dla których
Księżyc znajduje się między Ziemią a Słońcem. Tymczasem w punktach,
w których Księżyc znajduje się najbliżej Słońca, stosunek tych sił
przyciągania wynosi
) w punktach, dla których
Księżyc znajduje się między Ziemią a Słońcem. Tymczasem w punktach,
w których Księżyc znajduje się najbliżej Słońca, stosunek tych sił
przyciągania wynosi
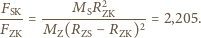
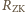 w mianowniku jest zaniedbywalny w porównaniu
z
w mianowniku jest zaniedbywalny w porównaniu
z
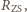 toteż wypadkowa sił działających na Księżyc jest stale
skierowana w stronę Słońca. Oznacza to, że Księżyc stale skręca w stronę
Słońca i rozważany w zadaniu „trójkąt” jest zawsze wypukły.
toteż wypadkowa sił działających na Księżyc jest stale
skierowana w stronę Słońca. Oznacza to, że Księżyc stale skręca w stronę
Słońca i rozważany w zadaniu „trójkąt” jest zawsze wypukły.

 Jaką wartość musi mieć kąt
Jaką wartość musi mieć kąt
 między podstawą
a ścianką naczynia, aby przez boczną ściankę nie było widać monety
umieszczonej pod dnem naczynia?
między podstawą
a ścianką naczynia, aby przez boczną ściankę nie było widać monety
umieszczonej pod dnem naczynia?

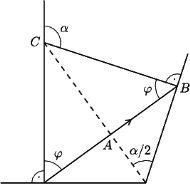
 będzie kątem załamania promienia przechodzącego z warstwy
powietrza między monetą a dnem naczynia do wody (
będzie kątem załamania promienia przechodzącego z warstwy
powietrza między monetą a dnem naczynia do wody ( nie przekracza wartości kąta granicznego
nie przekracza wartości kąta granicznego
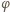 :
:
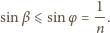
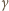 nie wyjdzie
na zewnątrz, gdy
nie wyjdzie
na zewnątrz, gdy
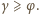 Zmniejszenie kąta
Zmniejszenie kąta
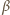 powoduje
zwiększenie kąta
powoduje
zwiększenie kąta
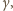 wystarczy więc rozważyć przypadek graniczny, gdy
wystarczy więc rozważyć przypadek graniczny, gdy
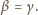 Rozważmy sytuację, gdy oba kąty
Rozważmy sytuację, gdy oba kąty
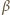 i
i
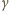 mają
wartość graniczną. W trójkącie
mają
wartość graniczną. W trójkącie
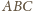 na
na 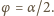 Zatem nie zobaczymy monety przez boczną ściankę, gdy
Zatem nie zobaczymy monety przez boczną ściankę, gdy
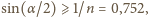 czyli
czyli
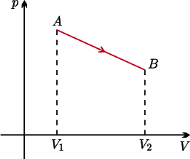
 Końce odcinka
Końce odcinka
 leżą na tej samej izotermie,
a odpowiadające im objętości wynoszą
leżą na tej samej izotermie,
a odpowiadające im objętości wynoszą
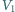 i
i
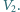 Jaka jest część
odcinka
Jaka jest część
odcinka
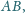 dla której gaz pobiera ciepło w tej przemianie?
dla której gaz pobiera ciepło w tej przemianie?
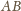 zmienia się liniowo zgodnie ze wzorem
zmienia się liniowo zgodnie ze wzorem
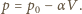 Oznaczając przez
Oznaczając przez
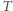 temperaturę w punktach
temperaturę w punktach
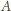 i
i
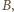 otrzymujemy, korzystając z równania Clapeyrona
otrzymujemy, korzystając z równania Clapeyrona
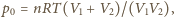
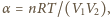 gdzie
gdzie
 oznacza
liczbę moli gazu, a
oznacza
liczbę moli gazu, a
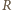 jest stałą gazową. Rozważmy badaną przemianę
w małym przedziale objętości
jest stałą gazową. Rozważmy badaną przemianę
w małym przedziale objętości
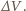 Zgodnie z pierwszą zasadą
termodynamiki ciepło tam przekazane wynosi
Zgodnie z pierwszą zasadą
termodynamiki ciepło tam przekazane wynosi
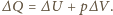 Zmiana
energii wewnętrznej dana jest wzorem
Zmiana
energii wewnętrznej dana jest wzorem
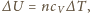 gdzie molowe ciepło
właściwe
gdzie molowe ciepło
właściwe
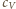 przy stałej objętości dla gazu jednoatomowego
wynosi
przy stałej objętości dla gazu jednoatomowego
wynosi
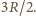 Zmiana temperatury w badanym przedziale wynosi
Zmiana temperatury w badanym przedziale wynosi
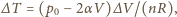 gdzie pominęliśmy wyraz proporcjonalny do
gdzie pominęliśmy wyraz proporcjonalny do
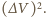 Gaz pobiera ciepło, gdy
Gaz pobiera ciepło, gdy
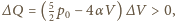 czyli
gdy
czyli
gdy
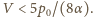 Zatem ciepło w przemianie
Zatem ciepło w przemianie
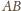 pobierane
jest na odcinku
pobierane
jest na odcinku
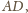 gdzie objętość, odpowiadająca punktowi
gdzie objętość, odpowiadająca punktowi
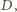 wynosi
wynosi
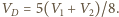

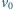 dziewczęcia w momencie
złapania. Po skończonym czasie dziewczę, przez cały czas kurczowo trzymające
się liny, zderza się ze słupem. Jaka jest prędkość dziewczęcia w chwili
zderzenia?
dziewczęcia w momencie
złapania. Po skończonym czasie dziewczę, przez cały czas kurczowo trzymające
się liny, zderza się ze słupem. Jaka jest prędkość dziewczęcia w chwili
zderzenia?

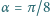 do poziomu. Jaki ułamek całkowitej długości liny może
stanowić część wisząca w powietrzu?
do poziomu. Jaki ułamek całkowitej długości liny może
stanowić część wisząca w powietrzu?
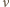 stosunek długości wiszącej części liny do całkowitej
długości liny. Niech
stosunek długości wiszącej części liny do całkowitej
długości liny. Niech
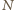 będzie naprężeniem liny tam, gdzie zaczyna
się jej wisząca część. Warunek równowagi dla wiszącej części to
będzie naprężeniem liny tam, gdzie zaczyna
się jej wisząca część. Warunek równowagi dla wiszącej części to
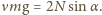 Z kolei siła tarcia statycznego jednej z dwóch leżących
części liny
Z kolei siła tarcia statycznego jednej z dwóch leżących
części liny
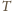 nie może przekraczać nacisku tej części liny na
zbocze; nacisk ten jest równy
nie może przekraczać nacisku tej części liny na
zbocze; nacisk ten jest równy
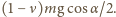 Ta siła tarcia
musi zrównoważyć dwie siły: składową siły grawitacji wzdłuż zbocza
Ta siła tarcia
musi zrównoważyć dwie siły: składową siły grawitacji wzdłuż zbocza
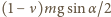 działającą na leżącą część liny oraz naprężenie liny
działającą na leżącą część liny oraz naprężenie liny
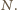 Podstawiając wartości funkcji trygonometrycznych, otrzymujemy
maksymalną wartość
Podstawiając wartości funkcji trygonometrycznych, otrzymujemy
maksymalną wartość
 równą
równą
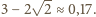 Co ciekawe, jest
to maksymalna część długości liny, jaka może wisieć w powietrzu dla
dowolnego kąta
Co ciekawe, jest
to maksymalna część długości liny, jaka może wisieć w powietrzu dla
dowolnego kąta

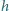 nad poziomem wody. Rejestruje on sygnały wysyłane przez satelitę
wznoszącego się nad horyzontem. Przy jakich kątach wzniesienia satelity nad
horyzontem obserwuje się maksima sygnału? Długość fali emitowanej przez
satelitę wynosi
nad poziomem wody. Rejestruje on sygnały wysyłane przez satelitę
wznoszącego się nad horyzontem. Przy jakich kątach wzniesienia satelity nad
horyzontem obserwuje się maksima sygnału? Długość fali emitowanej przez
satelitę wynosi
 Przyjmujemy, że powierzchnia jeziora jest idealnie
gładka.
Przyjmujemy, że powierzchnia jeziora jest idealnie
gładka.
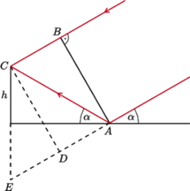
 możemy przyjąć, że wiązka promieniowania wysyłanego przez
satelitę jest równoległa. Do odbiornika w punkcie
możemy przyjąć, że wiązka promieniowania wysyłanego przez
satelitę jest równoległa. Do odbiornika w punkcie
 docierają
promienie biegnące bezpośrednio od satelity i odbite od powierzchni
jeziora, jak na rysunku. Punkty
docierają
promienie biegnące bezpośrednio od satelity i odbite od powierzchni
jeziora, jak na rysunku. Punkty
 i
i
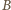 leżą na tej samej
powierzchni falowej i mają zgodną fazę. Ich różnica dróg jest równa
leżą na tej samej
powierzchni falowej i mają zgodną fazę. Ich różnica dróg jest równa
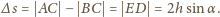 Jeden z promieni odbija się od
ośrodka, w którym prędkość rozchodzenia się fali jest mniejsza niż
w powietrzu. Powoduje to zmianę fazy o
Jeden z promieni odbija się od
ośrodka, w którym prędkość rozchodzenia się fali jest mniejsza niż
w powietrzu. Powoduje to zmianę fazy o
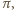 odpowiadającą przebytej
drodze
odpowiadającą przebytej
drodze
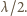 Uwzględniając to, otrzymujemy wzór na maksima
interferencyjne:
Uwzględniając to, otrzymujemy wzór na maksima
interferencyjne:
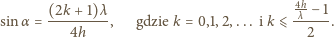
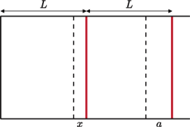
 i
i
 na prawo od
zamkniętego końca znajdują się dwa tłoki, które mogą przemieszczać się bez
tarcia (grubości tłoków pomijamy). W lewej części znajduje się para
wodna pod ciśnieniem
na prawo od
zamkniętego końca znajdują się dwa tłoki, które mogą przemieszczać się bez
tarcia (grubości tłoków pomijamy). W lewej części znajduje się para
wodna pod ciśnieniem
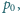 w prawej powietrze o takim samym
ciśnieniu. Ciśnienie pary nasyconej wody w danej temperaturze wynosi
w prawej powietrze o takim samym
ciśnieniu. Ciśnienie pary nasyconej wody w danej temperaturze wynosi
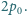 Prawy tłok został wolno wepchnięty na odległość
Prawy tłok został wolno wepchnięty na odległość
 O ile
przesunął się lewy tłok? Temperatura jest stała.
O ile
przesunął się lewy tłok? Temperatura jest stała.
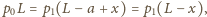 gdzie
gdzie
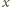 jest
przesunięciem tłoka lewego, zatem
jest
przesunięciem tłoka lewego, zatem
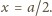 Ciśnienie
Ciśnienie
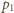 nie
przekracza ciśnienia pary nasyconej:
nie
przekracza ciśnienia pary nasyconej:
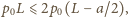 stąd
stąd
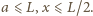
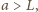 para wodna w lewej komorze zaczyna się skraplać,
ciśnienie ma stałą wartość
para wodna w lewej komorze zaczyna się skraplać,
ciśnienie ma stałą wartość
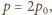 a objętości gazów w obu
częściach są takie same (zaniedbujemy objętość wody powstałej w wyniku
skroplenia w porównaniu z objętością pary nasyconej o tej samej masie).
Oznaczając dodatkowe przesunięcia obu tłoków przez
a objętości gazów w obu
częściach są takie same (zaniedbujemy objętość wody powstałej w wyniku
skroplenia w porównaniu z objętością pary nasyconej o tej samej masie).
Oznaczając dodatkowe przesunięcia obu tłoków przez
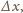 możemy
napisać:
możemy
napisać:
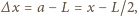 stąd
stąd
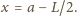 Ostatecznie:
Ostatecznie:
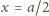 dla
dla
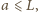
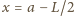 dla
dla
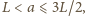
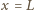 dla
dla
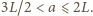
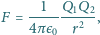 jak
w układzie SI, tylko jako
jak
w układzie SI, tylko jako

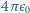 na
jedynkę. Jak dokonać transformacji odwrotnej? Ile wynosi ładunek elementarny
w tych układach?
na
jedynkę. Jak dokonać transformacji odwrotnej? Ile wynosi ładunek elementarny
w tych układach?
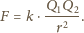
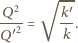
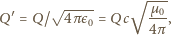
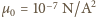 jest przenikalnością magnetyczną próżni.
Podstawiając wartości liczbowe dla ładunku elementarnego, otrzymujemy
jest przenikalnością magnetyczną próżni.
Podstawiając wartości liczbowe dla ładunku elementarnego, otrzymujemy
 lewituje w nieskończonym
niebieskim pastwisku o temperaturze
lewituje w nieskończonym
niebieskim pastwisku o temperaturze
 Krowy są dobrymi przewodnikami
elektryczności. Oszacować wielkość ładunku zgromadzonego na
krowie.
Krowy są dobrymi przewodnikami
elektryczności. Oszacować wielkość ładunku zgromadzonego na
krowie.
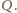 Wytwarza on
pole elektryczne o natężeniu
Wytwarza on
pole elektryczne o natężeniu
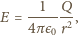
 jest odległością od środka krowy. Gęstość energii pola
elektrycznego wyraża się wzorem
jest odległością od środka krowy. Gęstość energii pola
elektrycznego wyraża się wzorem
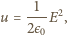
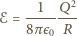
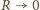 otrzymujemy znany problem nieskończonej energii ładunku
punktowego). Skoro krowa jest elementarna, to z zasady ekwipartycji energii
„należy się” jej
otrzymujemy znany problem nieskończonej energii ładunku
punktowego). Skoro krowa jest elementarna, to z zasady ekwipartycji energii
„należy się” jej
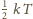 na każdy stopień swobody. Dla ruchu
dwuwymiarowego otrzymujemy więc
na każdy stopień swobody. Dla ruchu
dwuwymiarowego otrzymujemy więc
 co dla
co dla
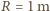 i
i
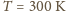 daje
daje
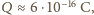 czyli kilka tysięcy
ładunków elementarnych.
czyli kilka tysięcy
ładunków elementarnych.
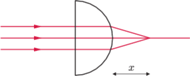
 skupia się w odległości
skupia się w odległości
 od powierzchni wypukłej.
W jakiej odległości od powierzchni płaskiej skupią się promienie, jeżeli wiązkę
światła przepuścimy przez półkulę z drugiej strony?
od powierzchni wypukłej.
W jakiej odległości od powierzchni płaskiej skupią się promienie, jeżeli wiązkę
światła przepuścimy przez półkulę z drugiej strony?
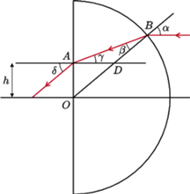
 Gdy wiązka pada
prostopadle na płaską powierzchnię szkła, biegnie przez szkło bez zmiany
kierunku. Odległość
Gdy wiązka pada
prostopadle na płaską powierzchnię szkła, biegnie przez szkło bez zmiany
kierunku. Odległość
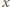 nie zmieni się, gdy wiązkę przepuścimy przez
cienką soczewkę płasko-wypukłą ze szkła o promieniu krzywizny
nie zmieni się, gdy wiązkę przepuścimy przez
cienką soczewkę płasko-wypukłą ze szkła o promieniu krzywizny
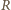 umieszczoną w powietrzu (
umieszczoną w powietrzu (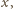 mamy więc związek
mamy więc związek
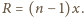
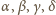 kąty padania i załamania przy przechodzeniu światła
z jednego ośrodka do drugiego, jak na
kąty padania i załamania przy przechodzeniu światła
z jednego ośrodka do drugiego, jak na 
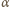 jest kątem zewnętrznym w trójkącie
jest kątem zewnętrznym w trójkącie
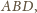 zatem
zatem
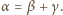 Niech
Niech
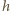 będzie odległością promienia wychodzącego
z półkuli od osi optycznej. Stosując twierdzenie sinusów do trójkąta
będzie odległością promienia wychodzącego
z półkuli od osi optycznej. Stosując twierdzenie sinusów do trójkąta
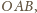 otrzymujemy:
otrzymujemy:
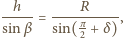 a w przybliżeniu
a w przybliżeniu
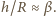 Szukaną odległość
Szukaną odległość
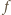 punktu skupienia promieni od
powierzchni płaskiej dostajemy ze związków:
punktu skupienia promieni od
powierzchni płaskiej dostajemy ze związków:
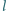 i współczynniku sprężystości
i współczynniku sprężystości
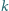 zsuwa się w kierunku pionowym żelazny pierścień o masie
zsuwa się w kierunku pionowym żelazny pierścień o masie
 Siła tarcia między powierzchnią sznura a pierścieniem wynosi
Siła tarcia między powierzchnią sznura a pierścieniem wynosi
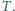 Wyznacz ciepło, które się przy tym wydziela.
Wyznacz ciepło, które się przy tym wydziela.
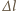 maksymalne wydłużenie sznura. Stwierdzenie, że
pierścień jest żelazny, wskazuje, że masę sznura możemy zaniedbać
w porównaniu z masą pierścienia. Wtedy mamy
maksymalne wydłużenie sznura. Stwierdzenie, że
pierścień jest żelazny, wskazuje, że masę sznura możemy zaniedbać
w porównaniu z masą pierścienia. Wtedy mamy
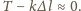 Na
sznur działa siła tarcia, która powoduje jego wydłużenie, czyli
wzrost energii sprężystości oraz wydzielanie się ciepła
Na
sznur działa siła tarcia, która powoduje jego wydłużenie, czyli
wzrost energii sprężystości oraz wydzielanie się ciepła
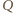 :
:
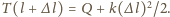 Wiedząc, że
Wiedząc, że
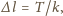 otrzymujemy:
otrzymujemy:
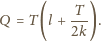
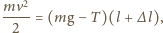 natomiast zasada
zachowania energii dla całego układu sznur–pierścień ma postać:
natomiast zasada
zachowania energii dla całego układu sznur–pierścień ma postać:
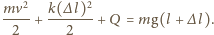 Odejmując te równania stronami,
otrzymujemy taki sam wynik jak poprzednio.
Odejmując te równania stronami,
otrzymujemy taki sam wynik jak poprzednio.
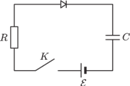
 w obwodzie przedstawionym na
rysunku (a) po zamknięciu klucza? W chwili początkowej kondensator
o pojemności
w obwodzie przedstawionym na
rysunku (a) po zamknięciu klucza? W chwili początkowej kondensator
o pojemności
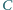 nie jest naładowany. Siła elektromotoryczna źródła
prądu wynosi
nie jest naładowany. Siła elektromotoryczna źródła
prądu wynosi
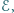 opór wewnętrzny źródła jest zaniedbywalny.
Wyidealizowana charakterystyka prądowo-napięciowa diody przedstawiona jest
na rysunku (b).
opór wewnętrzny źródła jest zaniedbywalny.
Wyidealizowana charakterystyka prądowo-napięciowa diody przedstawiona jest
na rysunku (b).
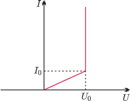
 czyli spełniony jest warunek
czyli spełniony jest warunek
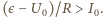 Podczas
ładowania kondensatora natężenie prądu maleje i w pewnym czasie
Podczas
ładowania kondensatora natężenie prądu maleje i w pewnym czasie
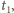 dopóki nie osiągnie wartości
dopóki nie osiągnie wartości
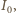 napięcie na diodzie ma
stałą wartość
napięcie na diodzie ma
stałą wartość
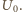 Ładunek, którym naładuje się w tym czasie
kondensator, wynosi
Ładunek, którym naładuje się w tym czasie
kondensator, wynosi
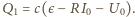 Zgodnie z zasadą zachowania
energii:
Zgodnie z zasadą zachowania
energii:
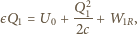
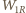 jest ciepłem wydzielonym na oporze
jest ciepłem wydzielonym na oporze
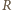 w czasie
w czasie
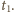 W czasie
W czasie
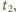 gdy natężenie prądu w obwodzie jest
mniejsze niż
gdy natężenie prądu w obwodzie jest
mniejsze niż
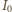 i maleje do zera, napięcie na diodzie maleje liniowo
z natężeniem prądu, czyli jej opór
i maleje do zera, napięcie na diodzie maleje liniowo
z natężeniem prądu, czyli jej opór
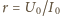 jest stały. Ładunek, który
przepływa w tym czasie w obwodzie, wynosi
jest stały. Ładunek, który
przepływa w tym czasie w obwodzie, wynosi
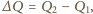 gdzie
końcowy ładunek na kondensatorze to
gdzie
końcowy ładunek na kondensatorze to
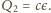 Energia wydzielona
w tym czasie w obwodzie równa jest pracy źródła i wynosi
Energia wydzielona
w tym czasie w obwodzie równa jest pracy źródła i wynosi
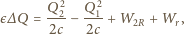
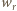 jest ciepłem wydzielonym na diodzie, a
jest ciepłem wydzielonym na diodzie, a
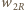 ciepłem
wydzielonym na oporze
ciepłem
wydzielonym na oporze
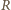 w czasie
w czasie
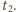 Ponieważ dioda i opornik
są połączone szeregowo i w każdej chwili płynie przez nie prąd o tym samym
natężeniu, zachodzi związek
Ponieważ dioda i opornik
są połączone szeregowo i w każdej chwili płynie przez nie prąd o tym samym
natężeniu, zachodzi związek
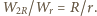 Całkowite ciepło wydzielone
na oporze
Całkowite ciepło wydzielone
na oporze
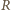 w czasie
w czasie
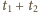 wynosi
wynosi
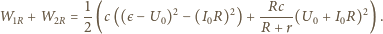
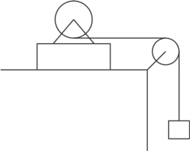
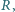 który może swobodnie obracać się wokół własnej osi. Do końca
nici nawiniętej na walec i przerzuconej przez nieruchomy bloczek, jak na
rysunku, przymocowano ciężarek. Masy podstawki, walca i ciężarka są
jednakowe. Ile obrotów wykona walec w czasie
który może swobodnie obracać się wokół własnej osi. Do końca
nici nawiniętej na walec i przerzuconej przez nieruchomy bloczek, jak na
rysunku, przymocowano ciężarek. Masy podstawki, walca i ciężarka są
jednakowe. Ile obrotów wykona walec w czasie
 W chwili początkowej
układ spoczywa. Tarcie można zaniedbać.
W chwili początkowej
układ spoczywa. Tarcie można zaniedbać.
 Równanie
ruchu ciężarka ma postać
Równanie
ruchu ciężarka ma postać
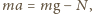 gdzie
gdzie
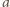 jest jego
przyspieszeniem, a
jest jego
przyspieszeniem, a
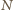 siłą naprężenia nici.
siłą naprężenia nici.
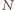 jest jedyną siłą
działającą w kierunku poziomym na układ podstawki i walca, zatem
oznaczając przez
jest jedyną siłą
działającą w kierunku poziomym na układ podstawki i walca, zatem
oznaczając przez
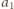 przyspieszenie ruchu postępowego tego układu,
możemy napisać:
przyspieszenie ruchu postępowego tego układu,
możemy napisać:
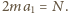 Moment bezwładności pełnego
walca względem jego osi wynosi
Moment bezwładności pełnego
walca względem jego osi wynosi
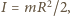 a równanie ruchu
obrotowego względem tej osi ma postać
a równanie ruchu
obrotowego względem tej osi ma postać
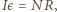 gdzie
gdzie
 jest
przyspieszeniem kątowym. Przyspieszenie względem Ziemi najniżej
położonego punktu walca równe jest przyspieszeniu ciężarka, mamy więc
związek
jest
przyspieszeniem kątowym. Przyspieszenie względem Ziemi najniżej
położonego punktu walca równe jest przyspieszeniu ciężarka, mamy więc
związek
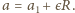 Eliminując z wypisanych równań przyspieszenia
liniowe oraz naprężenie nici, otrzymujemy wzór na przyspieszenie kątowe
walca:
Eliminując z wypisanych równań przyspieszenia
liniowe oraz naprężenie nici, otrzymujemy wzór na przyspieszenie kątowe
walca:
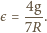
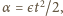 zatem szukana liczba obrotów
to
zatem szukana liczba obrotów
to
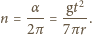
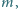 a jej prędkość tuż przed odbiciem wynosiła
a jej prędkość tuż przed odbiciem wynosiła
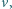 to
zmiana pędu piłeczki przy odbiciu jest równa
to
zmiana pędu piłeczki przy odbiciu jest równa
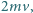 energia zaś się
nie zmienia. Jak to możliwe, że zachodzi przekaz pędu bez przekazu
energii?
energia zaś się
nie zmienia. Jak to możliwe, że zachodzi przekaz pędu bez przekazu
energii?
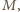 to zasadę zachowania pędu i energii dla ruchu jednowymiarowego
przy założeniu, że ciężkie ciało początkowo spoczywa, możemy zapisać
jako:
to zasadę zachowania pędu i energii dla ruchu jednowymiarowego
przy założeniu, że ciężkie ciało początkowo spoczywa, możemy zapisać
jako:
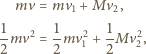
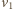 i
i
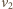 są odpowiednio prędkościami piłeczki
i ciężkiego ciała tuż po odbiciu. Są one równe
są odpowiednio prędkościami piłeczki
i ciężkiego ciała tuż po odbiciu. Są one równe
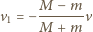
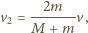
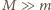 rzeczywiście mamy
rzeczywiście mamy
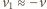 oraz
oraz
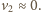
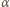 przyjmuje wartości bardzo
bliskie zeru. Uzasadnia to przybliżenie
przyjmuje wartości bardzo
bliskie zeru. Uzasadnia to przybliżenie
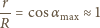
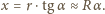
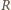 i ich przyspieszenia kątowego
i ich przyspieszenia kątowego
 względem środka Ziemi.
Składowa siły grawitacji wzdłuż tunelu
względem środka Ziemi.
Składowa siły grawitacji wzdłuż tunelu
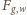 wyraża się wzorem
wyraża się wzorem
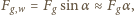 gdzie
gdzie
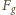 jest całkowitą siłą grawitacji
działającą na wagon. Dla wagonu o masie
jest całkowitą siłą grawitacji
działającą na wagon. Dla wagonu o masie
 mamy więc
mamy więc
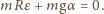
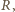 wagonik będzie więc wykonywał ruch okresowy o okresie
wagonik będzie więc wykonywał ruch okresowy o okresie
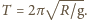 Podróż z Delty do Albionu zajmuje pół okresu, zatem
szukany czas jest równy
Podróż z Delty do Albionu zajmuje pół okresu, zatem
szukany czas jest równy
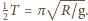 Podstawiając wartości liczbowe,
uzyskujemy czas przejazdu równy 42 minuty, niezależny od odległości
między Deltą i Albionem.
Podstawiając wartości liczbowe,
uzyskujemy czas przejazdu równy 42 minuty, niezależny od odległości
między Deltą i Albionem.
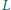 dołączono do górnych końców dwóch
równoległych szyn przewodzących ustawionych pionowo. Odstęp między
szynami jest równy
dołączono do górnych końców dwóch
równoległych szyn przewodzących ustawionych pionowo. Odstęp między
szynami jest równy
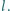 Jednorodne pole magnetyczne o indukcji
Jednorodne pole magnetyczne o indukcji
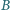 ma kierunek poziomy i jest prostopadłe do płaszczyzny szyn. Poziomy,
przewodzący pręt o masie
ma kierunek poziomy i jest prostopadłe do płaszczyzny szyn. Poziomy,
przewodzący pręt o masie
 może poruszać się w polu magnetycznym
wzdłuż szyn w ten sposób, że stale się z nimi styka. Opór i samoindukcję
przewodników oraz tarcie pręta o szyny zaniedbujemy. Znaleźć zależność
położenia pręta od czasu
może poruszać się w polu magnetycznym
wzdłuż szyn w ten sposób, że stale się z nimi styka. Opór i samoindukcję
przewodników oraz tarcie pręta o szyny zaniedbujemy. Znaleźć zależność
położenia pręta od czasu
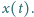 Prędkość początkowa pręta jest równa
zeru.
Prędkość początkowa pręta jest równa
zeru.
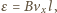 gdzie
gdzie
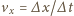 jest szybkością zmian położenia pręta. Prąd indukcyjny
płynie w takim kierunku, żeby przeciwdziałać zmianom strumienia pola
magnetycznego, które go wywołują, czyli siła elektrodynamiczna działająca na
pręt ma zwrot przeciwny do siły ciężkości. Równanie ruchu pręta ma
więc postać
jest szybkością zmian położenia pręta. Prąd indukcyjny
płynie w takim kierunku, żeby przeciwdziałać zmianom strumienia pola
magnetycznego, które go wywołują, czyli siła elektrodynamiczna działająca na
pręt ma zwrot przeciwny do siły ciężkości. Równanie ruchu pręta ma
więc postać
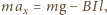 gdzie
gdzie
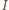 jest natężeniem
prądu w obwodzie. Możemy też napisać drugie prawo Kirchhoffa dla
obwodu zawierającego pręt i cewkę:
jest natężeniem
prądu w obwodzie. Możemy też napisać drugie prawo Kirchhoffa dla
obwodu zawierającego pręt i cewkę:
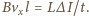 Uwzględniając
warunki początkowe
Uwzględniając
warunki początkowe
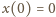 oraz
oraz
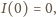 otrzymujemy
otrzymujemy
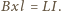 Wstawiając otrzymane stąd wyrażenie na natężenie prądu do
równania ruchu, możemy zapisać je w postaci
Wstawiając otrzymane stąd wyrażenie na natężenie prądu do
równania ruchu, możemy zapisać je w postaci
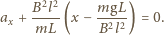
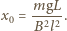
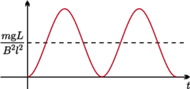
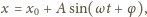 gdzie częstość drgań jest równa
gdzie częstość drgań jest równa
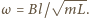 Zależność prędkości od czasu ma postać
Zależność prędkości od czasu ma postać
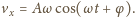 Amplitudę drgań
Amplitudę drgań
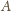 i fazę
początkową
i fazę
początkową
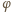 możemy wyznaczyć z warunków początkowych:
możemy wyznaczyć z warunków początkowych:
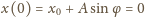 oraz
oraz
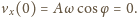 Uwzględniając,
że
Uwzględniając,
że
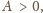 otrzymujemy
otrzymujemy
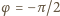 oraz
oraz
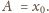 Ostatecznie
zależność położenia pręta od czasu ma postać
Ostatecznie
zależność położenia pręta od czasu ma postać
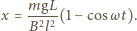

 Górny koniec pręta jest zamocowany przegubowo. Kąt między
prętem i kartką wynosi
Górny koniec pręta jest zamocowany przegubowo. Kąt między
prętem i kartką wynosi
 współczynnik tarcia między nimi wynosi
współczynnik tarcia między nimi wynosi
 Między kartką a stołem tarcia nie ma. Jaką minimalną, poziomą siłę
trzeba przyłożyć do kartki, aby wyciągnąć ją spod pręta?
Między kartką a stołem tarcia nie ma. Jaką minimalną, poziomą siłę
trzeba przyłożyć do kartki, aby wyciągnąć ją spod pręta?
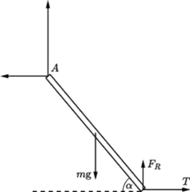
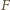 przekroczy
maksymalną wartość tarcia statycznego między prętem i kartką:
przekroczy
maksymalną wartość tarcia statycznego między prętem i kartką:
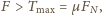 gdzie
gdzie
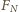 jest siłą nacisku pręta na kartkę, równą
co do wartości sile reakcji
jest siłą nacisku pręta na kartkę, równą
co do wartości sile reakcji
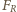 kartki na pręt. Rozważmy sytuację
graniczną, gdy siła tarcia osiągnęła maksymalną wartość, a układ pozostaje
jeszcze w równowadze. Oznacza to, że wszystkie siły działające na pręt
równoważą się, a wypadkowy moment tych sił względem dowolnego punktu
wynosi 0. Warunek równowagi momentów sił względem punktu
kartki na pręt. Rozważmy sytuację
graniczną, gdy siła tarcia osiągnęła maksymalną wartość, a układ pozostaje
jeszcze w równowadze. Oznacza to, że wszystkie siły działające na pręt
równoważą się, a wypadkowy moment tych sił względem dowolnego punktu
wynosi 0. Warunek równowagi momentów sił względem punktu
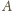 ma
postać
ma
postać
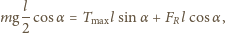
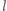 jest długością pręta. Uwzględniając, że
jest długością pręta. Uwzględniając, że
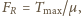 otrzymujemy
otrzymujemy
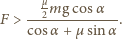
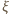 względem wierzchołka stożka. Równowaga
siły ciężkości i wyporu prowadzi do warunku
względem wierzchołka stożka. Równowaga
siły ciężkości i wyporu prowadzi do warunku
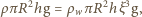
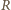 jest promieniem podstawy stożka,
jest promieniem podstawy stożka,
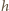 jego wysokością,
a
jego wysokością,
a
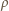 i
i
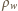 gęstościami odpowiednio lodu i wody. Stąd
gęstościami odpowiednio lodu i wody. Stąd
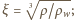 podstawiając
podstawiając
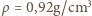 i
i
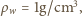 stwierdzamy,
że zanurzona część wysokości to
stwierdzamy,
że zanurzona część wysokości to
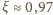 wysokości góry,
a zatem nad powierzchnię wystaje zaledwie około
wysokości góry,
a zatem nad powierzchnię wystaje zaledwie około
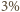 wysokości
góry.
wysokości
góry.
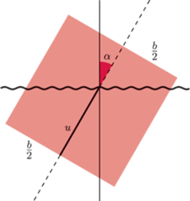
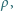 prostopadłościenny klocek o wymiarach
prostopadłościenny klocek o wymiarach
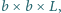 przy czym
przy czym
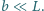 Zrobiono to tak zmyślnie, że najmniejsze ściany klocka mogą
ślizgać się bez tarcia po pionowych ścianach wanny, krawędzie o długości
Zrobiono to tak zmyślnie, że najmniejsze ściany klocka mogą
ślizgać się bez tarcia po pionowych ścianach wanny, krawędzie o długości
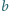 są pionowe lub poziome, a siła grawitacji działająca na klocek
równoważy siłę wyporu. Czy klocek jest w położeniu równowagi
trwałej?
są pionowe lub poziome, a siła grawitacji działająca na klocek
równoważy siłę wyporu. Czy klocek jest w położeniu równowagi
trwałej?
 i
i
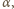 zaznaczone na rysunku.
zaznaczone na rysunku.
 możemy
wyrazić jako różnicę energii potencjalnej grawitacji, równej
możemy
wyrazić jako różnicę energii potencjalnej grawitacji, równej
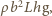 oraz energii potencjalnej, jaką miała wyparta przez klocek woda,
równej
oraz energii potencjalnej, jaką miała wyparta przez klocek woda,
równej
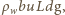 gdzie
gdzie
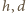 są odpowiednio wysokościami
środka ciężkości klocka i jego zanurzonej części nad poziomem wody.
Wielkości te są równe odpowiednio:
są odpowiednio wysokościami
środka ciężkości klocka i jego zanurzonej części nad poziomem wody.
Wielkości te są równe odpowiednio:
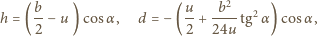
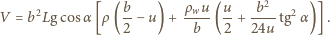
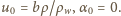 Dla małych wychyleń z położenia równowagi
mamy
Dla małych wychyleń z położenia równowagi
mamy
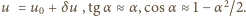 Podstawiając do
powyższego wzoru i ograniczając się do wyrazów kwadratowych
w
Podstawiając do
powyższego wzoru i ograniczając się do wyrazów kwadratowych
w
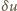 i
i
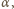 otrzymujemy:
otrzymujemy:
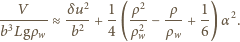
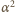 jest dodatni dla
jest dodatni dla
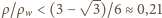 lub
lub
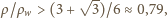 wtedy mamy do czynienia z minimum
energii potencjalnej i rozważana sytuacja odpowiada równowadze
trwałej.
wtedy mamy do czynienia z minimum
energii potencjalnej i rozważana sytuacja odpowiada równowadze
trwałej.
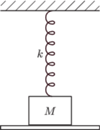
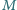 zawieszono na sprężynie o współczynniku
sprężystości
zawieszono na sprężynie o współczynniku
sprężystości
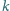 i położono na podstawce. W chwili początkowej
sprężyna była nieodkształcona. Podstawkę zaczęto opuszczać w dół
z przyspieszeniem
i położono na podstawce. W chwili początkowej
sprężyna była nieodkształcona. Podstawkę zaczęto opuszczać w dół
z przyspieszeniem
 Po jakim czasie ciężarek stracił kontakt
z podstawką? Jakie było maksymalne wydłużenie sprężyny?
Po jakim czasie ciężarek stracił kontakt
z podstawką? Jakie było maksymalne wydłużenie sprężyny?
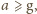 czyli przyspieszenie podstawki jest nie mniejsze od
przyspieszenia ziemskiego, ciężarek odrywa się od podstawki od razu. Zmiana
energii kinetycznej ciężarka po zakończeniu ruchu w dół wynosi 0 i równa
jest pracy sił ciężkości i sprężystości:
czyli przyspieszenie podstawki jest nie mniejsze od
przyspieszenia ziemskiego, ciężarek odrywa się od podstawki od razu. Zmiana
energii kinetycznej ciężarka po zakończeniu ruchu w dół wynosi 0 i równa
jest pracy sił ciężkości i sprężystości:
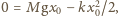 gdzie
gdzie
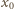 jest maksymalnym wydłużeniem sprężyny i wynosi
jest maksymalnym wydłużeniem sprężyny i wynosi
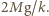
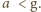 Równanie ruchu ciężarka, dopóki nie
straci on kontaktu z podstawką, ma postać
Równanie ruchu ciężarka, dopóki nie
straci on kontaktu z podstawką, ma postać
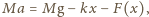 gdzie
gdzie
 jest wydłużeniem sprężyny, a
jest wydłużeniem sprężyny, a
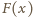 siłą reakcji
podstawki. W chwili oderwania, po przebyciu przez ciężarek drogi
siłą reakcji
podstawki. W chwili oderwania, po przebyciu przez ciężarek drogi
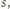 jest
jest
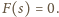 Stąd
Stąd
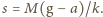 Z drugiej strony
Z drugiej strony
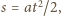 ponieważ do chwili oderwania ciężarek wraz z deską
porusza się ruchem jednostajnie przyspieszonym i szukany czas wynosi
ponieważ do chwili oderwania ciężarek wraz z deską
porusza się ruchem jednostajnie przyspieszonym i szukany czas wynosi
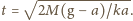 Prędkość ciężarka w chwili oderwania ma
wartość
Prędkość ciężarka w chwili oderwania ma
wartość
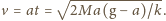 Od chwili oderwania ciężarek
porusza się ruchem harmonicznym.
Od chwili oderwania ciężarek
porusza się ruchem harmonicznym.
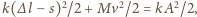 gdzie
gdzie
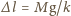 jest wydłużeniem sprężyny w stanie równowagi,
a
jest wydłużeniem sprężyny w stanie równowagi,
a
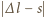 jest odległością od położenia równowagi w chwili oderwania,
wyznaczamy amplitudę drgań
jest odległością od położenia równowagi w chwili oderwania,
wyznaczamy amplitudę drgań
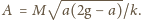 Maksymalne
wydłużenie sprężyny
Maksymalne
wydłużenie sprężyny
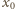 jest sumą wydłużenia w położeniu równowagi
jest sumą wydłużenia w położeniu równowagi
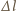 oraz amplitudy drgań
oraz amplitudy drgań