Zadanie ZF-948
o zadaniu...
- Publikacja w Delcie: marzec 2018
- Publikacja elektroniczna: 28 lutego 2018
Jony uranu U, znajdujące się w ciekłym cyrkonie 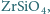 mieszają się z nim, podstawiając jony Zr, a jony ołowiu Pb nie reagują z cyrkonem i szybko dyfundują poza jego objętość. Po zestaleniu cyrkonu, dyfuzja praktycznie ustaje. W kryształach cyrkonu, znajdujących się w skale znalezionej w Zimbabwe, zmierzono, że stosunek liczby atomów ołowiu
mieszają się z nim, podstawiając jony Zr, a jony ołowiu Pb nie reagują z cyrkonem i szybko dyfundują poza jego objętość. Po zestaleniu cyrkonu, dyfuzja praktycznie ustaje. W kryształach cyrkonu, znajdujących się w skale znalezionej w Zimbabwe, zmierzono, że stosunek liczby atomów ołowiu 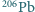 do liczby atomów uranu
do liczby atomów uranu 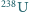 wynosi
wynosi 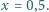 Jaki jest wiek tej skały, jeśli w serii kolejnych rozpadów alfa i beta,
Jaki jest wiek tej skały, jeśli w serii kolejnych rozpadów alfa i beta, 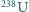 rozpada się do
rozpada się do 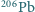 z czasem połowicznego zaniku
z czasem połowicznego zaniku 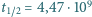 lat?
lat?
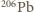 znajdowane w skale pochodzą więc z późniejszych rozpadów jonów
znajdowane w skale pochodzą więc z późniejszych rozpadów jonów 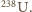 Niech
Niech 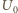 oznacza początkową liczbę jonów
oznacza początkową liczbę jonów 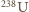 w próbce. Ich liczba po czasie
w próbce. Ich liczba po czasie 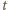 wynosi
wynosi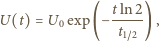
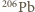 wynosi
wynosi 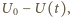 bo wszystkie powstały w wyniku rozpadu
bo wszystkie powstały w wyniku rozpadu 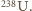 Stosunek liczby jonów
Stosunek liczby jonów 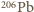 do liczby jonów
do liczby jonów 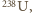 wynosi więc
wynosi więc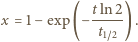
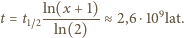
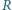 rośnie z liczbą
rośnie z liczbą 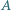 nukleonów jak
nukleonów jak 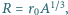 gdzie
gdzie 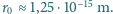 Korzystając z zasady nieoznaczoności, oszacuj na tej podstawie średnią energię
Korzystając z zasady nieoznaczoności, oszacuj na tej podstawie średnią energię 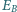 wiązania nukleonu w jądrze. Masa nukleonu
wiązania nukleonu w jądrze. Masa nukleonu 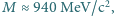 a iloczyn
a iloczyn 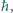 tj. stałej Plancka podzielonej przez
tj. stałej Plancka podzielonej przez 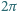 i prędkości światła
i prędkości światła  wynosi
wynosi 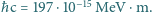
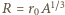 wynika, że objętość jądra jest proporcjonalna do liczby nukleonów, a więc średnio, na każdy nukleon przypada objętość kuli o promieniu
wynika, że objętość jądra jest proporcjonalna do liczby nukleonów, a więc średnio, na każdy nukleon przypada objętość kuli o promieniu 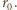 Tym samym możemy przyjąć, że nieoznaczoność każdej ze współrzędnych nukleonu wynosi
Tym samym możemy przyjąć, że nieoznaczoność każdej ze współrzędnych nukleonu wynosi 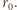 Zgodnie z zasadą nieoznaczoności dla współrzędnej
Zgodnie z zasadą nieoznaczoności dla współrzędnej 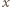 mamy
mamy 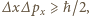 gdzie
gdzie 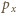 oznacza pęd w kierunku
oznacza pęd w kierunku 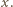 Analogiczne nierówności spełnione są dla współrzędnych i pędów w kierunkach
Analogiczne nierówności spełnione są dla współrzędnych i pędów w kierunkach 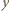 i
i 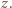 Pozwala to wyznaczyć nieoznaczoność pędu w każdym z kierunków
Pozwala to wyznaczyć nieoznaczoność pędu w każdym z kierunków 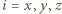 :
: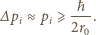
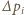 z jego wartością
z jego wartością 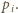 Dla energii kinetycznej
Dla energii kinetycznej 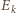 ruchu nukleonu otrzymujemy:
ruchu nukleonu otrzymujemy: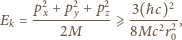
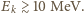 Wartość średniej energii wiązania
Wartość średniej energii wiązania 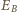 nukleonu musi być większa od jego energii kinetycznej. Otrzymujemy oszacowanie
nukleonu musi być większa od jego energii kinetycznej. Otrzymujemy oszacowanie 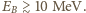 Dla ciężkich jąder mierzona średnia energia wiązania na nukleon wynosi około
Dla ciężkich jąder mierzona średnia energia wiązania na nukleon wynosi około 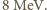
 wisi na nici. Na jaką najmniejszą wysokość należy podnieść ciężarek, aby spadając, rozerwał nić? Minimalna siła wystarczająca do rozerwania nici wynosi
wisi na nici. Na jaką najmniejszą wysokość należy podnieść ciężarek, aby spadając, rozerwał nić? Minimalna siła wystarczająca do rozerwania nici wynosi 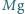 (
( 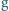 jest przyspieszeniem ziemskim) i przed rozerwaniem wydłuża ją o
jest przyspieszeniem ziemskim) i przed rozerwaniem wydłuża ją o  Zakładamy, że siła naprężenia nici jest proporcjonalna do jej wydłużenia aż do zerwania.
Zakładamy, że siła naprężenia nici jest proporcjonalna do jej wydłużenia aż do zerwania.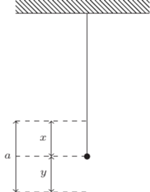
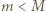 . Oznaczmy przez
. Oznaczmy przez 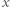 wydłużenie nici w stanie równowagi, mamy wtedy związki:
wydłużenie nici w stanie równowagi, mamy wtedy związki: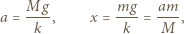
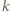 jest współczynnikiem sprężystości nici. Dodatkowe wydłużenie w momencie rozerwania nici wynosi
jest współczynnikiem sprężystości nici. Dodatkowe wydłużenie w momencie rozerwania nici wynosi 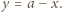
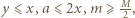 na ciężarek cały czas działa siła sprężystości i aż do momentu zerwania nici porusza się on ruchem harmonicznym. Najmniejsza wysokość, na jaką musimy go podnieść, wynosi
na ciężarek cały czas działa siła sprężystości i aż do momentu zerwania nici porusza się on ruchem harmonicznym. Najmniejsza wysokość, na jaką musimy go podnieść, wynosi 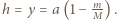
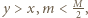 możemy skorzystać z zasady zachowania energii:
możemy skorzystać z zasady zachowania energii: 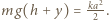
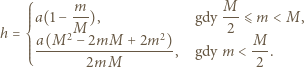

 i zewnętrznym
i zewnętrznym 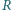 nawinięta jest linka. Koniec A linki ciągnięty jest poziomo z prędkością
nawinięta jest linka. Koniec A linki ciągnięty jest poziomo z prędkością  Na szpuli opiera się deska, która może obracać się wokół poziomej osi prostopadłej do płaszczyzny rysunku, przechodzącej przez punkt O. Szpula toczy się bez poślizgu po powierzchni poziomej. Jaka jest prędkość kątowa deski, gdy tworzy ona z poziomem kąt
Na szpuli opiera się deska, która może obracać się wokół poziomej osi prostopadłej do płaszczyzny rysunku, przechodzącej przez punkt O. Szpula toczy się bez poślizgu po powierzchni poziomej. Jaka jest prędkość kątowa deski, gdy tworzy ona z poziomem kąt 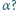
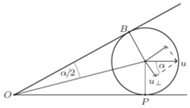
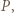 stąd prędkość kątowa ruchu obrotowego szpuli dana jest wzorem
stąd prędkość kątowa ruchu obrotowego szpuli dana jest wzorem 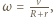 a jej prędkość ruchu postępowego wynosi
a jej prędkość ruchu postępowego wynosi 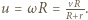 Prędkość punktu
Prędkość punktu 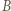 styczności szpuli z deską w chwili, gdy deska tworzy z poziomem kąt
styczności szpuli z deską w chwili, gdy deska tworzy z poziomem kąt 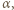 ma składową prostopadłą do deski
ma składową prostopadłą do deski 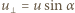 (prędkość ruchu obrotowego jest prostopadła do deski). Odległość punktu
(prędkość ruchu obrotowego jest prostopadła do deski). Odległość punktu 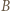 od osi obrotu deski wynosi
od osi obrotu deski wynosi 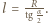 Szukana prędkość kątowa deski dana jest wzorem
Szukana prędkość kątowa deski dana jest wzorem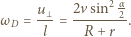
 i powtarzał jej pomiar w równych odstępach czasu. Dziesiątemu i jedenastemu pomiarowi odpowiadały odpowiednio temperatury
i powtarzał jej pomiar w równych odstępach czasu. Dziesiątemu i jedenastemu pomiarowi odpowiadały odpowiednio temperatury 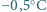 i
i 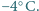 Jaki ułamek masy mokrego śniegu stanowiła woda? Ciepło właściwe lodu
Jaki ułamek masy mokrego śniegu stanowiła woda? Ciepło właściwe lodu  wynosi
wynosi 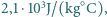 a ciepło topnienia lodu
a ciepło topnienia lodu 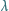 wynosi
wynosi 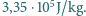
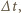 to temperatura śniegu wyniosła
to temperatura śniegu wyniosła 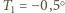 po czasie
po czasie 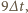 a
a 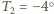 po czasie
po czasie 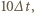 przy czym po czasie
przy czym po czasie 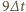 cała zawarta w śniegu woda była już zamarznięta. Zapiszemy bilans cieplny, przyjmując, że prędkość odprowadzania ciepła w zamrażarce jest stała:
cała zawarta w śniegu woda była już zamarznięta. Zapiszemy bilans cieplny, przyjmując, że prędkość odprowadzania ciepła w zamrażarce jest stała: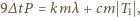
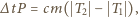
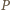 jest energią odprowadzaną w jednostce czasu,
jest energią odprowadzaną w jednostce czasu,  jest masą śniegu, a
jest masą śniegu, a 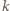 określa ułamek masy wody w śniegu.
określa ułamek masy wody w śniegu.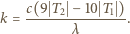
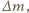 która wyparuje w ciągu bardzo małego czasu
która wyparuje w ciągu bardzo małego czasu 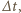 przy stałej temperaturze, stałej wilgotności powietrza i braku wiatru, zależy tylko od pola powierzchni wody
przy stałej temperaturze, stałej wilgotności powietrza i braku wiatru, zależy tylko od pola powierzchni wody 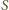 :
: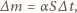
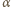 jest współczynnikiem proporcjonalności. Zmiana poziomu wody
jest współczynnikiem proporcjonalności. Zmiana poziomu wody 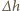 jest związana z
jest związana z 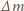 zależnością
zależnością 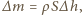 gdzie
gdzie 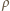 to gęstość wody. Stąd
to gęstość wody. Stąd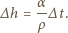
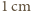 , to całkowicie wyparuje ona z naczynia po 30 dobach.
, to całkowicie wyparuje ona z naczynia po 30 dobach.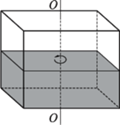
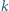 -ta część powierzchni dna. Jak zmieniła się w wyniku tego siła parcia na dno i wąskie ścianki boczne (w porównaniu z przypadkiem nieruchomego naczynia)? Ciecz nie wylewa się z naczynia. Napięcie powierzchniowe można zaniedbać.
-ta część powierzchni dna. Jak zmieniła się w wyniku tego siła parcia na dno i wąskie ścianki boczne (w porównaniu z przypadkiem nieruchomego naczynia)? Ciecz nie wylewa się z naczynia. Napięcie powierzchniowe można zaniedbać.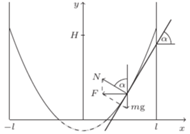
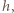 a rozmiary podstawy naczynia przez
a rozmiary podstawy naczynia przez 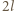 i
i 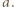 Zgodnie z treścią zadania
Zgodnie z treścią zadania 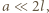 możemy więc przyjąć, że powierzchnia cieczy w obracającym się naczyniu ma kształt jak na rysunku.
możemy więc przyjąć, że powierzchnia cieczy w obracającym się naczyniu ma kształt jak na rysunku.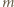 na jej powierzchni w obracającym się naczyniu. Działa na niego siła ciężkości
na jej powierzchni w obracającym się naczyniu. Działa na niego siła ciężkości 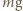 i siła reakcji
i siła reakcji 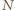 ze strony pozostałej cieczy, prostopadła do jej powierzchni. Wypadkowa tych dwóch sił jest siłą dośrodkową o wartości
ze strony pozostałej cieczy, prostopadła do jej powierzchni. Wypadkowa tych dwóch sił jest siłą dośrodkową o wartości 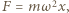 gdzie
gdzie 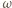 jest prędkością kątową, a
jest prędkością kątową, a 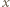 odległością elementu cieczy od osi obrotu. Styczna do powierzchni cieczy w badanym punkcie nachylona jest do poziomu pod kątem
odległością elementu cieczy od osi obrotu. Styczna do powierzchni cieczy w badanym punkcie nachylona jest do poziomu pod kątem  i spełnione są związki:
i spełnione są związki: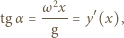
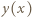 opisuje kształt powierzchni cieczy. Stąd
opisuje kształt powierzchni cieczy. Stąd 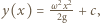 a stałą
a stałą  możemy wyznaczyć z warunków brzegowych. Gdy
możemy wyznaczyć z warunków brzegowych. Gdy 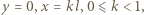 zatem
zatem 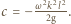 Ponieważ ciecz jest nieściśliwa i jej objętość stała, możemy wyznaczyć prędkość kątową obracającego się naczynia, przyrównując objętość cieczy w połówce naczynia spoczywającego i obracającego się:
Ponieważ ciecz jest nieściśliwa i jej objętość stała, możemy wyznaczyć prędkość kątową obracającego się naczynia, przyrównując objętość cieczy w połówce naczynia spoczywającego i obracającego się: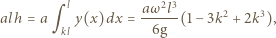
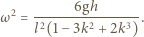
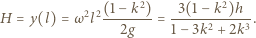
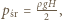 gdzie
gdzie 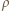 jest gęstością cieczy. Szukany stosunek parć na ściankę boczną w obracającym się i nieruchomym naczyniu równy jest
jest gęstością cieczy. Szukany stosunek parć na ściankę boczną w obracającym się i nieruchomym naczyniu równy jest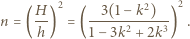
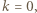 otrzymujemy
otrzymujemy 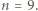
 w jednorodnym polu magnetycznym o indukcji
w jednorodnym polu magnetycznym o indukcji 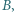 równoległym do powierzchni Ziemi. Płaszczyzna płytki jest równoległa do linii pola magnetycznego i prostopadła do powierzchni Ziemi. Grubość płytki
równoległym do powierzchni Ziemi. Płaszczyzna płytki jest równoległa do linii pola magnetycznego i prostopadła do powierzchni Ziemi. Grubość płytki 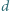 jest dużo mniejsza od jej promienia
jest dużo mniejsza od jej promienia 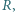 przyspieszenie ziemskie ma wartość
przyspieszenie ziemskie ma wartość 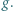
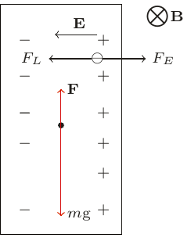
 Na swobodne elektrony w płytce działa w polu magnetycznym siła Lorentza
Na swobodne elektrony w płytce działa w polu magnetycznym siła Lorentza 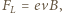 gdzie
gdzie  jest wartością bezwzględną ładunku elektronu. W wyniku tego elektrony przemieszczają się na lewą stronę płytki. Powoduje to powstanie pola elektrycznego
jest wartością bezwzględną ładunku elektronu. W wyniku tego elektrony przemieszczają się na lewą stronę płytki. Powoduje to powstanie pola elektrycznego 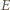 skierowanego jak na rysunku. Elektrony przestają się przemieszczać, gdy siła Lorentza zostaje zrównoważona przez siłę elektryczną
skierowanego jak na rysunku. Elektrony przestają się przemieszczać, gdy siła Lorentza zostaje zrównoważona przez siłę elektryczną 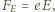 czyli zachodzi związek
czyli zachodzi związek 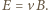 Ponieważ grubość płytki jest dużo mniejsza od jej promienia, możemy ją traktować jako kondensator płaski, w którym napięcie między powierzchniami wynosi
Ponieważ grubość płytki jest dużo mniejsza od jej promienia, możemy ją traktować jako kondensator płaski, w którym napięcie między powierzchniami wynosi 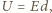 a ładunek na powierzchniach
a ładunek na powierzchniach 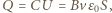 gdzie
gdzie 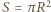 jest powierzchnią płytki. Gdy prędkość płytki rośnie, zmieniają się ładunki na jej powierzchniach, czyli przez płytkę płynie prąd o natężeniu
jest powierzchnią płytki. Gdy prędkość płytki rośnie, zmieniają się ładunki na jej powierzchniach, czyli przez płytkę płynie prąd o natężeniu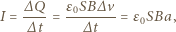
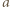 jest przyspieszeniem płytki. Na przewodnik z prądem w polu magnetycznym działa siła elektrodynamiczna, która w naszym przypadku ma zwrot pionowo w górę i wartość
jest przyspieszeniem płytki. Na przewodnik z prądem w polu magnetycznym działa siła elektrodynamiczna, która w naszym przypadku ma zwrot pionowo w górę i wartość 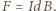 Równanie ruchu płytki ma postać
Równanie ruchu płytki ma postać 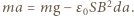 Stąd szukane przyspieszenie jest równe
Stąd szukane przyspieszenie jest równe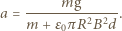
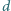 i przenikalności dielektrycznej
i przenikalności dielektrycznej  Na warstwie dielektryka umieszczono kroplę przewodzącej cieczy (elektrolitu) niezwilżającej dielektryka. Jak zmieni się kąt zwilżania
Na warstwie dielektryka umieszczono kroplę przewodzącej cieczy (elektrolitu) niezwilżającej dielektryka. Jak zmieni się kąt zwilżania 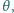 gdy do kropli przyłożymy napięcie
gdy do kropli przyłożymy napięcie 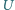 względem metalowej elektrody? Napięcia powierzchniowe wynoszą: ciecz-dielektryk
względem metalowej elektrody? Napięcia powierzchniowe wynoszą: ciecz-dielektryk 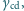 ciecz-gaz otaczający układ
ciecz-gaz otaczający układ 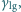 a dielektryk-gaz
a dielektryk-gaz 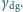
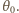 Mamy więc:
Mamy więc: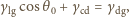
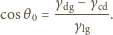
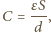 gdzie
gdzie 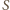 oznacza pole powierzchni styku kropli z dielektrykiem. Energia kondensatora naładowanego do napięcia
oznacza pole powierzchni styku kropli z dielektrykiem. Energia kondensatora naładowanego do napięcia 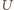 wynosi
wynosi 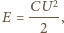 ale trzeba też uwzględnić, że podczas ładowania, źródło napięcia wykonuje pracę potrzebną do pokonania stałego napięcia
ale trzeba też uwzględnić, że podczas ładowania, źródło napięcia wykonuje pracę potrzebną do pokonania stałego napięcia 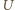 przez przenoszony ładunek
przez przenoszony ładunek 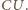 Całkowita zmiana energii układu źródło-kondensator wynosi więc:
Całkowita zmiana energii układu źródło-kondensator wynosi więc: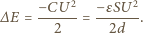
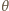 będzie teraz spełniał zależność:
będzie teraz spełniał zależność: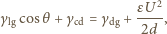
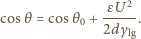
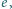 do jego masy
do jego masy 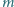 metodą, w której metaliczne próbki poddawali przyspieszeniom. Wyjaśnij, jak to było możliwe. Przyjmij model swobodnych elektronów w metalu.
metodą, w której metaliczne próbki poddawali przyspieszeniom. Wyjaśnij, jak to było możliwe. Przyjmij model swobodnych elektronów w metalu.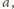 to elektrony przewodnictwa (przyjmujemy, że wewnątrz metalu zachowują się jak cząstki swobodne) doznają względem sieci krystalicznej metalu przyspieszenia
to elektrony przewodnictwa (przyjmujemy, że wewnątrz metalu zachowują się jak cząstki swobodne) doznają względem sieci krystalicznej metalu przyspieszenia 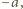 co odpowiada ruchowi w polu elektrycznym
co odpowiada ruchowi w polu elektrycznym 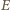 :
: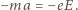
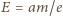 wywołuje przepływ prądu o gęstości
wywołuje przepływ prądu o gęstości 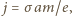 gdzie
gdzie 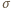 oznacza przewodnictwo właściwe metalu. Wartość tego prądu można zmierzyć i (zmierzywszy również przyspieszenie i przewodnictwo właściwe) wyznaczyć żądany stosunek:
oznacza przewodnictwo właściwe metalu. Wartość tego prądu można zmierzyć i (zmierzywszy również przyspieszenie i przewodnictwo właściwe) wyznaczyć żądany stosunek: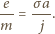
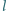 od siebie i puszczono swobodnie. Po czasie
od siebie i puszczono swobodnie. Po czasie 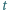 odległość między nimi wzrosła dwukrotnie. Po jakim czasie wzrośnie dwukrotnie odległość między tymi kulkami, gdy ich odległość początkowa będzie wynosić
odległość między nimi wzrosła dwukrotnie. Po jakim czasie wzrośnie dwukrotnie odległość między tymi kulkami, gdy ich odległość początkowa będzie wynosić 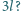
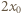 i obliczmy ich prędkości
i obliczmy ich prędkości 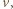 gdy odległość ta osiągnie wartość
gdy odległość ta osiągnie wartość 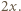 Z zasady zachowania energii otrzymujemy
Z zasady zachowania energii otrzymujemy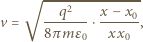
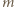 jest masą, a
jest masą, a 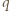 ładunkiem kulki.
ładunkiem kulki.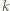 oraz położenia początkowego
oraz położenia początkowego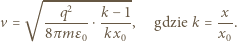
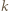 zmienia się od 1 do 2. Podzielmy przemieszczenia kulek w obu rozważanych przypadkach na jednakową liczbę odcinków, dla których
zmienia się od 1 do 2. Podzielmy przemieszczenia kulek w obu rozważanych przypadkach na jednakową liczbę odcinków, dla których 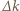 są takie same. Przemieszczenie kulki przy zmianie
są takie same. Przemieszczenie kulki przy zmianie 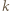 o
o 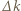 wynosi
wynosi 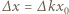 i w drugim przypadku jest 3 razy większe niż w pierwszym:
i w drugim przypadku jest 3 razy większe niż w pierwszym: 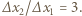 Z
Z 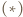 wynika, że dla danego
wynika, że dla danego 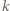 prędkość kulki w pierwszym przypadku jest
prędkość kulki w pierwszym przypadku jest 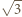 razy większa niż w drugim. Przy zmianie
razy większa niż w drugim. Przy zmianie 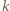 o małe
o małe 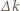 średnie prędkości kulek również będą różnić się
średnie prędkości kulek również będą różnić się 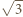 razy:
razy: 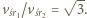 Czasy, w których kulki przemieszczają się o
Czasy, w których kulki przemieszczają się o 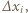 są równe:
są równe: 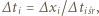 gdzie
gdzie 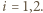 Stosunek tych czasów w rozważanych przypadkach dany jest wzorem
Stosunek tych czasów w rozważanych przypadkach dany jest wzorem 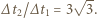 Całkowity czas ruchu w drugim przypadku wynosi
Całkowity czas ruchu w drugim przypadku wynosi 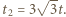
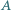 porusza się z prędkością
porusza się z prędkością 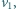 goni go pojazd
goni go pojazd 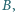 poruszający się w tym samym kierunku z prędkością
poruszający się w tym samym kierunku z prędkością 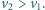 W chwili początkowej odległość między pojazdami wynosi
W chwili początkowej odległość między pojazdami wynosi 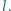 Po jakim czasie pojazd
Po jakim czasie pojazd 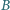 dogoni
dogoni  z punktu widzenia obserwatora na Ziemi oraz z punktu widzenia kosmonauty w pojeździe
z punktu widzenia obserwatora na Ziemi oraz z punktu widzenia kosmonauty w pojeździe 
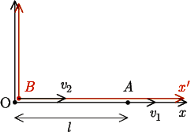
 zsynchronizowali swoje zegary, gdy znajdowali się w tym samym miejscu i tę chwilę uznali za zerową. Zdarzeniem początkowym jest odbicie sygnału radarowego wysłanego z Ziemi od pojazdu
zsynchronizowali swoje zegary, gdy znajdowali się w tym samym miejscu i tę chwilę uznali za zerową. Zdarzeniem początkowym jest odbicie sygnału radarowego wysłanego z Ziemi od pojazdu 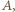 któremu obserwator O przypisuje współrzędną czasową
któremu obserwator O przypisuje współrzędną czasową 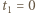 oraz współrzędną przestrzenną
oraz współrzędną przestrzenną 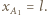 W układzie statku
W układzie statku 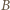 to samo zdarzenie zachodzi w chwili
to samo zdarzenie zachodzi w chwili 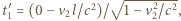 w miejscu o współrzędnej przestrzennej
w miejscu o współrzędnej przestrzennej 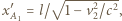 zgodnie z transformacją Lorentza.
zgodnie z transformacją Lorentza.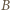 dogania
dogania 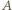 - zachodzi w układzie Ziemi w miejscu o współrzędnej
- zachodzi w układzie Ziemi w miejscu o współrzędnej 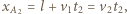 stąd chwila zdarzenia wynosi
stąd chwila zdarzenia wynosi 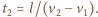 W układzie statku
W układzie statku 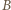 miejsce zdarzenia ma współrzędną
miejsce zdarzenia ma współrzędną 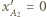 i zachodzi w chwili
i zachodzi w chwili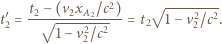
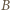 dogoni
dogoni 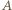 po czasie
po czasie 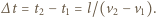
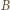 szukany czas wynosi
szukany czas wynosi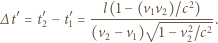
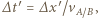 gdzie
gdzie 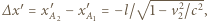 a
a 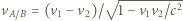 jest prędkością statku
jest prędkością statku 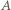 względem
względem 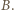
 w jednakowych odległościach jedna za drugą (odległość przednich zderzaków kolejnych ciężarówek wynosi
w jednakowych odległościach jedna za drugą (odległość przednich zderzaków kolejnych ciężarówek wynosi 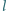 ). Jeżeli samochód osobowy jedzie z prędkością
). Jeżeli samochód osobowy jedzie z prędkością 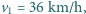 to co
to co 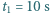 jest wyprzedzany przez ciężarówkę, a jeżeli jedzie z prędkością
jest wyprzedzany przez ciężarówkę, a jeżeli jedzie z prędkością 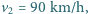 to on co
to on co 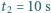 wyprzedza ciężarówkę. Co ile sekund ciężarówki będą mijać samochód osobowy, jeżeli zatrzyma się on na poboczu?
wyprzedza ciężarówkę. Co ile sekund ciężarówki będą mijać samochód osobowy, jeżeli zatrzyma się on na poboczu?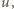 a odległość przednich zderzaków kolejnych ciężarówek wynosi
a odległość przednich zderzaków kolejnych ciężarówek wynosi 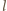 to
to 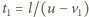 i
i 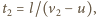 gdzie
gdzie 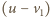 i
i 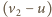 są względnymi prędkościami samochodu osobowego i kolumny w przypadku (1) i (2). Stąd
są względnymi prędkościami samochodu osobowego i kolumny w przypadku (1) i (2). Stąd 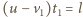 oraz
oraz 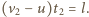 Rozwiązując ten układ równań dostajemy:
Rozwiązując ten układ równań dostajemy: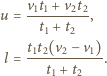
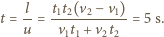
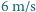 w korku spada do średniej wartości
w korku spada do średniej wartości 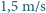 (czas włączenia żółtego światła pomijamy). W celu zmniejszenia korka czas włączenia zielonego światła podwojono, nie zmieniając czasu włączenia światła czerwonego. Ile wyniesie średnia prędkość samochodów w korku, jeżeli ich normalna prędkość nie ulegnie zmianie?
(czas włączenia żółtego światła pomijamy). W celu zmniejszenia korka czas włączenia zielonego światła podwojono, nie zmieniając czasu włączenia światła czerwonego. Ile wyniesie średnia prędkość samochodów w korku, jeżeli ich normalna prędkość nie ulegnie zmianie?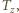 gdy włączone jest zielone światło, obok sygnalizatora przejeżdża część korka o długości
gdy włączone jest zielone światło, obok sygnalizatora przejeżdża część korka o długości 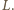 Na czas
Na czas 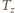 składa się czas potrzebny na to, aby "fala" przebyła drogę
składa się czas potrzebny na to, aby "fala" przebyła drogę 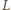 i czas potrzebny, aby samochód drogę
i czas potrzebny, aby samochód drogę 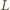 przejechał. Jeżeli
przejechał. Jeżeli  jest prędkością samochodu (bez uwzględniania jego rozpędzania się), a
jest prędkością samochodu (bez uwzględniania jego rozpędzania się), a  prędkością rozchodzenia się "fali", to
prędkością rozchodzenia się "fali", to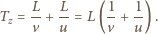
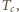 to średnia prędkość poruszania się w korku wynosi
to średnia prędkość poruszania się w korku wynosi 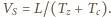 Podstawiając, znajdujemy
Podstawiając, znajdujemy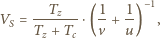
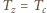 otrzymujemy
otrzymujemy 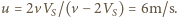 Po podwojeniu czasu
Po podwojeniu czasu 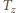 prędkość samochodu w korku wyniesie:
prędkość samochodu w korku wyniesie: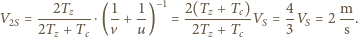
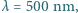 padająca prostopadle na płytkę, ogniskuje się w odległości
padająca prostopadle na płytkę, ogniskuje się w odległości 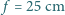 od płytki. Rozmiary płytki są małe w porównaniu z odległością
od płytki. Rozmiary płytki są małe w porównaniu z odległością 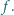
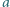 od płytki na jej osi przechodzącej przez środki pierścieni?
od płytki na jej osi przechodzącej przez środki pierścieni?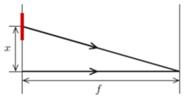
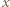 od centrum płytki do środka ekranu umieszczonego w odległości
od centrum płytki do środka ekranu umieszczonego w odległości 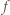 od płytki wynosi:
od płytki wynosi: 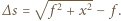 W przybliżeniu
W przybliżeniu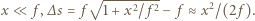
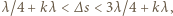 gdzie
gdzie 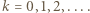 Stąd
Stąd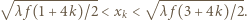
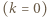 ma promień wewnętrzny
ma promień wewnętrzny 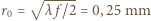 , zewnętrzny
, zewnętrzny 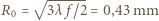 , drugi
, drugi 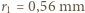 ,
, 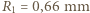 . b) niech szukana odległość wynosi
. b) niech szukana odległość wynosi 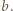 Chcemy, żeby różnica dróg promieni przechodzących przez punkt odległy o
Chcemy, żeby różnica dróg promieni przechodzących przez punkt odległy o  od środka płytki i przechodzących przez środek płytki była taka sama, jak w przypadku wiązki równoległej:
od środka płytki i przechodzących przez środek płytki była taka sama, jak w przypadku wiązki równoległej: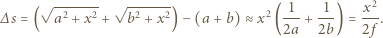
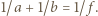

 na zbocze nachylone pod kątem
na zbocze nachylone pod kątem  do poziomu (rysunek) i ciągnie sanki o masie
do poziomu (rysunek) i ciągnie sanki o masie 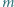 za pomocą nierozciągliwej, lekkiej linki o długości
za pomocą nierozciągliwej, lekkiej linki o długości 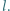 Sanki ślizgają się bez tarcia po powierzchni poziomej. Jakie jest naprężenie linki, gdy tworzy ona z poziomem kąt
Sanki ślizgają się bez tarcia po powierzchni poziomej. Jakie jest naprężenie linki, gdy tworzy ona z poziomem kąt 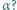
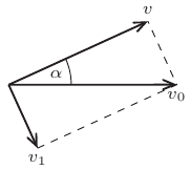
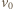 jest pozioma, możemy rozłożyć ją na składowe
jest pozioma, możemy rozłożyć ją na składowe  równoległą do linki i
równoległą do linki i 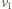 prostopadłą do linki. Zachodzi związek
prostopadłą do linki. Zachodzi związek 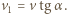 W układzie inercjalnym, związanym z człowiekiem, sanki poruszają się po okręgu o promieniu
W układzie inercjalnym, związanym z człowiekiem, sanki poruszają się po okręgu o promieniu 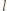 z prędkością
z prędkością 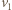 i przyspieszeniem dośrodkowym
i przyspieszeniem dośrodkowym 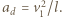 Jedyną siłą działającą na sanki w kierunku poziomym jest składowa siły naprężenia linki
Jedyną siłą działającą na sanki w kierunku poziomym jest składowa siły naprężenia linki 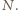 Nadaje ona sankom przyspieszenie
Nadaje ona sankom przyspieszenie 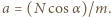 Składowa tego przyspieszenia równoległa do linki jest przyspieszeniem dośrodkowym:
Składowa tego przyspieszenia równoległa do linki jest przyspieszeniem dośrodkowym: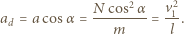
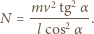
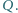 Pierścień spoczywa na poziomej, gładkiej powierzchni, a cały układ znajduje się wewnątrz bardzo długiej cewki prostopadłej do płaszczyzny pierścienia. Ile wyniesie końcowa prędkość kątowa
Pierścień spoczywa na poziomej, gładkiej powierzchni, a cały układ znajduje się wewnątrz bardzo długiej cewki prostopadłej do płaszczyzny pierścienia. Ile wyniesie końcowa prędkość kątowa 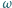 pierścienia, gdy wewnątrz cewki indukcja pola magnetycznego wzrośnie od zera do wartości
pierścienia, gdy wewnątrz cewki indukcja pola magnetycznego wzrośnie od zera do wartości 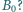
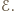 Zgodnie z prawem indukcji Faradaya mamy
Zgodnie z prawem indukcji Faradaya mamy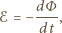
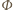 oznacza strumień indukcji przez powierzchnię cewki. Oznacza to, że w każdym punkcie pierścienia, stycznie do niego, na ładunki działa pole elektryczne o wartości
oznacza strumień indukcji przez powierzchnię cewki. Oznacza to, że w każdym punkcie pierścienia, stycznie do niego, na ładunki działa pole elektryczne o wartości 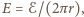 gdzie
gdzie  jest promieniem pierścienia. Liniowa gęstość ładunku na pierścieniu wynosi
jest promieniem pierścienia. Liniowa gęstość ładunku na pierścieniu wynosi 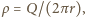 a więc na odcinek
a więc na odcinek 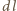 pierścienia działa siła
pierścienia działa siła 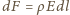 i moment siły względem jego środka to
i moment siły względem jego środka to 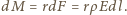 Całkowity moment siły "obracający" pierścień wynosi
Całkowity moment siły "obracający" pierścień wynosi 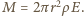 Ten moment siły nadaje pierścieniowi przyspieszenie kątowe
Ten moment siły nadaje pierścieniowi przyspieszenie kątowe 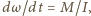 gdzie
gdzie 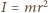 jest momentem bezwładności pierścienia. Otrzymujemy więc
jest momentem bezwładności pierścienia. Otrzymujemy więc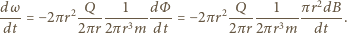
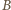 przez pole koła. Po uproszczeniu powtarzających się czynników dostajemy:
przez pole koła. Po uproszczeniu powtarzających się czynników dostajemy: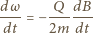
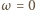 oraz
oraz 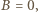 ostatecznie otrzymujemy
ostatecznie otrzymujemy 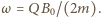
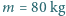 i wzroście
i wzroście 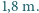 Dla uproszczenia załóż, że podczas całego "lotu" powietrze ma stałą gęstość w przybliżeniu równą gęstości przy ziemi i temperaturę około
Dla uproszczenia załóż, że podczas całego "lotu" powietrze ma stałą gęstość w przybliżeniu równą gęstości przy ziemi i temperaturę około 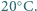 Stała gazowa
Stała gazowa 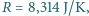 ciśnienie atmosferyczne
ciśnienie atmosferyczne 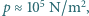 średnia masa molowa cząsteczek powietrza
średnia masa molowa cząsteczek powietrza 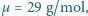 przyspieszenie ziemskie
przyspieszenie ziemskie 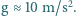
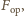 z jaką powietrze działa na ciało poruszające się z prędkością
z jaką powietrze działa na ciało poruszające się z prędkością  wynosi
wynosi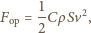
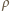 jest gęstością powietrza,
jest gęstością powietrza, 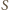 polem powierzchni przekroju ciała (prostopadłego do kierunku ruchu), a
polem powierzchni przekroju ciała (prostopadłego do kierunku ruchu), a 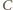 współczynnikiem zależnym od kształtu ciała o wartości rzędu 1 (od
współczynnikiem zależnym od kształtu ciała o wartości rzędu 1 (od 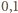 do 1). W dobrym przybliżeniu powietrze spełnia równanie stanu gazu doskonałego. Korzystając z tego równania dla danych zadania, otrzymujemy (dla temperatury w skali Kelvina
do 1). W dobrym przybliżeniu powietrze spełnia równanie stanu gazu doskonałego. Korzystając z tego równania dla danych zadania, otrzymujemy (dla temperatury w skali Kelvina 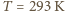 ):
):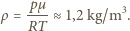
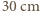 - w ramionach na pewno więcej, ale za to dla nóg mniej, co dla wzrostu
- w ramionach na pewno więcej, ale za to dla nóg mniej, co dla wzrostu 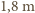 daje
daje 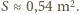 Maksymalna prędkość odpowiada sytuacji, gdy siła oporu
Maksymalna prędkość odpowiada sytuacji, gdy siła oporu 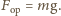 Po podstawieniu powyższych oszacowań do równania otrzymujemy
Po podstawieniu powyższych oszacowań do równania otrzymujemy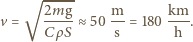
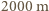 po około
po około 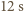 skoczkowie osiągają stałe prędkości około
skoczkowie osiągają stałe prędkości około 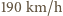 bliskie otrzymanej w rozwiązaniu.
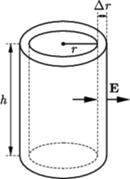
bliskie otrzymanej w rozwiązaniu.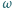 wokół swojej osi. Walec umieszczony jest w jednorodnym polu magnetycznym, którego wektor indukcji
wokół swojej osi. Walec umieszczony jest w jednorodnym polu magnetycznym, którego wektor indukcji 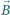 jest równoległy do osi walca. Znaleźć gęstość ładunku wewnątrz walca.
jest równoległy do osi walca. Znaleźć gęstość ładunku wewnątrz walca.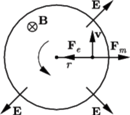
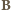 oraz prędkości kątowej walca
oraz prędkości kątowej walca 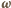 mają zwroty przeciwne (
mają zwroty przeciwne (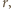 działa siła magnetyczna
działa siła magnetyczna 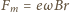 zwrócona na zewnątrz okręgu (
zwrócona na zewnątrz okręgu (  oznacza wartość bezwzględną ładunku elektronu). Wypadkowa siła działająca na elektron jest siłą dośrodkową, zatem siła elektryczna
oznacza wartość bezwzględną ładunku elektronu). Wypadkowa siła działająca na elektron jest siłą dośrodkową, zatem siła elektryczna 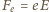 jest większa od siły magnetycznej i ma zwrot do środka okręgu (
jest większa od siły magnetycznej i ma zwrot do środka okręgu ( 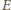 jest natężeniem pola elektrycznego wewnątrz walca). Równanie ruchu elektronu ma postać
jest natężeniem pola elektrycznego wewnątrz walca). Równanie ruchu elektronu ma postać 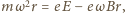 stąd natężenie pola elektrycznego
stąd natężenie pola elektrycznego 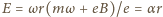 ma zwrot na zewnątrz walca, a jego wartość rośnie liniowo z odległością od środka walca. Rozważmy cienką warstwę cylindryczną o grubości
ma zwrot na zewnątrz walca, a jego wartość rośnie liniowo z odległością od środka walca. Rozważmy cienką warstwę cylindryczną o grubości 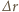 wewnątrz walca (
wewnątrz walca (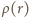 gęstość ładunku wewnątrz tej warstwy, możemy zapisać prawo Gaussa
gęstość ładunku wewnątrz tej warstwy, możemy zapisać prawo Gaussa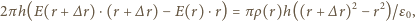
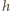 jest wysokością walca. Stąd
jest wysokością walca. Stąd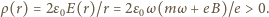
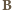 i
i 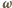 mają zwroty przeciwne, siła magnetyczna działająca na swobodny elektron ma zwrot do środka okręgu, równanie ruchu elektronu ma postać
mają zwroty przeciwne, siła magnetyczna działająca na swobodny elektron ma zwrot do środka okręgu, równanie ruchu elektronu ma postać 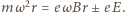 Znak
Znak 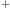 opisuje przypadek, gdy
opisuje przypadek, gdy 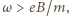 znak
znak  , gdy nierówność ma znak przeciwny. Szukana gęstość ładunku dana jest wzorem
, gdy nierówność ma znak przeciwny. Szukana gęstość ładunku dana jest wzorem 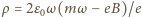 i może być dodatnia albo ujemna. Gdy
i może być dodatnia albo ujemna. Gdy 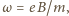 gęstość ładunku wynosi 0.
gęstość ładunku wynosi 0.
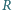 leżą jedna na drugiej na poziomej powierzchni stykając się ze ścianą. Po zakłóceniu równowagi kulka górna ślizga się wzdłuż ściany, kulka dolna ślizga się po poziomej powierzchni, a ich prędkości początkowe są zerowe. Nie ma tarcia. Znaleźć prędkość kulki dolnej po utracie kontaktu między kulkami.
leżą jedna na drugiej na poziomej powierzchni stykając się ze ścianą. Po zakłóceniu równowagi kulka górna ślizga się wzdłuż ściany, kulka dolna ślizga się po poziomej powierzchni, a ich prędkości początkowe są zerowe. Nie ma tarcia. Znaleźć prędkość kulki dolnej po utracie kontaktu między kulkami.
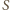 porusza się po okręgu o środku w punkcie
porusza się po okręgu o środku w punkcie 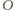 i promieniu
i promieniu 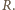 Siła dośrodkowa spełnia równanie
Siła dośrodkowa spełnia równanie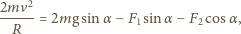
 jest prędkością środka masy,
jest prędkością środka masy, 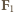 i
i 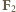 siłami reakcji ze strony podłoża i ściany,
siłami reakcji ze strony podłoża i ściany,  jest kątem, jaki tworzy wektor położenia środka masy zaczepiony w punkcie
jest kątem, jaki tworzy wektor położenia środka masy zaczepiony w punkcie 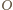 z poziomem. Oznaczając przez
z poziomem. Oznaczając przez 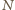 wartość siły oddziaływania między kulkami, możemy zapisać związki
wartość siły oddziaływania między kulkami, możemy zapisać związki 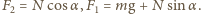 Gdy kulki przestają się stykać, w położeniu opisanym kątem
Gdy kulki przestają się stykać, w położeniu opisanym kątem 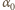 mamy
mamy 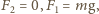
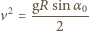
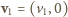 i
i 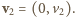 Z definicji środka masy mamy
Z definicji środka masy mamy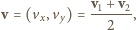
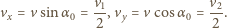
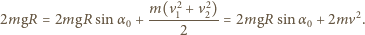
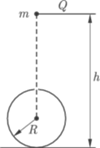
 mającego na górze niewielki otwór, wpadają z wysokości
mającego na górze niewielki otwór, wpadają z wysokości 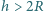 naładowane krople rtęci. Masa każdej kropli wynosi
naładowane krople rtęci. Masa każdej kropli wynosi 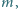 a jej ładunek elektryczny wynosi
a jej ładunek elektryczny wynosi 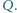 Jaki będzie kolejny numer
Jaki będzie kolejny numer 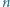 ostatniej kropli, która jeszcze wpadnie do naczynia?
ostatniej kropli, która jeszcze wpadnie do naczynia?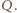 Ładunek ten rozkłada się równomiernie na powierzchni sfery i wytwarza wokół niej pole elektryczne, które jest takie jak pole pochodzące od ładunku punktowego, równego ładunkowi sfery, umieszczonego w jej środku. Na spadającą kroplę działają więc dwie siły: przyspieszająca ruch kropli siła ciężkości i opóźniająca ten ruch siła elektrostatyczna. Przyjmijmy, że do naczynia wpadło
Ładunek ten rozkłada się równomiernie na powierzchni sfery i wytwarza wokół niej pole elektryczne, które jest takie jak pole pochodzące od ładunku punktowego, równego ładunkowi sfery, umieszczonego w jej środku. Na spadającą kroplę działają więc dwie siły: przyspieszająca ruch kropli siła ciężkości i opóźniająca ten ruch siła elektrostatyczna. Przyjmijmy, że do naczynia wpadło  kropli, a więc jego ładunek wynosi
kropli, a więc jego ładunek wynosi 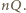 Kropla
Kropla 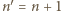 już do naczynia nie wpadnie, jeżeli jej prędkość na wysokości otworu w naczyniu będzie równa zeru.
już do naczynia nie wpadnie, jeżeli jej prędkość na wysokości otworu w naczyniu będzie równa zeru.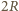 kropla spadająca z wysokości
kropla spadająca z wysokości 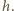 Będzie ona równa zmianie jej energii potencjalnej, na którą składa się energia pochodząca od pola grawitacyjnego i od pola elektrycznego przy spadku z wysokości
Będzie ona równa zmianie jej energii potencjalnej, na którą składa się energia pochodząca od pola grawitacyjnego i od pola elektrycznego przy spadku z wysokości 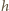 do wysokości
do wysokości 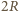 :
: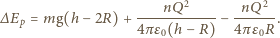
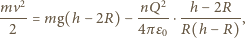
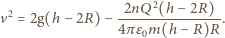
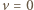 dostajemy
dostajemy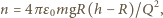
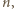 będący największą liczbą całkowitą spełniającą warunek:
będący największą liczbą całkowitą spełniającą warunek: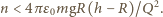
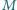 i polu powierzchni
i polu powierzchni 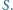 Na górnej powierzchni tłoka, bez straty energii, podskakuje
Na górnej powierzchni tłoka, bez straty energii, podskakuje 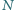 kulek, każda o masie
kulek, każda o masie 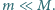 Wysokość, na jaką podskakuje każda kulka, wynosi
Wysokość, na jaką podskakuje każda kulka, wynosi 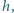 ciśnienie atmosferyczne jest równe
ciśnienie atmosferyczne jest równe 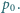 Ile wynosi ciśnienie gazu pod tłokiem?
Ile wynosi ciśnienie gazu pod tłokiem?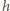 przy sprężystym zderzeniu z tłokiem przekazuje mu pęd
przy sprężystym zderzeniu z tłokiem przekazuje mu pęd 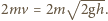 Następuje to raz w ciągu czasu
Następuje to raz w ciągu czasu 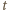 pomiędzy dwoma kolejnymi zderzeniami, który jest równy sumie czasu wznoszenia i spadania kulki:
pomiędzy dwoma kolejnymi zderzeniami, który jest równy sumie czasu wznoszenia i spadania kulki: 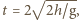 gdzie g to przyspieszenie ziemskie. Stąd znajdujemy średnią wartość siły oddziaływania jednej kulki na tłok w ciągu czasu
gdzie g to przyspieszenie ziemskie. Stąd znajdujemy średnią wartość siły oddziaływania jednej kulki na tłok w ciągu czasu 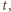 równą
równą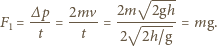
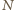 kulek na tłok znajdujemy
kulek na tłok znajdujemy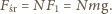
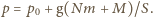
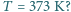 Ciepło parowania wody wynosi
Ciepło parowania wody wynosi 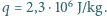
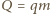 potrzebne do zamiany masy
potrzebne do zamiany masy  wody w parę podczas wrzenia zużywane jest na zwiększenie energii wewnętrznej oraz pracę przeciw siłom zewnętrznego ciśnienia:
wody w parę podczas wrzenia zużywane jest na zwiększenie energii wewnętrznej oraz pracę przeciw siłom zewnętrznego ciśnienia: 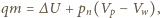 gdzie
gdzie 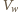 jest objętością wygotowanej wody,
jest objętością wygotowanej wody, 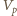 objętością powstałej pary,
objętością powstałej pary, 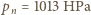 ciśnieniem pary nasyconej wody w temperaturze
ciśnieniem pary nasyconej wody w temperaturze 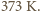 Z równania Clapeyrona
Z równania Clapeyrona 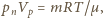 gdzie
gdzie 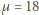 jest masą molową wody. Stosunek gęstości pary nasyconej i wody w temperaturze
jest masą molową wody. Stosunek gęstości pary nasyconej i wody w temperaturze 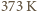 wynosi
wynosi 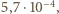 zatem objętość wygotowanej wody możemy pominąć w porównaniu z objętością powstałej pary. Stosunek zmiany energii wewnętrznej do pobranego ciepła dany jest wzorem
zatem objętość wygotowanej wody możemy pominąć w porównaniu z objętością powstałej pary. Stosunek zmiany energii wewnętrznej do pobranego ciepła dany jest wzorem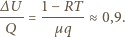
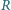 umocowany jest na poziomej płaszczyźnie. Jednorodny cienki pręt o długości
umocowany jest na poziomej płaszczyźnie. Jednorodny cienki pręt o długości 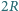 opiera się na walcu w połowie swojej długości, a jego dolny koniec
opiera się na walcu w połowie swojej długości, a jego dolny koniec 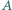 jest unieruchomiony. Po oswobodzeniu pręt ześlizguje się z walca. Nie ma tarcia. Jaka będzie prędkość górnego końca pręta
jest unieruchomiony. Po oswobodzeniu pręt ześlizguje się z walca. Nie ma tarcia. Jaka będzie prędkość górnego końca pręta 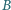 w chwili, gdy zetknie się on z powierzchnią walca?
w chwili, gdy zetknie się on z powierzchnią walca?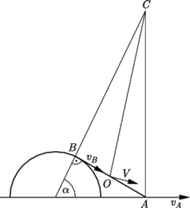
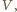 a prędkość kątową ruchu obrotowego wokół środka masy przez
a prędkość kątową ruchu obrotowego wokół środka masy przez 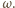 Ruch pręta możemy też traktować jako czysty obrót wokół chwilowej osi obrotu z taką samą prędkością kątową
Ruch pręta możemy też traktować jako czysty obrót wokół chwilowej osi obrotu z taką samą prędkością kątową 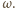 Prędkość
Prędkość 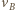 punktu
punktu 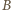 w chwili końcowej jest styczna do walca, a prędkość
w chwili końcowej jest styczna do walca, a prędkość 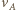 punktu
punktu 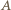 ma kierunek poziomy. Punkt
ma kierunek poziomy. Punkt 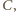 przez który przechodzi chwilowa oś obrotu, leży na przecięciu prostopadłych do prędkości
przez który przechodzi chwilowa oś obrotu, leży na przecięciu prostopadłych do prędkości 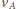 i
i 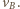 Z podobieństwa trójkątów prostokątnych na rysunku otrzymujemy, że długość odcinka
Z podobieństwa trójkątów prostokątnych na rysunku otrzymujemy, że długość odcinka 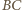 wynosi
wynosi 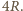 Z twierdzenia Pitagorasa długość odcinka
Z twierdzenia Pitagorasa długość odcinka 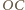 jest równa
jest równa 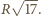 Wynika stąd, że związek między prędkością środka masy i prędkością ruchu obrotowego dany jest wzorem
Wynika stąd, że związek między prędkością środka masy i prędkością ruchu obrotowego dany jest wzorem 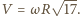 Ponieważ nie ma oporów ruchu, zachowana jest energia mechaniczna pręta
Ponieważ nie ma oporów ruchu, zachowana jest energia mechaniczna pręta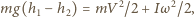
 jest masą pręta,
jest masą pręta, 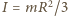 jego momentem bezwładności względem osi przechodzącej przez środek. Wysokości środka masy nad powierzchnią poziomą w chwilach początkowej i końcowej wynoszą odpowiednio
jego momentem bezwładności względem osi przechodzącej przez środek. Wysokości środka masy nad powierzchnią poziomą w chwilach początkowej i końcowej wynoszą odpowiednio 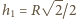 i
i 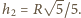 Podstawiając to do równania (1), otrzymujemy prędkość kątową
Podstawiając to do równania (1), otrzymujemy prędkość kątową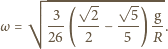
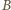 dana jest wzorem
dana jest wzorem 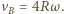
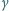 podczas ich "spadania" w polu grawitacyjnym. Oszacuj, jaką prędkość
podczas ich "spadania" w polu grawitacyjnym. Oszacuj, jaką prędkość  w górę należy nadać emiterowi promieniowania
w górę należy nadać emiterowi promieniowania 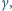 żeby skompensować zmianę energii kwantów
żeby skompensować zmianę energii kwantów 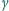 "spadających" z wysokości
"spadających" z wysokości 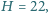 5 m (taka była różnica wysokości w oryginalnym doświadczeniu R. V. Pounda i G. A. Rebki wykonanym w roku 1960). Przyspieszenie ziemskie
5 m (taka była różnica wysokości w oryginalnym doświadczeniu R. V. Pounda i G. A. Rebki wykonanym w roku 1960). Przyspieszenie ziemskie 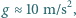 a prędkość światła
a prędkość światła 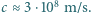
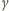 o częstości
o częstości  i energii
i energii 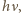 gdzie
gdzie 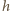 jest stałą Plancka, spadając w polu grawitacyjnym z wysokości
jest stałą Plancka, spadając w polu grawitacyjnym z wysokości 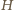 zwiększy swoja energię o
zwiększy swoja energię o 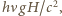 a więc jego częstość wzrośnie o
a więc jego częstość wzrośnie o 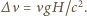 Dla niewielkich prędkości
Dla niewielkich prędkości  ruchu emitera zmiana częstości promieniowania w wyniku zjawiska Dopplera wynosi
ruchu emitera zmiana częstości promieniowania w wyniku zjawiska Dopplera wynosi 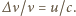 Dla skompensowania wzrostu energii kwantu
Dla skompensowania wzrostu energii kwantu 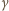 podczas spadku emiter musi oddalać się od detektora z prędkością powodującą zmniejszenie energii kwantu o wartość równą temu wzrostowi. Otrzymujemy więc:
podczas spadku emiter musi oddalać się od detektora z prędkością powodującą zmniejszenie energii kwantu o wartość równą temu wzrostowi. Otrzymujemy więc: 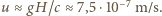 W doświadczeniu Pounda i Rebki użyto kwantów
W doświadczeniu Pounda i Rebki użyto kwantów 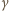 o energii
o energii 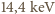 emitowanych przez izotop
emitowanych przez izotop 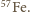
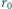 każda, powstała jedna bańka o promieniu
każda, powstała jedna bańka o promieniu 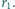 Oszacuj wartość jej promienia. Ciśnienie atmosferyczne wynosi
Oszacuj wartość jej promienia. Ciśnienie atmosferyczne wynosi 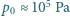 , a dla napięcia powierzchniowego
, a dla napięcia powierzchniowego 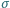 roztworu wody z mydłem przyjmij
roztworu wody z mydłem przyjmij 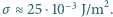
 powoduje, że w jej wnętrzu ciśnienie jest większe od zewnętrznego o
powoduje, że w jej wnętrzu ciśnienie jest większe od zewnętrznego o 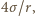 gdzie
gdzie  jest promieniem bańki. Zamknięty w bańce gaz spełnia prawo Boyle'a-Mariotte'a,
jest promieniem bańki. Zamknięty w bańce gaz spełnia prawo Boyle'a-Mariotte'a, 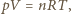 gdzie
gdzie 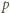 jest ciśnieniem gazu,
jest ciśnieniem gazu, 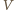 jego objętością,
jego objętością, 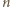 liczbą moli gazu,
liczbą moli gazu, 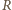 stałą gazową, a
stałą gazową, a 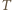 temperaturą w skali bezwzględnej. Oczywiście
temperaturą w skali bezwzględnej. Oczywiście 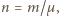 gdzie
gdzie  oznacza masę gazu, a
oznacza masę gazu, a 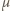 jego masę molową. Masa gazu zamkniętego w bańkach przed i po zderzeniu nie zmienia się, nie zmienia się też temperatura
jego masę molową. Masa gazu zamkniętego w bańkach przed i po zderzeniu nie zmienia się, nie zmienia się też temperatura 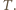 Biorąc to wszystko pod uwagę, otrzymujemy równanie spełniane przez promień
Biorąc to wszystko pod uwagę, otrzymujemy równanie spełniane przez promień 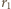 końcowej bańki:
końcowej bańki: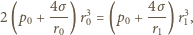
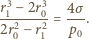
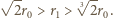
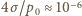 m, to
m, to 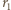 bardzo nieznacznie przewyższa
bardzo nieznacznie przewyższa 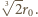
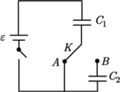
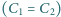 i klucza
i klucza 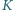 łączymy ze źródłem napięcia o sile elektromotorycznej
łączymy ze źródłem napięcia o sile elektromotorycznej  Wielokrotnie zmieniamy położenie klucza
Wielokrotnie zmieniamy położenie klucza 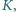 łącząc kondensator
łącząc kondensator 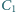 kolejno ze stykami
kolejno ze stykami 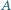 i
i 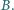 Jak zmienia się napięcie na kondensatorze
Jak zmienia się napięcie na kondensatorze 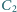 po każdym przełączeniu klucza? Rozważyć przypadki:
po każdym przełączeniu klucza? Rozważyć przypadki: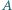 ;
;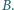
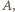 potencjał dolnej okładki kondensatora
potencjał dolnej okładki kondensatora 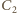 jest taki sam jak potencjał klucza. Napięcie na kondensatorze
jest taki sam jak potencjał klucza. Napięcie na kondensatorze 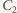 nie zmienia się i wynosi 0.
nie zmienia się i wynosi 0.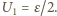 Po przełączeniu klucza do punktu
Po przełączeniu klucza do punktu 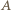 kondensator
kondensator  ładuje się do napięcia
ładuje się do napięcia 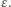 Po ponownym przełączeniu do punktu
Po ponownym przełączeniu do punktu 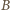 przez źródło przepływa ładunek, napięcie na obu kondensatorach maleje o tę samą wartość
przez źródło przepływa ładunek, napięcie na obu kondensatorach maleje o tę samą wartość 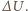 Zgodnie z prawem Kirchhoffa
Zgodnie z prawem Kirchhoffa 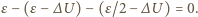 Stąd
Stąd 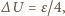 napięcie na drugim kondensatorze wynosi
napięcie na drugim kondensatorze wynosi 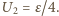 Rozumując analogicznie, otrzymujemy, że po drugim powrocie klucza do położenia
Rozumując analogicznie, otrzymujemy, że po drugim powrocie klucza do położenia 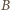 napięcie na kondensatorze
napięcie na kondensatorze 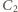 wynosi
wynosi 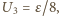 a po
a po 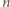 -tym powrocie
-tym powrocie 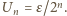 Po odpowiednio długim czasie dolny kondensator rozładuje się.
Po odpowiednio długim czasie dolny kondensator rozładuje się.
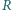 słabo uderza w ścianę i deformuje się, jak pokazano na rysunku. Deformacja
słabo uderza w ścianę i deformuje się, jak pokazano na rysunku. Deformacja 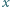 jest dużo mniejsza od promienia piłki i możemy przyjąć, że ciśnienie powietrza w piłce nie zmienia się podczas uderzenia. Zaniedbując sprężystość powłoki, oszacować czas zderzenia piłki ze ścianą. Masa piłki wynosi
jest dużo mniejsza od promienia piłki i możemy przyjąć, że ciśnienie powietrza w piłce nie zmienia się podczas uderzenia. Zaniedbując sprężystość powłoki, oszacować czas zderzenia piłki ze ścianą. Masa piłki wynosi 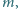 ciśnienie powietrza w piłce
ciśnienie powietrza w piłce 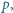 ciśnienie atmosferyczne
ciśnienie atmosferyczne 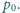

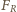 oraz siła
oraz siła 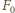 spowodowana ciśnieniem atmosferycznym. Zgodnie z trzecią zasadą dynamiki siła reakcji równa jest co do wartości sile nacisku piłki na ścianę. Ponieważ możemy zaniedbać sprężystość powłoki, więc
spowodowana ciśnieniem atmosferycznym. Zgodnie z trzecią zasadą dynamiki siła reakcji równa jest co do wartości sile nacisku piłki na ścianę. Ponieważ możemy zaniedbać sprężystość powłoki, więc 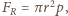 gdzie
gdzie  jest promieniem powierzchni zetknięcia piłki ze ścianą (rysunek). W celu znalezienia siły
jest promieniem powierzchni zetknięcia piłki ze ścianą (rysunek). W celu znalezienia siły 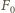 podzielmy myślowo powierzchnię piłki stykającą się z powietrzem na małe elementy o powierzchni
podzielmy myślowo powierzchnię piłki stykającą się z powietrzem na małe elementy o powierzchni 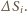 Na każdy element działa prostopadle do niego siła
Na każdy element działa prostopadle do niego siła 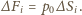 Wobec symetrii składowe równoległe do ściany wszystkich tych sił znoszą się, siła
Wobec symetrii składowe równoległe do ściany wszystkich tych sił znoszą się, siła 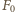 skierowana jest prostopadle w kierunku ściany i ma wartość
skierowana jest prostopadle w kierunku ściany i ma wartość 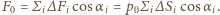 Z
Z 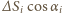 jest rzutem
jest rzutem 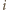 -tego elementu powierzchni na płaszczyznę pionową, a suma tych wielkości równa jest powierzchni styku piłki ze ścianą. Stąd
-tego elementu powierzchni na płaszczyznę pionową, a suma tych wielkości równa jest powierzchni styku piłki ze ścianą. Stąd 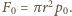 Wypadkowa siła działająca na piłkę wynosi zatem
Wypadkowa siła działająca na piłkę wynosi zatem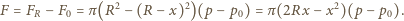
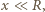 mamy
mamy 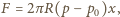 a zwrot
a zwrot 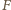 jest przeciwny do deformacji
jest przeciwny do deformacji 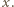 W rozważanym przybliżeniu piłka podczas zderzenia ze ścianą porusza się ruchem harmonicznym z okresem
W rozważanym przybliżeniu piłka podczas zderzenia ze ścianą porusza się ruchem harmonicznym z okresem 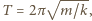 gdzie
gdzie 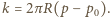 Czas zderzenia piłki ze ścianą równy jest połowie okresu:
Czas zderzenia piłki ze ścianą równy jest połowie okresu: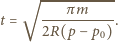
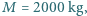 promieniu wirnika
promieniu wirnika 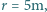 w powietrzu o gęstości
w powietrzu o gęstości 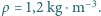 Dla uproszczenia założyć, że wirnik tworzy skierowaną pionowo w dół strugę powietrza o jednorodnym rozkładzie prędkości i o przekroju koła o promieniu
Dla uproszczenia założyć, że wirnik tworzy skierowaną pionowo w dół strugę powietrza o jednorodnym rozkładzie prędkości i o przekroju koła o promieniu 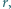 oraz pominąć mały wirnik w ogonie.
oraz pominąć mały wirnik w ogonie.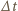 przez przekrój wirnika przechodzi strumień
przez przekrój wirnika przechodzi strumień 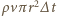 powietrza. Wirnik przekazuje więc mu pęd
powietrza. Wirnik przekazuje więc mu pęd  w jednostce czasu, więc siła nośna wynosi
w jednostce czasu, więc siła nośna wynosi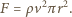
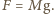 Z kolei energia kinetyczna powietrza popychanego w jednostce czasu wynosi
Z kolei energia kinetyczna powietrza popychanego w jednostce czasu wynosi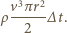
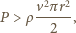
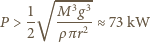
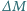 jest wyrzucana w czasie
jest wyrzucana w czasie 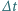 do tyłu ze stałą prędkością
do tyłu ze stałą prędkością  względem rakiety. Pokazać, że przyspieszenie rakiety rośnie wraz z ubytkiem paliwa. Czy tak samo rośnie moc silnika
względem rakiety. Pokazać, że przyspieszenie rakiety rośnie wraz z ubytkiem paliwa. Czy tak samo rośnie moc silnika 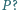
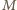 oznacza chwilową masę rakiety, a
oznacza chwilową masę rakiety, a 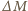 masę wyrzucaną w krótkim czasie
masę wyrzucaną w krótkim czasie 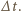 Pęd rakiety zmienia się w tym czasie o
Pęd rakiety zmienia się w tym czasie o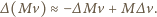
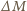 gazów o prędkości
gazów o prędkości  Z zasady zachowania pędu musi więc zajść
Z zasady zachowania pędu musi więc zajść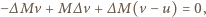
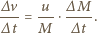
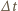 to
to