Liczbę całkowitą dodatnią 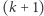-cyfrową możemy zapisać w postaci

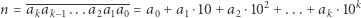(kreska nad wyrażeniem informuje, iż nie jest to po prostu mnożenie). Liczbę 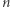możemy oszacować, znając jej pierwszą cyfrę oraz liczbę cyfr. Zachodzą oczywiste nierówności:

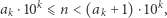z których warto skorzystać w zadaniach 1, 3, 9 i 10.

Przez 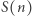oznaczać będziemy sumę cyfr liczby 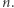Zauważmy, że liczba

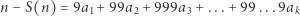dzieli się przez 9, zatem suma cyfr liczby naturalnej daje taką samą resztę z dzielenia przez 9, co ta liczba. Tego faktu używamy w zadaniach 1, 2, 4, 5 i 9.

Dzięki algorytmowi pisemnego dodawania mamy nierówność

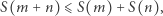która jest pomocna w zadaniach 6, 7 i 8.

Na koniec przypomnimy o pewnej własności dzielenia z resztą, która jest w poniższych zadaniach pomocna: iloczyn liczb całkowitych daje taką samą resztę z dzielenia przez 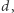co iloczyn ich reszt z dzielenia przez 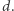Dowód pozostawiamy Czytelnikowi.

Zadania. W każdym zadaniu 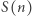oznacza sumę cyfr liczby