Kącik początkującego olimpijczyka

Symetria w algebrze

O wyrażeniach symetrycznych oraz uproszczeniach, które można stosować w rozwiązywaniu zadań z takimi wyrażeniami.

Niech 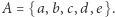$|A$ Rozważmy funkcję 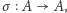$σ A$ określoną następująco:

σ (a) = d, σ(b) = c, σ(c) = e, σ(d) = a, σ (e) = b.

Zwróćmy uwagę, że wśród wartości funkcji 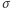$| σ$ każdy element zbioru 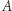$|A$ występuje dokładnie raz. Odwzorowania o tej własności będziemy nazywać permutacjami zmiennych. Działają one w naturalny sposób na wyrażeniach algebraicznych, na przykład opisana wyżej 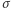$σ$ robi to tak:

a2b+ b2c+ c2d + d2e + e2a z d2c + c2e + e2a+ a2b + b2d.

Wyrażenia algebraiczne otrzymane z danego poprzez permutacje zmiennych będziemy nazywać jego symetrycznymi wersjami. Jeśli wszystkie symetryczne wersje są równe, to wyrażenie nazywamy symetrycznym. Dla jasności, wyrażenie 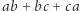$ab + bc +ca$ jest symetryczne, a wyrażenie 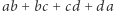$|ab+ bc + cd + da$ nie jest. Pojęcie symetryczności można intuicyjnie rozszerzyć: równanie jest symetryczne, jeśli każda jego symetryczna wersja jest mu równoważna, podobnie nierówność, układ równań itp.

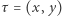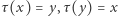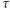Przez zapis $| τ = (x,y)$ rozumiemy, że $| τ(x) = y,τ (y) = x$ oraz $| τ$ jest identycznością na wszystkich pozostałych zmiennych. Taką permutację nazywamy transpozycją. Aby sprawdzić symetryczność, można ograniczyć się do transpozycji jednej zmiennej ze wszystkimi pozostałymi, czyli przykładowo dla wyrażenia 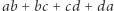$| ab + bc+ cd + da$ byłyby to 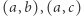$| (a,b),(a,c)$ i $| (a,d).$

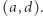
Jeśli z symetrycznego równania lub układu równań wywnioskujemy jakąkolwiek własność jego niewiadomych, to spełnione są także własności do niej symetryczne, które można udowodnić w pełni analogicznie. Takie rozumowanie stosujemy w zadaniach 1, 3, 5 i 9.

Wraz z każdym rozwiązaniem symetryczne równanie lub układ ma rozwiązania powstałe przez jego permutacje. Pojawia się to w zadaniach 2, 3 i 7.

Wobec powyższego w zadaniach z algebraiczną symetrią możemy na początku rozwiązania narzucić pewien porządek wśród niewiadomych, gdyż rozwiązania nieuporządkowane dostaniemy poprzez permutacje uporządkowanych. Zabieg ten można prześledzić w zadaniach 4, 6, 7, 8 i 10.