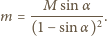Klub 44F - zadania III 2018»Zadanie 655
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania III 2018
- Publikacja w Delcie: marzec 2018
- Publikacja elektroniczna: 28 lutego 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (106 KB)
Ciężarek o masie  wisi na nici. Na jaką najmniejszą wysokość należy podnieść ciężarek, aby spadając, rozerwał nić? Minimalna siła wystarczająca do rozerwania nici wynosi
wisi na nici. Na jaką najmniejszą wysokość należy podnieść ciężarek, aby spadając, rozerwał nić? Minimalna siła wystarczająca do rozerwania nici wynosi 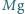 (
( 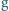 jest przyspieszeniem ziemskim) i przed rozerwaniem wydłuża ją o
jest przyspieszeniem ziemskim) i przed rozerwaniem wydłuża ją o  Zakładamy, że siła naprężenia nici jest proporcjonalna do jej wydłużenia aż do zerwania.
Zakładamy, że siła naprężenia nici jest proporcjonalna do jej wydłużenia aż do zerwania.
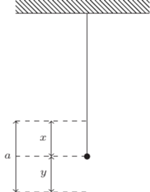
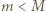 . Oznaczmy przez
. Oznaczmy przez 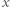 wydłużenie nici w stanie równowagi, mamy wtedy związki:
wydłużenie nici w stanie równowagi, mamy wtedy związki: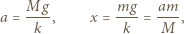
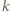 jest współczynnikiem sprężystości nici. Dodatkowe wydłużenie w momencie rozerwania nici wynosi
jest współczynnikiem sprężystości nici. Dodatkowe wydłużenie w momencie rozerwania nici wynosi 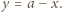
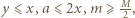 na ciężarek cały czas działa siła sprężystości i aż do momentu zerwania nici porusza się on ruchem harmonicznym. Najmniejsza wysokość, na jaką musimy go podnieść, wynosi
na ciężarek cały czas działa siła sprężystości i aż do momentu zerwania nici porusza się on ruchem harmonicznym. Najmniejsza wysokość, na jaką musimy go podnieść, wynosi 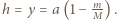
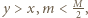 możemy skorzystać z zasady zachowania energii:
możemy skorzystać z zasady zachowania energii: 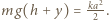
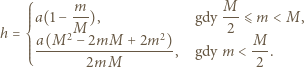
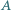 porusza się z prędkością
porusza się z prędkością 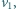 goni go pojazd
goni go pojazd 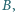 poruszający się w tym samym kierunku z prędkością
poruszający się w tym samym kierunku z prędkością 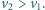 W chwili początkowej odległość między pojazdami wynosi
W chwili początkowej odległość między pojazdami wynosi 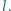 Po jakim czasie pojazd
Po jakim czasie pojazd 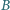 dogoni
dogoni  z punktu widzenia obserwatora na Ziemi oraz z punktu widzenia kosmonauty w pojeździe
z punktu widzenia obserwatora na Ziemi oraz z punktu widzenia kosmonauty w pojeździe 
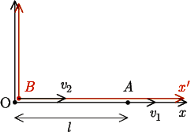
 zsynchronizowali swoje zegary, gdy znajdowali się w tym samym miejscu i tę chwilę uznali za zerową. Zdarzeniem początkowym jest odbicie sygnału radarowego wysłanego z Ziemi od pojazdu
zsynchronizowali swoje zegary, gdy znajdowali się w tym samym miejscu i tę chwilę uznali za zerową. Zdarzeniem początkowym jest odbicie sygnału radarowego wysłanego z Ziemi od pojazdu 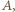 któremu obserwator O przypisuje współrzędną czasową
któremu obserwator O przypisuje współrzędną czasową 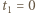 oraz współrzędną przestrzenną
oraz współrzędną przestrzenną 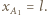 W układzie statku
W układzie statku 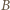 to samo zdarzenie zachodzi w chwili
to samo zdarzenie zachodzi w chwili 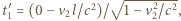 w miejscu o współrzędnej przestrzennej
w miejscu o współrzędnej przestrzennej 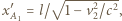 zgodnie z transformacją Lorentza.
zgodnie z transformacją Lorentza.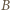 dogania
dogania 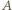 - zachodzi w układzie Ziemi w miejscu o współrzędnej
- zachodzi w układzie Ziemi w miejscu o współrzędnej 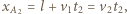 stąd chwila zdarzenia wynosi
stąd chwila zdarzenia wynosi 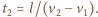 W układzie statku
W układzie statku 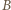 miejsce zdarzenia ma współrzędną
miejsce zdarzenia ma współrzędną 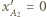 i zachodzi w chwili
i zachodzi w chwili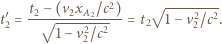
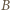 dogoni
dogoni 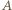 po czasie
po czasie 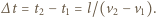
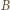 szukany czas wynosi
szukany czas wynosi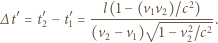
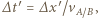 gdzie
gdzie 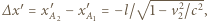 a
a 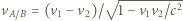 jest prędkością statku
jest prędkością statku 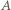 względem
względem 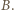

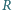 leżą jedna na drugiej na poziomej powierzchni stykając się ze ścianą. Po zakłóceniu równowagi kulka górna ślizga się wzdłuż ściany, kulka dolna ślizga się po poziomej powierzchni, a ich prędkości początkowe są zerowe. Nie ma tarcia. Znaleźć prędkość kulki dolnej po utracie kontaktu między kulkami.
leżą jedna na drugiej na poziomej powierzchni stykając się ze ścianą. Po zakłóceniu równowagi kulka górna ślizga się wzdłuż ściany, kulka dolna ślizga się po poziomej powierzchni, a ich prędkości początkowe są zerowe. Nie ma tarcia. Znaleźć prędkość kulki dolnej po utracie kontaktu między kulkami.
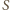 porusza się po okręgu o środku w punkcie
porusza się po okręgu o środku w punkcie 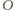 i promieniu
i promieniu 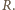 Siła dośrodkowa spełnia równanie
Siła dośrodkowa spełnia równanie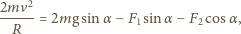
 jest prędkością środka masy,
jest prędkością środka masy, 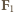 i
i 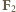 siłami reakcji ze strony podłoża i ściany,
siłami reakcji ze strony podłoża i ściany,  jest kątem, jaki tworzy wektor położenia środka masy zaczepiony w punkcie
jest kątem, jaki tworzy wektor położenia środka masy zaczepiony w punkcie 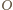 z poziomem. Oznaczając przez
z poziomem. Oznaczając przez 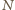 wartość siły oddziaływania między kulkami, możemy zapisać związki
wartość siły oddziaływania między kulkami, możemy zapisać związki 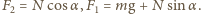 Gdy kulki przestają się stykać, w położeniu opisanym kątem
Gdy kulki przestają się stykać, w położeniu opisanym kątem 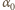 mamy
mamy 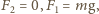
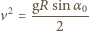
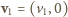 i
i 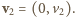 Z definicji środka masy mamy
Z definicji środka masy mamy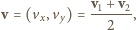
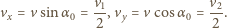
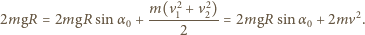
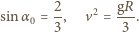
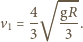
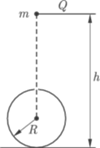
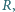 mającego na górze niewielki otwór, wpadają z wysokości
mającego na górze niewielki otwór, wpadają z wysokości 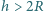 naładowane krople rtęci. Masa każdej kropli wynosi
naładowane krople rtęci. Masa każdej kropli wynosi 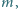 a jej ładunek elektryczny wynosi
a jej ładunek elektryczny wynosi 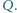 Jaki będzie kolejny numer
Jaki będzie kolejny numer 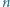 ostatniej kropli, która jeszcze wpadnie do naczynia?
ostatniej kropli, która jeszcze wpadnie do naczynia?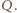 Ładunek ten rozkłada się równomiernie na powierzchni sfery i wytwarza wokół niej pole elektryczne, które jest takie jak pole pochodzące od ładunku punktowego, równego ładunkowi sfery, umieszczonego w jej środku. Na spadającą kroplę działają więc dwie siły: przyspieszająca ruch kropli siła ciężkości i opóźniająca ten ruch siła elektrostatyczna. Przyjmijmy, że do naczynia wpadło
Ładunek ten rozkłada się równomiernie na powierzchni sfery i wytwarza wokół niej pole elektryczne, które jest takie jak pole pochodzące od ładunku punktowego, równego ładunkowi sfery, umieszczonego w jej środku. Na spadającą kroplę działają więc dwie siły: przyspieszająca ruch kropli siła ciężkości i opóźniająca ten ruch siła elektrostatyczna. Przyjmijmy, że do naczynia wpadło  kropli, a więc jego ładunek wynosi
kropli, a więc jego ładunek wynosi 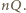 Kropla
Kropla 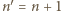 już do naczynia nie wpadnie, jeżeli jej prędkość na wysokości otworu w naczyniu będzie równa zeru.
już do naczynia nie wpadnie, jeżeli jej prędkość na wysokości otworu w naczyniu będzie równa zeru.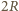 kropla spadająca z wysokości
kropla spadająca z wysokości 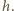 Będzie ona równa zmianie jej energii potencjalnej, na którą składa się energia pochodząca od pola grawitacyjnego i od pola elektrycznego przy spadku z wysokości
Będzie ona równa zmianie jej energii potencjalnej, na którą składa się energia pochodząca od pola grawitacyjnego i od pola elektrycznego przy spadku z wysokości 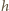 do wysokości
do wysokości 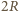 :
: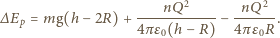
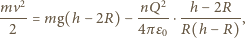
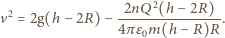
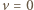 dostajemy
dostajemy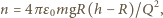
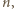 będący największą liczbą całkowitą spełniającą warunek:
będący największą liczbą całkowitą spełniającą warunek: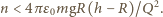
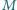 i polu powierzchni
i polu powierzchni 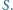 Na górnej powierzchni tłoka, bez straty energii, podskakuje
Na górnej powierzchni tłoka, bez straty energii, podskakuje 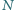 kulek, każda o masie
kulek, każda o masie 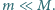 Wysokość, na jaką podskakuje każda kulka, wynosi
Wysokość, na jaką podskakuje każda kulka, wynosi 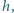 ciśnienie atmosferyczne jest równe
ciśnienie atmosferyczne jest równe 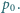 Ile wynosi ciśnienie gazu pod tłokiem?
Ile wynosi ciśnienie gazu pod tłokiem?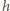 przy sprężystym zderzeniu z tłokiem przekazuje mu pęd
przy sprężystym zderzeniu z tłokiem przekazuje mu pęd 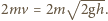 Następuje to raz w ciągu czasu
Następuje to raz w ciągu czasu 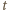 pomiędzy dwoma kolejnymi zderzeniami, który jest równy sumie czasu wznoszenia i spadania kulki:
pomiędzy dwoma kolejnymi zderzeniami, który jest równy sumie czasu wznoszenia i spadania kulki: 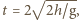 gdzie g to przyspieszenie ziemskie. Stąd znajdujemy średnią wartość siły oddziaływania jednej kulki na tłok w ciągu czasu
gdzie g to przyspieszenie ziemskie. Stąd znajdujemy średnią wartość siły oddziaływania jednej kulki na tłok w ciągu czasu 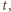 równą
równą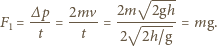
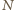 kulek na tłok znajdujemy
kulek na tłok znajdujemy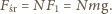
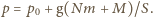
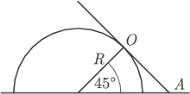
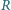 umocowany jest na poziomej płaszczyźnie. Jednorodny cienki pręt o długości
umocowany jest na poziomej płaszczyźnie. Jednorodny cienki pręt o długości 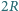 opiera się na walcu w połowie swojej długości, a jego dolny koniec
opiera się na walcu w połowie swojej długości, a jego dolny koniec 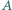 jest unieruchomiony. Po oswobodzeniu pręt ześlizguje się z walca. Nie ma tarcia. Jaka będzie prędkość górnego końca pręta
jest unieruchomiony. Po oswobodzeniu pręt ześlizguje się z walca. Nie ma tarcia. Jaka będzie prędkość górnego końca pręta 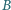 w chwili, gdy zetknie się on z powierzchnią walca?
w chwili, gdy zetknie się on z powierzchnią walca?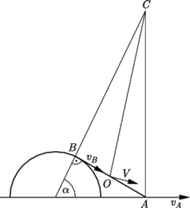
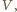 a prędkość kątową ruchu obrotowego wokół środka masy przez
a prędkość kątową ruchu obrotowego wokół środka masy przez 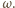 Ruch pręta możemy też traktować jako czysty obrót wokół chwilowej osi obrotu z taką samą prędkością kątową
Ruch pręta możemy też traktować jako czysty obrót wokół chwilowej osi obrotu z taką samą prędkością kątową 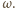 Prędkość
Prędkość 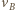 punktu
punktu 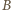 w chwili końcowej jest styczna do walca, a prędkość
w chwili końcowej jest styczna do walca, a prędkość 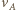 punktu
punktu 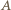 ma kierunek poziomy. Punkt
ma kierunek poziomy. Punkt 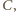 przez który przechodzi chwilowa oś obrotu, leży na przecięciu prostopadłych do prędkości
przez który przechodzi chwilowa oś obrotu, leży na przecięciu prostopadłych do prędkości 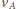 i
i 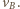 Z podobieństwa trójkątów prostokątnych na rysunku otrzymujemy, że długość odcinka
Z podobieństwa trójkątów prostokątnych na rysunku otrzymujemy, że długość odcinka 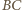 wynosi
wynosi 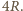 Z twierdzenia Pitagorasa długość odcinka
Z twierdzenia Pitagorasa długość odcinka 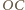 jest równa
jest równa 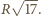 Wynika stąd, że związek między prędkością środka masy i prędkością ruchu obrotowego dany jest wzorem
Wynika stąd, że związek między prędkością środka masy i prędkością ruchu obrotowego dany jest wzorem 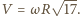 Ponieważ nie ma oporów ruchu, zachowana jest energia mechaniczna pręta
Ponieważ nie ma oporów ruchu, zachowana jest energia mechaniczna pręta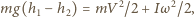
 jest masą pręta,
jest masą pręta, 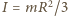 jego momentem bezwładności względem osi przechodzącej przez środek. Wysokości środka masy nad powierzchnią poziomą w chwilach początkowej i końcowej wynoszą odpowiednio
jego momentem bezwładności względem osi przechodzącej przez środek. Wysokości środka masy nad powierzchnią poziomą w chwilach początkowej i końcowej wynoszą odpowiednio 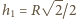 i
i 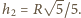 Podstawiając to do równania (1), otrzymujemy prędkość kątową
Podstawiając to do równania (1), otrzymujemy prędkość kątową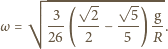
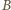 dana jest wzorem
dana jest wzorem 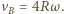
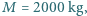 promieniu wirnika
promieniu wirnika 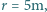 w powietrzu o gęstości
w powietrzu o gęstości 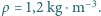 Dla uproszczenia założyć, że wirnik tworzy skierowaną pionowo w dół strugę powietrza o jednorodnym rozkładzie prędkości i o przekroju koła o promieniu
Dla uproszczenia założyć, że wirnik tworzy skierowaną pionowo w dół strugę powietrza o jednorodnym rozkładzie prędkości i o przekroju koła o promieniu 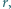 oraz pominąć mały wirnik w ogonie.
oraz pominąć mały wirnik w ogonie.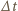 przez przekrój wirnika przechodzi strumień
przez przekrój wirnika przechodzi strumień 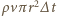 powietrza. Wirnik przekazuje więc mu pęd
powietrza. Wirnik przekazuje więc mu pęd  w jednostce czasu, więc siła nośna wynosi
w jednostce czasu, więc siła nośna wynosi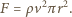
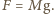 Z kolei energia kinetyczna powietrza popychanego w jednostce czasu wynosi
Z kolei energia kinetyczna powietrza popychanego w jednostce czasu wynosi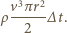
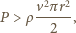
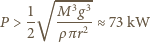
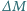 jest wyrzucana w czasie
jest wyrzucana w czasie 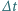 do tyłu ze stałą prędkością
do tyłu ze stałą prędkością  względem rakiety. Pokazać, że przyspieszenie rakiety rośnie wraz z ubytkiem paliwa. Czy tak samo rośnie moc silnika
względem rakiety. Pokazać, że przyspieszenie rakiety rośnie wraz z ubytkiem paliwa. Czy tak samo rośnie moc silnika 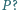
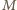 oznacza chwilową masę rakiety, a
oznacza chwilową masę rakiety, a 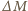 masę wyrzucaną w krótkim czasie
masę wyrzucaną w krótkim czasie 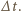 Pęd rakiety zmienia się w tym czasie o
Pęd rakiety zmienia się w tym czasie o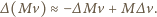
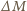 gazów o prędkości
gazów o prędkości  Z zasady zachowania pędu musi więc zajść
Z zasady zachowania pędu musi więc zajść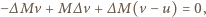
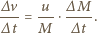
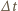 to
to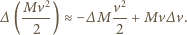
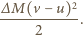
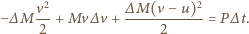
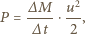
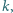 masę
masę 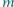 i długość
i długość 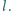 Okrąg zrobiony z tego kabla obraca się z prędkością kątową
Okrąg zrobiony z tego kabla obraca się z prędkością kątową 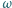 w płaszczyźnie poziomej wokół osi pionowej, przechodzącej przez środek okręgu. Wyznaczyć promień obracającego się pierścienia.
w płaszczyźnie poziomej wokół osi pionowej, przechodzącej przez środek okręgu. Wyznaczyć promień obracającego się pierścienia.
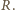 Rozważmy mały element tego okręgu o długości
Rozważmy mały element tego okręgu o długości 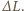 Jego masa to
Jego masa to 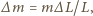 gdzie
gdzie 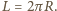 Na wydzielony element na jego końcach działają dwie siły naprężenia
Na wydzielony element na jego końcach działają dwie siły naprężenia 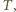 skierowane stycznie do okręgu. Ich wypadkowa
skierowane stycznie do okręgu. Ich wypadkowa 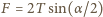 nadaje rozważanemu elementowi przyspieszenie dośrodkowe
nadaje rozważanemu elementowi przyspieszenie dośrodkowe 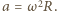 Równanie ruchu tego elementu ma postać
Równanie ruchu tego elementu ma postać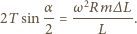
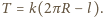 Uwzględniając, że kąt
Uwzględniając, że kąt 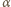 jest mały, czyli
jest mały, czyli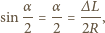
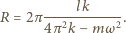

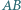 o masie
o masie 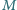 przyczepione jest wahadło matematyczne
przyczepione jest wahadło matematyczne 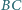 o masie
o masie  Punkt zawieszenia
Punkt zawieszenia 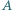 tego wahadła podwójnego drga harmonicznie wzdłuż linii poziomej z częstością
tego wahadła podwójnego drga harmonicznie wzdłuż linii poziomej z częstością 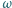 i małą amplitudą. Znaleźć długość nici dolnego wahadła, jeżeli górna nić przez cały czas pozostaje pionowa.
i małą amplitudą. Znaleźć długość nici dolnego wahadła, jeżeli górna nić przez cały czas pozostaje pionowa.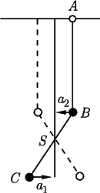
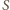 układu nie przemieszcza się w kierunku poziomym, a kulki w każdej chwili poruszają się w kierunkach przeciwnych. Stosunek ich przyspieszeń w kierunku poziomym wynosi
układu nie przemieszcza się w kierunku poziomym, a kulki w każdej chwili poruszają się w kierunkach przeciwnych. Stosunek ich przyspieszeń w kierunku poziomym wynosi 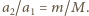 Oznaczmy szukaną długość dolnej nici przez
Oznaczmy szukaną długość dolnej nici przez 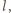 a odległość dolnej kulki od środka masy przez
a odległość dolnej kulki od środka masy przez 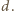 Z rysunku widać, że
Z rysunku widać, że 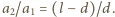 Z porównania wzorów na stosunki przyspieszeń otrzymujemy
Z porównania wzorów na stosunki przyspieszeń otrzymujemy 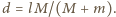 Ponieważ amplituda drgań punktu
Ponieważ amplituda drgań punktu 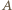 jest mała, przemieszczenia środka masy układu w kierunku pionowym również są małe i dolna kulka zachowuje się w przybliżeniu jak wahadło matematyczne o długości
jest mała, przemieszczenia środka masy układu w kierunku pionowym również są małe i dolna kulka zachowuje się w przybliżeniu jak wahadło matematyczne o długości 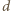 zawieszone w nieruchomym punkcie
zawieszone w nieruchomym punkcie 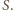 Częstość drgań tego wahadła jest taka sama jak częstość drgań punktu
Częstość drgań tego wahadła jest taka sama jak częstość drgań punktu 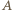 i wynosi
i wynosi 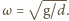 Stąd dolna nić ma długość
Stąd dolna nić ma długość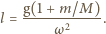
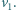 Lisa goni pies, którego prędkość ma stałą wartość
Lisa goni pies, którego prędkość ma stałą wartość 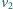 i skierowana jest cały czas na lisa. W chwili, gdy prędkości
i skierowana jest cały czas na lisa. W chwili, gdy prędkości 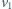 i
i 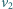 są do siebie prostopadłe, odległość między lisem a psem wynosi
są do siebie prostopadłe, odległość między lisem a psem wynosi 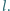 Jakie jest w tym momencie przyspieszenie psa?
Jakie jest w tym momencie przyspieszenie psa?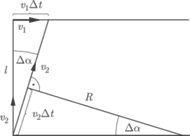
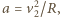 gdzie
gdzie 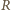 jest promieniem krzywizny toru w danym miejscu. W bardzo krótkim czasie
jest promieniem krzywizny toru w danym miejscu. W bardzo krótkim czasie 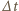 wektor prędkości psa obraca się o kąt
wektor prędkości psa obraca się o kąt 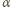 dany wzorem
dany wzorem 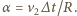 W tym samym czasie lis przebywa drogę
W tym samym czasie lis przebywa drogę 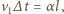 gdyż wektor prędkości psa skierowany jest cały czas na lisa. Stąd
gdyż wektor prędkości psa skierowany jest cały czas na lisa. Stąd 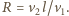 Szukana wartość przyspieszenia wynosi
Szukana wartość przyspieszenia wynosi 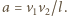
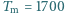 K, promień Słońca
K, promień Słońca 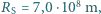 temperatura powierzchni Słońca
temperatura powierzchni Słońca 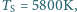 a stała Boltzmanna
a stała Boltzmanna 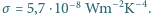
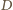 od jego środka wynosi:
od jego środka wynosi: 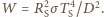 Dla uproszczenia dalszych obliczeń przyjmijmy, że możemy pominąć kątowe rozmiary Słońca. Wówczas ciało o promieniu
Dla uproszczenia dalszych obliczeń przyjmijmy, że możemy pominąć kątowe rozmiary Słońca. Wówczas ciało o promieniu  absorbuje moc
absorbuje moc 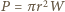 i, po osiągnięciu temperatury równowagi
i, po osiągnięciu temperatury równowagi 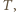 tę samą moc emituje. Mamy więc
tę samą moc emituje. Mamy więc 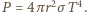 Meteoroid pozostaje w stanie stałym, gdy
Meteoroid pozostaje w stanie stałym, gdy 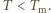 Oznacza to, że odległość od Słońca stałych meteoroidów żelaznych musi spełniać warunek:
Oznacza to, że odległość od Słońca stałych meteoroidów żelaznych musi spełniać warunek: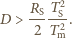
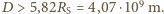 Nasze oszacowanie jest zaniżone, gdyż w tak małej odległości od Słońca poprawka wynikająca z faktu, że jest ono źródłem rozciągłym jest już dość znaczna - rozmiary kątowe Słońca "widziane" przez meteoroid wynoszą bowiem wówczas około
Nasze oszacowanie jest zaniżone, gdyż w tak małej odległości od Słońca poprawka wynikająca z faktu, że jest ono źródłem rozciągłym jest już dość znaczna - rozmiary kątowe Słońca "widziane" przez meteoroid wynoszą bowiem wówczas około 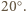
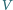 względem Ziemi takie odłamki mogą wchodzić do jej atmosfery. Przyjmij, że masa Słońca
względem Ziemi takie odłamki mogą wchodzić do jej atmosfery. Przyjmij, że masa Słońca 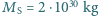 , odległość Ziemia-Słońce
, odległość Ziemia-Słońce 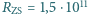 m, a stała grawitacji
m, a stała grawitacji 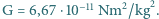
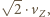 gdzie
gdzie 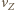 to prędkość, z jaką Ziemia obiega Słońce (
to prędkość, z jaką Ziemia obiega Słońce ( 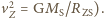 Maksymalna prędkość meteoroid-Ziemia wynosi więc
Maksymalna prędkość meteoroid-Ziemia wynosi więc 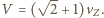 Po podstawieniu wartości liczbowych otrzymujemy
Po podstawieniu wartości liczbowych otrzymujemy 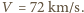
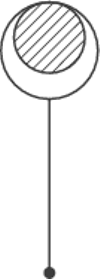
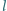 przyczepiono małą kulkę o masie
przyczepiono małą kulkę o masie 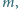 a do górnego końca rurkę w kształcie walca o wewnętrznym promieniu
a do górnego końca rurkę w kształcie walca o wewnętrznym promieniu 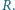 Masy pręta i rurki są zaniedbywalne. Rurka nasunięta jest luźno na nieruchomą, poziomą oś. Współczynnik tarcia między wewnętrzną powierzchnią rurki i osią jest równy
Masy pręta i rurki są zaniedbywalne. Rurka nasunięta jest luźno na nieruchomą, poziomą oś. Współczynnik tarcia między wewnętrzną powierzchnią rurki i osią jest równy 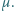 Dla jakich wartości kąta
Dla jakich wartości kąta 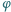 odchylenia pręta od pionu tak skonstruowane wahadło może znajdować się w równowadze?
odchylenia pręta od pionu tak skonstruowane wahadło może znajdować się w równowadze?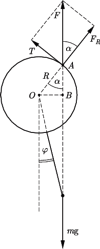
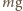 zaczepiona w środku kulki oraz siły reakcji
zaczepiona w środku kulki oraz siły reakcji 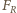 i tarcia
i tarcia 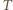 w punkcie
w punkcie 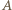 styczności osi z wewnętrzną powierzchnią rurki. Suma momentów tych sił względem dowolnego punktu wynosi zero, zatem proste, wzdłuż których działają siły, muszą się przecinać w jednym punkcie. Wynika stąd, że punkt
styczności osi z wewnętrzną powierzchnią rurki. Suma momentów tych sił względem dowolnego punktu wynosi zero, zatem proste, wzdłuż których działają siły, muszą się przecinać w jednym punkcie. Wynika stąd, że punkt 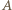 leży na przecięciu prostej pionowej, przechodzącej przez środek masy kulki z wewnętrzną powierzchnią rurki. Gdy środek kulki przemieszczony jest w prawo lub w lewo na odległość większą niż promień
leży na przecięciu prostej pionowej, przechodzącej przez środek masy kulki z wewnętrzną powierzchnią rurki. Gdy środek kulki przemieszczony jest w prawo lub w lewo na odległość większą niż promień 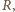 równowaga jest niemożliwa. Gdy kąt
równowaga jest niemożliwa. Gdy kąt 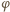 odchylenia wahadła od pionu jest maksymalny, tarcie statyczne osiąga największą możliwą wartość
odchylenia wahadła od pionu jest maksymalny, tarcie statyczne osiąga największą możliwą wartość 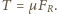 Ponieważ w stanie równowagi wypadkowa
Ponieważ w stanie równowagi wypadkowa 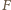 sił tarcia i reakcji skierowana jest pionowo w górę, zachodzi związek
sił tarcia i reakcji skierowana jest pionowo w górę, zachodzi związek 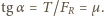 Odcinek
Odcinek 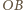 na rysunku możemy wyrazić przez kąty
na rysunku możemy wyrazić przez kąty 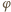 i
i 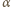 wzorem
wzorem 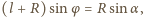 stąd
stąd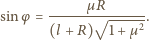
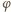 nie zależy od masy kulki. Dla
nie zależy od masy kulki. Dla 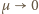 stan równowagi możliwy jest tylko dla pionowego położenia wahadła. Gdy
stan równowagi możliwy jest tylko dla pionowego położenia wahadła. Gdy 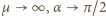 i
i 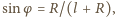 wtedy maksymalne odchylenie kulki w prawo dąży do
wtedy maksymalne odchylenie kulki w prawo dąży do 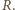 Gdy występuje tarcie w osi, wahadło może znaleźć się w równowadze także w położeniu odwróconym, kiedy kulka znajduje się powyżej osi.
Gdy występuje tarcie w osi, wahadło może znaleźć się w równowadze także w położeniu odwróconym, kiedy kulka znajduje się powyżej osi. każdy. Osie walców są równoległe, promienie są równe
każdy. Osie walców są równoległe, promienie są równe 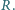 Na początku jeden z walców spoczywa, a drugi toczy się bez poślizgu w kierunku pierwszego z prędkością ruchu postępowego
Na początku jeden z walców spoczywa, a drugi toczy się bez poślizgu w kierunku pierwszego z prędkością ruchu postępowego 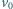 aż do centralnego, sprężystego zderzenia. Współczynnik tarcia kinetycznego walców o podłoże jest równy
aż do centralnego, sprężystego zderzenia. Współczynnik tarcia kinetycznego walców o podłoże jest równy 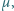 tarcie między walcami jest zaniedbywalne. Znaleźć maksymalną odległość między walcami po zderzeniu.
tarcie między walcami jest zaniedbywalne. Znaleźć maksymalną odległość między walcami po zderzeniu.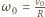 nie zmienia się w wyniku zderzenia. Z zasad zachowania pędu i energii (zderzenie sprężyste) wynika, że po zderzeniu prędkość ruchu postępowego pierwszego walca wynosi zero, a drugiego
nie zmienia się w wyniku zderzenia. Z zasad zachowania pędu i energii (zderzenie sprężyste) wynika, że po zderzeniu prędkość ruchu postępowego pierwszego walca wynosi zero, a drugiego 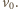 Po zderzeniu na pierwszy walec działa siła tarcia skierowana do przodu. Jego prędkość ruchu postępowego rośnie liniowo z czasem:
Po zderzeniu na pierwszy walec działa siła tarcia skierowana do przodu. Jego prędkość ruchu postępowego rośnie liniowo z czasem: 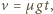 prędkość kątowa ruchu obrotowego maleje liniowo z czasem:
prędkość kątowa ruchu obrotowego maleje liniowo z czasem: 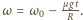 Po czasie
Po czasie 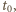 gdy spełniony jest związek
gdy spełniony jest związek 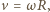 rozpoczyna się toczenie bez poślizgu. Stąd
rozpoczyna się toczenie bez poślizgu. Stąd 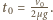 Na drugi walec działa siła tarcia skierowana do tyłu. Jego prędkość ruchu postępowego maleje liniowo z czasem, prędkość ruchu obrotowego rośnie liniowo z czasem. Po czasie
Na drugi walec działa siła tarcia skierowana do tyłu. Jego prędkość ruchu postępowego maleje liniowo z czasem, prędkość ruchu obrotowego rośnie liniowo z czasem. Po czasie 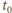 drugi walec również zaczyna toczyć się bez poślizgu. Od chwili
drugi walec również zaczyna toczyć się bez poślizgu. Od chwili 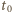 prędkości ruchu postępowego obu walców wynoszą
prędkości ruchu postępowego obu walców wynoszą 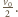 Drogi przebyte przez walce w czasie
Drogi przebyte przez walce w czasie 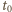 wynoszą odpowiednio
wynoszą odpowiednio 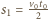 i
i 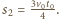 Maksymalna odległość, na jaką się oddalą, jest równa
Maksymalna odległość, na jaką się oddalą, jest równa 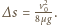
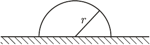
 zakopana jest do połowy w ziemi. Z jaką minimalną prędkością powinna odbić się od ziemi żaba, która chce przeskoczyć przez tę rurę?
zakopana jest do połowy w ziemi. Z jaką minimalną prędkością powinna odbić się od ziemi żaba, która chce przeskoczyć przez tę rurę?
 żaby w punkcie styczności tworzy z poziomem kąt
żaby w punkcie styczności tworzy z poziomem kąt  Z równań ruchu dla rzutu ukośnego otrzymujemy związek
Z równań ruchu dla rzutu ukośnego otrzymujemy związek 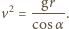 Zasada zachowania energii ma postać
Zasada zachowania energii ma postać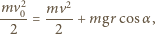
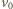 jest prędkością żaby w chwili odbicia. Aby znaleźć jej wartość minimalną, musimy odpowiedzieć na pytanie, dla jakiego kąta
jest prędkością żaby w chwili odbicia. Aby znaleźć jej wartość minimalną, musimy odpowiedzieć na pytanie, dla jakiego kąta 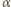 funkcja
funkcja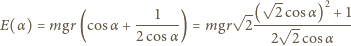
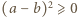 i wynikającej z niej
i wynikającej z niej 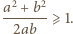 Widzimy, że energia jest minimalna, gdy
Widzimy, że energia jest minimalna, gdy 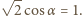 Szukana minimalna prędkość żaby wynosi
Szukana minimalna prędkość żaby wynosi 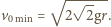 Dla kąta
Dla kąta 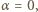 gdy tor żaby styka się w najwyższym punkcie z rurą,
gdy tor żaby styka się w najwyższym punkcie z rurą, 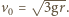
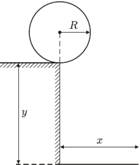
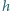 (rysunek) leży jednorodna kula o promieniu
(rysunek) leży jednorodna kula o promieniu 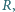 przy czym
przy czym 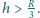 W stanie początkowym kula znajduje się w stanie równowagi chwiejnej. Znaleźć odległość
W stanie początkowym kula znajduje się w stanie równowagi chwiejnej. Znaleźć odległość 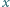 miejsca upadku kuli na ziemię, zakładając, że jej ruch rozpoczął się z zerową prędkością początkową. Nie ma tarcia między kulą a uskokiem.
miejsca upadku kuli na ziemię, zakładając, że jej ruch rozpoczął się z zerową prędkością początkową. Nie ma tarcia między kulą a uskokiem.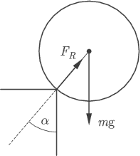
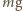 oraz siła reakcji podłoża
oraz siła reakcji podłoża 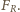 Ponieważ nie ma tarcia, siła reakcji skierowana jest wzdłuż promienia kuli. Obie siły mają zerowy moment względem środka kuli, zatem kula porusza się ruchem postępowym. Środek masy kuli porusza się po okręgu o promieniu
Ponieważ nie ma tarcia, siła reakcji skierowana jest wzdłuż promienia kuli. Obie siły mają zerowy moment względem środka kuli, zatem kula porusza się ruchem postępowym. Środek masy kuli porusza się po okręgu o promieniu 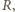 a jego równanie ruchu ma postać:
a jego równanie ruchu ma postać: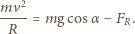
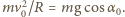 Z zasady zachowania energii mamy
Z zasady zachowania energii mamy 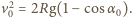 W chwili oderwania kąt
W chwili oderwania kąt 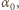 jaki tworzy prędkość kuli z poziomem, dany jest wzorem
jaki tworzy prędkość kuli z poziomem, dany jest wzorem 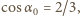 wartość prędkości wynosi
wartość prędkości wynosi 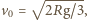 a dolny punkt kuli znajduje się na wysokości
a dolny punkt kuli znajduje się na wysokości 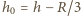 nad ziemią. Po oderwaniu środek masy kuli porusza się w kierunku poziomym ze stałą prędkością
nad ziemią. Po oderwaniu środek masy kuli porusza się w kierunku poziomym ze stałą prędkością 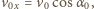 w kierunku pionowym spada w polu ciężkości z prędkością początkową
w kierunku pionowym spada w polu ciężkości z prędkością początkową 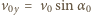 i osiąga prędkość
i osiąga prędkość 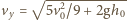 po czasie
po czasie 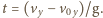 Szukana odległość dana jest wzorem
Szukana odległość dana jest wzorem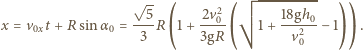
 zawieszony jest w polu ciężkości na nieważkiej sprężynie o współczynniku sprężystości
zawieszony jest w polu ciężkości na nieważkiej sprężynie o współczynniku sprężystości 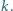 Długość nierozciągniętej sprężyny jest zaniedbywalna. Sprężynę odchylono do poziomu, rozciągnięto do długości
Długość nierozciągniętej sprężyny jest zaniedbywalna. Sprężynę odchylono do poziomu, rozciągnięto do długości 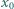 i puszczono swobodnie. Znaleźć najmniejszą długość sprężyny podczas ruchu.
i puszczono swobodnie. Znaleźć najmniejszą długość sprężyny podczas ruchu.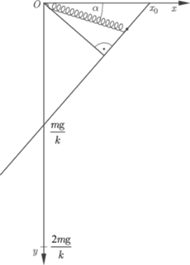
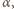 a jej długość wynosi
a jej długość wynosi 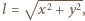 siły działające na ciężarek w kierunku poziomym i pionowym mają postać
siły działające na ciężarek w kierunku poziomym i pionowym mają postać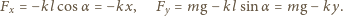
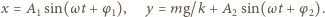
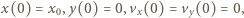 otrzymujemy
otrzymujemy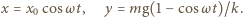
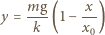
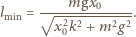

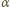 kąt między prędkością
kąt między prędkością  i maksymalną siłą tarcia
i maksymalną siłą tarcia 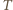 w pewnej chwili podczas rozpędzania. Równania ruchu motocyklisty w kierunku stycznym i prostopadłym do toru mają postać:
w pewnej chwili podczas rozpędzania. Równania ruchu motocyklisty w kierunku stycznym i prostopadłym do toru mają postać: 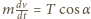 oraz
oraz 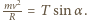 Różniczkując względem czasu drugie równanie i uwzględniając pierwsze, otrzymujemy:
Różniczkując względem czasu drugie równanie i uwzględniając pierwsze, otrzymujemy: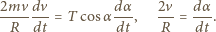
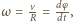 stąd
stąd 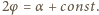 W chwili początkowej
W chwili początkowej 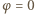 i
i 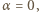 zatem
zatem 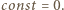 Gdy motocyklista osiąga maksymalną prędkość,
Gdy motocyklista osiąga maksymalną prędkość, 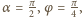 co odpowiada
co odpowiada 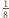 okręgu.
okręgu.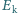 elektronu poruszającego się po okręgu o promieniu
elektronu poruszającego się po okręgu o promieniu 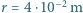 w polu magnetycznym o indukcji
w polu magnetycznym o indukcji 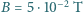 ? Masa spoczynkowa elektronu to
? Masa spoczynkowa elektronu to 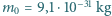 .
.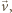 wartość prędkości nie zmienia się i dla rozważanego przypadku można równanie ruchu napisać w postaci
wartość prędkości nie zmienia się i dla rozważanego przypadku można równanie ruchu napisać w postaci 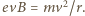 Stąd pęd jest równy
Stąd pęd jest równy 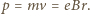 Należy teraz rozstrzygnąć, czy w rozpatrywanym przypadku elektron należy traktować jako cząstkę relatywistyczną, od tego bowiem zależy relacja pomiędzy
Należy teraz rozstrzygnąć, czy w rozpatrywanym przypadku elektron należy traktować jako cząstkę relatywistyczną, od tego bowiem zależy relacja pomiędzy 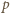 i
i 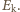 Podstawiając wartości do wzoru na pęd, dostajemy
Podstawiając wartości do wzoru na pęd, dostajemy 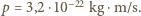 Dla elektronu
Dla elektronu 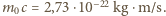 Nie zachodzi więc relacja
Nie zachodzi więc relacja 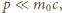 co pozwoliłoby stosować "zwykłe", nierelatywistyczne wzory. Używając wzoru relatywistycznego
co pozwoliłoby stosować "zwykłe", nierelatywistyczne wzory. Używając wzoru relatywistycznego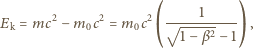
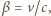 dostajemy
dostajemy 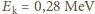 .
.
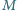 spoczywa na powierzchni poziomej, a mała kulka o masie
spoczywa na powierzchni poziomej, a mała kulka o masie  porusza się z prędkością
porusza się z prędkością  wewnątrz ramki, równolegle do boku o długości
wewnątrz ramki, równolegle do boku o długości  Kulka zderza się sprężyście ze środkami krótszych boków ramki. Znaleźć czas pomiędzy kolejnymi zderzeniami z tym samym bokiem ramki. Nie ma tarcia.
Kulka zderza się sprężyście ze środkami krótszych boków ramki. Znaleźć czas pomiędzy kolejnymi zderzeniami z tym samym bokiem ramki. Nie ma tarcia.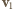 i
i 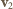 spełniają związki:
spełniają związki: 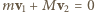 ,
, 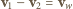 , gdzie
, gdzie 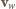 jest prędkością względną. Stąd
jest prędkością względną. Stąd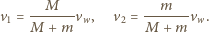
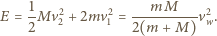
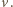 Szukany czas między dwoma kolejnymi zderzeniami wynosi
Szukany czas między dwoma kolejnymi zderzeniami wynosi 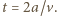
 pod kątem
pod kątem  do poziomu. Po narysowanej krzywej pełznie mały żuczek, którego prędkość ma stałą wartość
do poziomu. Po narysowanej krzywej pełznie mały żuczek, którego prędkość ma stałą wartość  Ile wynosi przyspieszenie żuczka w punkcie odpowiadającym maksymalnej wysokości, na jaką wzniósł się kamień. Oporu powietrza podczas ruchu kamienia nie uwzględniamy.
Ile wynosi przyspieszenie żuczka w punkcie odpowiadającym maksymalnej wysokości, na jaką wzniósł się kamień. Oporu powietrza podczas ruchu kamienia nie uwzględniamy.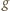 jest prostopadłe do toru i jest przyspieszeniem dośrodkowym:
jest prostopadłe do toru i jest przyspieszeniem dośrodkowym: 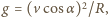 gdzie
gdzie 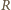 jest promieniem krzywizny toru w rozważanym punkcie. Promień krzywizny toru w odpowiadającym punkcie na rysunku wynosi
jest promieniem krzywizny toru w rozważanym punkcie. Promień krzywizny toru w odpowiadającym punkcie na rysunku wynosi 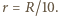 Przyspieszenie żuczka jest prostopadłe do toru (bo jego wartość prędkości jest stała) i wynosi
Przyspieszenie żuczka jest prostopadłe do toru (bo jego wartość prędkości jest stała) i wynosi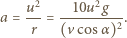
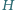 na nieruchomą rakietkę odbija się na wysokość
na nieruchomą rakietkę odbija się na wysokość 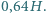 Chłopiec podbija periodycznie taką piłeczkę pionowo do góry tak, że po każdym uderzeniu wznosi się ona na wysokość
Chłopiec podbija periodycznie taką piłeczkę pionowo do góry tak, że po każdym uderzeniu wznosi się ona na wysokość 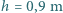 powyżej rakietki. Z jaką prędkością rakietka porusza się ku górze w momencie uderzenia? Przyjmujemy, że masa rakietki jest dużo większa od masy piłeczki.
powyżej rakietki. Z jaką prędkością rakietka porusza się ku górze w momencie uderzenia? Przyjmujemy, że masa rakietki jest dużo większa od masy piłeczki.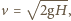 gdzie
gdzie 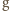 to przyspieszenie ziemskie. Po odbiciu piłeczka uzyskuje prędkość
to przyspieszenie ziemskie. Po odbiciu piłeczka uzyskuje prędkość 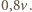 Niech teraz rakietka w momencie odbicia piłeczki porusza się ku górze z prędkością
Niech teraz rakietka w momencie odbicia piłeczki porusza się ku górze z prędkością 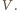 W układzie współrzędnych, związanym z rakietką, piłeczka ma w momencie zderzenia prędkość
W układzie współrzędnych, związanym z rakietką, piłeczka ma w momencie zderzenia prędkość 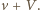 Po zderzeniu jej prędkość w tym układzie odniesienia wyniesie
Po zderzeniu jej prędkość w tym układzie odniesienia wyniesie 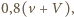 czyli w nieruchomym układzie odniesienia będzie miała prędkość
czyli w nieruchomym układzie odniesienia będzie miała prędkość 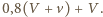 Ponieważ po podbiciu piłeczka ma się wznieść na taką wysokość, z jakiej spadła, to musi być spełniona zależność
Ponieważ po podbiciu piłeczka ma się wznieść na taką wysokość, z jakiej spadła, to musi być spełniona zależność 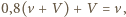 a stąd
a stąd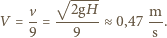

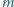 połączonych nieważką sprężyną o współczynniku sprężystości
połączonych nieważką sprężyną o współczynniku sprężystości 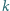 znajduje się w stanie równowagi. Górną płytkę naciśnięto tak, że opuściła się ona o
znajduje się w stanie równowagi. Górną płytkę naciśnięto tak, że opuściła się ona o 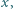 a następnie puszczono. Na jaką maksymalną wysokość podniósł się środek masy układu?
a następnie puszczono. Na jaką maksymalną wysokość podniósł się środek masy układu?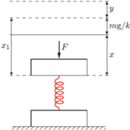
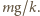 Dolna płytka oderwie się od podłoża, gdy siła
Dolna płytka oderwie się od podłoża, gdy siła 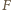 powodująca dodatkowe ściśnięcie sprężyny o
powodująca dodatkowe ściśnięcie sprężyny o 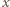 będzie większa od ciężaru układu, czyli spełniony będzie warunek
będzie większa od ciężaru układu, czyli spełniony będzie warunek 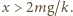 W chwili oderwania sprężyna będzie wydłużona o
W chwili oderwania sprężyna będzie wydłużona o 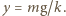 Prędkość
Prędkość  górnej płytki w chwili oderwania dolnej znajdujemy z zasady zachowania energii:
górnej płytki w chwili oderwania dolnej znajdujemy z zasady zachowania energii: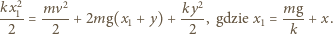
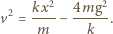
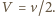 Po oderwaniu środek masy porusza się ruchem jednostajnie opóźnionym i wznosi się na wysokość
Po oderwaniu środek masy porusza się ruchem jednostajnie opóźnionym i wznosi się na wysokość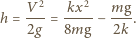
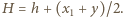 Jeśli
Jeśli 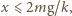 dolna płytka pozostaje w spoczynku, a górna porusza się ruchem harmonicznym wokół położenia równowagi z amplitudą
dolna płytka pozostaje w spoczynku, a górna porusza się ruchem harmonicznym wokół położenia równowagi z amplitudą 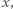 czyli wznosi się na maksymalną wysokość
czyli wznosi się na maksymalną wysokość 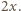 Zatem odpowiedź na postawione pytanie jest następująca: maksymalna wysokość, na jaką wzniesie się środek masy układu, dana jest wzorem:
Zatem odpowiedź na postawione pytanie jest następująca: maksymalna wysokość, na jaką wzniesie się środek masy układu, dana jest wzorem: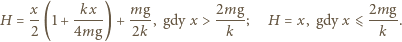
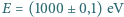 - tzn. pomiar wykonano z dokładnością do
- tzn. pomiar wykonano z dokładnością do 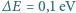 . Wyznacz stosunek dokładności określenia położenia (współrzędnej
. Wyznacz stosunek dokładności określenia położenia (współrzędnej  w kierunku ruchu) elektronu do długości jego fali de Broglie'a bezpośrednio po tym pomiarze.
w kierunku ruchu) elektronu do długości jego fali de Broglie'a bezpośrednio po tym pomiarze.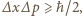 gdzie
gdzie 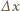 i
i 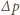 to odpowiednio dokładność pomiaru współrzędnej
to odpowiednio dokładność pomiaru współrzędnej 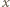 i pędu
i pędu 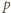 w kierunku
w kierunku 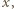 a
a 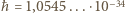 Js jest stałą Plancka
Js jest stałą Plancka 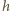 podzieloną przez
podzieloną przez 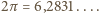
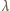 fali de Broglie'a cząstki o pędzie
fali de Broglie'a cząstki o pędzie 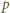 wynosi
wynosi 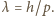 Mamy więc
Mamy więc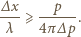
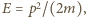 gdzie
gdzie  oznacza masę cząstki. Stąd w przybliżeniu mamy
oznacza masę cząstki. Stąd w przybliżeniu mamy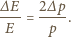


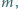 do którego doczepiono nieważką sprężynę o współczynniku sprężystości
do którego doczepiono nieważką sprężynę o współczynniku sprężystości 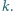 W pewnej chwili wolny koniec sprężyny zaczęto ciągnąć tak, że poruszał się on ze stałą poziomą prędkością
W pewnej chwili wolny koniec sprężyny zaczęto ciągnąć tak, że poruszał się on ze stałą poziomą prędkością  Jaką drogę przebędzie klocek do momentu, w którym osiągnie on prędkość
Jaką drogę przebędzie klocek do momentu, w którym osiągnie on prędkość 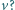 Współczynniki tarcia statycznego i kinetycznego między klockiem a podłożem wynoszą odpowiednio
Współczynniki tarcia statycznego i kinetycznego między klockiem a podłożem wynoszą odpowiednio 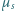 i
i 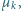 przy czym
przy czym 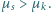
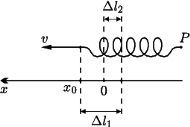
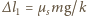 i przyjmijmy tę chwilę za początkową. W układzie odniesienia związanym ze swobodnym końcem
i przyjmijmy tę chwilę za początkową. W układzie odniesienia związanym ze swobodnym końcem 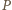 sprężyny klocek zacznie oddalać się ruchem harmonicznym od położenia równowagi (
sprężyny klocek zacznie oddalać się ruchem harmonicznym od położenia równowagi ( 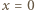 na rysunku), gdzie wydłużenie sprężyny wynosi
na rysunku), gdzie wydłużenie sprężyny wynosi 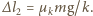 W chwili początkowej prędkość klocka wynosi
W chwili początkowej prędkość klocka wynosi 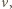 a jego odległość od położenia równowagi jest równa
a jego odległość od położenia równowagi jest równa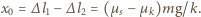
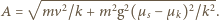
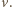 Ruch klocka do chwili, gdy oddali się na maksymalną odległość
Ruch klocka do chwili, gdy oddali się na maksymalną odległość 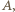 opisuje wzór
opisuje wzór 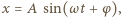 gdzie
gdzie 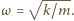 Z warunku początkowego
Z warunku początkowego 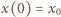 otrzymujemy przesunięcie fazowe
otrzymujemy przesunięcie fazowe 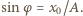 Czas
Czas 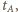 po którym odległość od położenia równowagi osiągnie wartość
po którym odległość od położenia równowagi osiągnie wartość 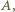 dostajemy ze wzoru
dostajemy ze wzoru 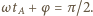 Odległość klocka od położenia początkowego w układzie związanym z końcem sprężyny równa jest
Odległość klocka od położenia początkowego w układzie związanym z końcem sprężyny równa jest 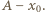 Szukana droga przebyta przez klocek w układzie związanym z podłożem wynosi
Szukana droga przebyta przez klocek w układzie związanym z podłożem wynosi 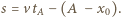

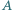 prostokątnej studni o szerokości
prostokątnej studni o szerokości 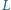 i głębokości
i głębokości 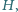 aby w wyniku odbicia od jej dna trafiła dokładnie w jej przeciwną krawędź
aby w wyniku odbicia od jej dna trafiła dokładnie w jej przeciwną krawędź 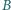 (rysunek)? Przyjąć, że ścianki i dno studni są doskonale gładkie, odbicia są doskonale sprężyste i można zaniedbać wszelkie straty energii.
(rysunek)? Przyjąć, że ścianki i dno studni są doskonale gładkie, odbicia są doskonale sprężyste i można zaniedbać wszelkie straty energii.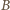 po jednym lub większej liczbie odbić od dna i towarzyszących im ewentualnie odbiciach od ścianek studni. Jeżeli nastąpiło
po jednym lub większej liczbie odbić od dna i towarzyszących im ewentualnie odbiciach od ścianek studni. Jeżeli nastąpiło 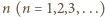 odbić od dna, to kulka znajdzie się na wysokości
odbić od dna, to kulka znajdzie się na wysokości 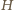 od dna studni po czasie
od dna studni po czasie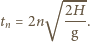
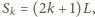 gdzie
gdzie 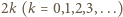 jest liczbą uderzeń kulki o pionowe ścianki studni. Stąd otrzymujemy, że prędkość kulki w punkcie
jest liczbą uderzeń kulki o pionowe ścianki studni. Stąd otrzymujemy, że prędkość kulki w punkcie 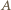 powinna być równa:
powinna być równa: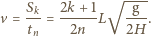
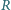 naciągnięto ciasny, gumowy pierścień. Siła rozciągająca pierścień wynosi
naciągnięto ciasny, gumowy pierścień. Siła rozciągająca pierścień wynosi 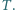 Jaką siłę trzeba przyłożyć, aby przesunąć pierścień, bez obrotu, wzdłuż osi walca? Współczynnik tarcia między stalą i gumą wynosi
Jaką siłę trzeba przyłożyć, aby przesunąć pierścień, bez obrotu, wzdłuż osi walca? Współczynnik tarcia między stalą i gumą wynosi 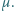 Przyjąć, że siła przesuwająca jest rozłożona równomiernie wzdłuż pierścienia.
Przyjąć, że siła przesuwająca jest rozłożona równomiernie wzdłuż pierścienia.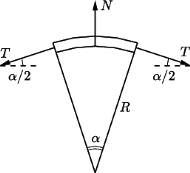
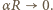 Na każdy odcinek działają siły naciągu pierścienia
Na każdy odcinek działają siły naciągu pierścienia 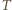 i reakcji walca
i reakcji walca 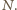 Ich suma jest równa zero, bo pierścień nie obraca się. Stąd
Ich suma jest równa zero, bo pierścień nie obraca się. Stąd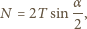
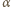 daje
daje 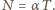 Stąd możemy obliczyć siłę tarcia, działającą na taki odcinek, przy przesuwaniu pierścienia wzdłuż walca:
Stąd możemy obliczyć siłę tarcia, działającą na taki odcinek, przy przesuwaniu pierścienia wzdłuż walca: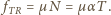
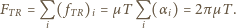
 poruszającego się z prędkością
poruszającego się z prędkością  po orbicie kołowej w pobliżu powierzchni Ziemi działa stała siła hamująca
po orbicie kołowej w pobliżu powierzchni Ziemi działa stała siła hamująca 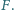 Znając przyspieszenie ziemskie
Znając przyspieszenie ziemskie 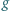 znaleźć prędkość
znaleźć prędkość 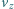 zniżania się satelity, przyjmując, że zmiana jego orbity zachodzi dostatecznie wolno.
zniżania się satelity, przyjmując, że zmiana jego orbity zachodzi dostatecznie wolno.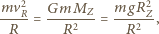
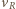 - prędkość satelity na orbicie kołowej o promieniu
- prędkość satelity na orbicie kołowej o promieniu 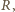
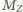 - masa Ziemi,
- masa Ziemi, 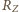 - jej promień. Załóżmy, że w ciągu krótkiego czasu
- jej promień. Załóżmy, że w ciągu krótkiego czasu 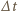 promień orbity zmniejszył się o
promień orbity zmniejszył się o 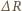 pod wpływem siły
pod wpływem siły 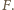 Z zasady zachowania energii mamy związek
Z zasady zachowania energii mamy związek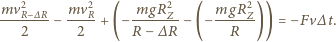
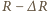 z prędkością
z prędkością 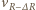 ma postać
ma postać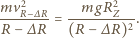
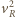 i
i 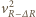 z zależności (1) i (3) i podstawiając je do zależności (2) otrzymujemy
z zależności (1) i (3) i podstawiając je do zależności (2) otrzymujemy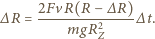
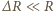 oraz
oraz 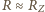 znajdujemy prędkość zniżania się satelity
znajdujemy prędkość zniżania się satelity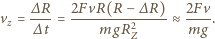

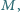 do którego przymocowany jest nieważki, nieruchomy bloczek, może ślizgać się po poziomej powierzchni. Przez bloczek przerzucona jest nić, której jeden koniec jest poziomy i przymocowany do ściany, a na drugim końcu zawieszony jest ciężarek. W chwili początkowej ciężarek odchylono od pionu o kąt
do którego przymocowany jest nieważki, nieruchomy bloczek, może ślizgać się po poziomej powierzchni. Przez bloczek przerzucona jest nić, której jeden koniec jest poziomy i przymocowany do ściany, a na drugim końcu zawieszony jest ciężarek. W chwili początkowej ciężarek odchylono od pionu o kąt 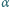 i puszczono. Znaleźć masę ciężarka, jeśli kąt odchylenia nici od pionu nie zmienia się podczas ruchu klocka. Tarcie zaniedbujemy.
i puszczono. Znaleźć masę ciężarka, jeśli kąt odchylenia nici od pionu nie zmienia się podczas ruchu klocka. Tarcie zaniedbujemy.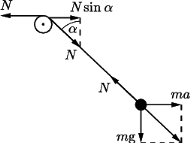
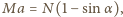 gdzie
gdzie 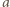 jest przyspieszeniem klocka, a
jest przyspieszeniem klocka, a 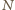 siłą naprężenia nici. W układzie związanym z klockiem ciężarek porusza się z przyspieszeniem
siłą naprężenia nici. W układzie związanym z klockiem ciężarek porusza się z przyspieszeniem 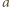 wzdłuż prostej, która tworzy z pionem kąt
wzdłuż prostej, która tworzy z pionem kąt 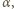 pod działaniem sił przedstawionych na rysunku obok. Jego równanie ruchu ma postać:
pod działaniem sił przedstawionych na rysunku obok. Jego równanie ruchu ma postać: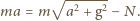
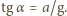 Rozwiązując przedstawione równania, otrzymujmy masę ciężarka:
Rozwiązując przedstawione równania, otrzymujmy masę ciężarka: