Klub 44F - zadania X 2015»Zadanie 605
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania X 2015
- Publikacja w Delcie: październik 2015
- Publikacja elektroniczna: 30 września 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (92 KB)
Linie widma promieniowania elektromagnetycznego wysyłanego przez atomy deuteru są nieznacznie przesunięte w stosunku do analogicznych linii emitowanych przez standardowy wodór (z protonem jako jądrem atomu). Jaką prędkość  ruchu przypisze atomowi astronom, jeśli badał widmo spoczywającego deuteru w przekonaniu, że to wodór? Masa elektronu
ruchu przypisze atomowi astronom, jeśli badał widmo spoczywającego deuteru w przekonaniu, że to wodór? Masa elektronu 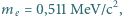 masa protonu
masa protonu 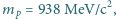 masa deuteronu (jądra deuteru)
masa deuteronu (jądra deuteru) 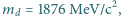 a prędkość światła
a prędkość światła 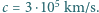
Najniższe przełożenie, jakim dysponuje rowerzysta w swoim rowerze, składa się z zębatek o 28 ząbkach z tyłu i 22 z przodu. Masa roweru stanowi 20% masy rowerzysty, długość korby to 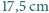 , a promień koła
, a promień koła 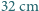 . Jaki jest największy kąt nachylenia zbocza, pod jakie rowerzysta ma szansę podjechać, używając zwykłych pedałów, bez nosków i zatrzasków? Jaki warunek powinien spełniać współczynnik tarcia statycznego
. Jaki jest największy kąt nachylenia zbocza, pod jakie rowerzysta ma szansę podjechać, używając zwykłych pedałów, bez nosków i zatrzasków? Jaki warunek powinien spełniać współczynnik tarcia statycznego 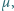 aby koło toczyło się po powierzchni bez poślizgu?
aby koło toczyło się po powierzchni bez poślizgu?
Z południowego i z północnego bieguna ziemskiego wystrzelono równocześnie rakiety z jednakowymi prędkościami początkowymi, skierowanymi poziomo. Po 3 godzinach i 20 minutach rakiety znalazły się w maksymalnej odległości od siebie. Znaleźć tę maksymalną odległość. Przyjąć, że przyspieszenie ziemskie wynosi 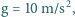 a Ziemia jest kulą o promieniu
a Ziemia jest kulą o promieniu 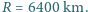
Koło, którego cała masa rozłożona jest równomiernie na obwodzie, może obracać się bez tarcia wokół swojej osi skierowanej poziomo. Wewnątrz koła, wzdłuż jego obwodu biegnie wiewiórka. Współczynnik tarcia między kołem a wiewiórką wynosi 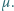 Stosunek masy koła do masy wiewiórki równy jest
Stosunek masy koła do masy wiewiórki równy jest 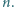 Jakie maksymalne, stałe przyspieszenie liniowe może nadać kołu wiewiórka?
Jakie maksymalne, stałe przyspieszenie liniowe może nadać kołu wiewiórka?
W sytuacji opisanej w zadaniu ZF-875 zawias został zamocowany pod suwakiem pozwalającym na swobodne przemieszczanie się zawiasu po poziomej belce (leżącej w płaszczyźnie płyty). Z jaką siłą zawias będzie działał na płytę i jakie będzie przyspieszenie suwaka w chwili zwolnienia elektromagnesu? W jakiej pozycji zatrzyma się suwak, gdy jego opory ruchu można zaniedbać w porównaniu do pozostałych oporów ruchu (które należy uznać za minimalne: ich początkowy wpływ zaniedbujemy, ale oczekujemy, że dzięki nim płyta w końcu znieruchomieje).
Jednorodna żelazna kwadratowa płyta o masie  i boku
i boku 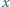 (oraz nieistotnej dla problemu grubości) wisi na przymocowanym do jej rogu zawiasie (umożliwiającym obrót płyty w jej płaszczyźnie) i jest dodatkowo przytrzymana elektromagnesem tak, że jej górna krawędź jest pozioma. Wyznaczyć siłę, z jaką zawias działa na płytę w chwili zwolnienia elektromagnesu. Jako wprawkę należy wyprowadzić wzór na moment bezwładności takiej płyty (względem dowolnej osi prostopadłej do jej płaszczyzny), wykorzystując tylko analizę wymiarową i twierdzenie Steinera.
(oraz nieistotnej dla problemu grubości) wisi na przymocowanym do jej rogu zawiasie (umożliwiającym obrót płyty w jej płaszczyźnie) i jest dodatkowo przytrzymana elektromagnesem tak, że jej górna krawędź jest pozioma. Wyznaczyć siłę, z jaką zawias działa na płytę w chwili zwolnienia elektromagnesu. Jako wprawkę należy wyprowadzić wzór na moment bezwładności takiej płyty (względem dowolnej osi prostopadłej do jej płaszczyzny), wykorzystując tylko analizę wymiarową i twierdzenie Steinera.

Żuk pełznie po sztywnej słomce, opartej o gładką podłogę i gładką pionową ściankę. Słomka jest jednorodna, tworzy z poziomem kąt 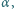 jej długość wynosi
jej długość wynosi 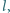 masa słomki jest zaniedbywalna w porównaniu z masą żuka
masa słomki jest zaniedbywalna w porównaniu z masą żuka  Prędkość początkowa żuka w punkcie
Prędkość początkowa żuka w punkcie 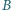 wynosi
wynosi 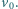 Jak musi poruszać się żuk, aby słomka pozostawała nieruchoma? Po jakim czasie dopełznie on do punktu
Jak musi poruszać się żuk, aby słomka pozostawała nieruchoma? Po jakim czasie dopełznie on do punktu 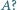
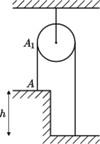
Cienki, nierozciągliwy łańcuszek o zaniedbywalnie małych ogniwach przerzucony jest przez nieruchomy bloczek. Końce zwisających z bloczka części łańcuszka leżą na stole i na podłodze, przy czym część leżąca na stole jest wystarczająco długa i ułożona w mały kopczyk wokół punktu 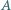 (odcinek
(odcinek 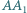 jest pionowy). Znaleźć ustaloną prędkość wiszącej części łańcuszka. Blat stołu znajduje się na wysokości
jest pionowy). Znaleźć ustaloną prędkość wiszącej części łańcuszka. Blat stołu znajduje się na wysokości 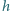 nad podłogą. Tarcie zaniedbujemy.
nad podłogą. Tarcie zaniedbujemy.
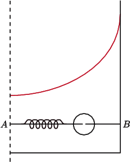
W naczyniu w kształcie walca znajduje się ciecz o gęstości 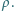 Walec obraca się ze stałą prędkością kątową
Walec obraca się ze stałą prędkością kątową 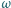 wokół własnej osi. Wewnątrz walca, wzdłuż jego promienia, umocowany jest cienki pręt
wokół własnej osi. Wewnątrz walca, wzdłuż jego promienia, umocowany jest cienki pręt 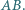 Po pręcie może ślizgać się bez tarcia koralik w kształcie kuli o masie
Po pręcie może ślizgać się bez tarcia koralik w kształcie kuli o masie  i promieniu
i promieniu 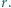 Kula połączona jest z końcem
Kula połączona jest z końcem 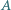 pręta za pomocą sprężyny o współczynniku sprężystości
pręta za pomocą sprężyny o współczynniku sprężystości 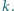 Długość nieodkształconej sprężyny wynosi
Długość nieodkształconej sprężyny wynosi 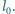 Znaleźć odległość środka kuli od osi obrotu.
Znaleźć odległość środka kuli od osi obrotu.
Jedną z "atrakcji" wesołego miasteczka jest duża, pozioma tarcza o promieniu 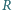 wirująca z prędkością kątową
wirująca z prędkością kątową 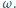 Pracownik wesołego miasteczka założył się z kolegami, że startując ze środka tarczy i idąc ze stałą prędkością wzdłuż wymalowanego na tarczy promienia dotrze do brzegu tarczy w chwili, gdy wykona ona połowę obrotu. Czy wygra zakład, jeśli współczynnik tarcia między powierzchnią tarczy i podeszwami butów pracownika wynosi
Pracownik wesołego miasteczka założył się z kolegami, że startując ze środka tarczy i idąc ze stałą prędkością wzdłuż wymalowanego na tarczy promienia dotrze do brzegu tarczy w chwili, gdy wykona ona połowę obrotu. Czy wygra zakład, jeśli współczynnik tarcia między powierzchnią tarczy i podeszwami butów pracownika wynosi 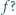

Na powierzchni nachylonej do pionu pod małym kątem  zawieszono na nierozciągliwej, nieważkiej nici o długości
zawieszono na nierozciągliwej, nieważkiej nici o długości 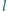 kulkę o masie
kulkę o masie  Kulkę wychylono w lewo o mały kąt
Kulkę wychylono w lewo o mały kąt 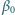 większy od
większy od 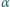 (Rys. 3) i puszczono. Właściwości sprężyste kulki i powierzchni są takie, że stosunek energii kinetycznej kulki bezpośrednio po zderzeniu do jej energii kinetycznej bezpośrednio przed zderzeniem wynosi
(Rys. 3) i puszczono. Właściwości sprężyste kulki i powierzchni są takie, że stosunek energii kinetycznej kulki bezpośrednio po zderzeniu do jej energii kinetycznej bezpośrednio przed zderzeniem wynosi 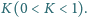 Jaki będzie maksymalny kąt dla kolejnych wychyleń kulki w lewo?
Jaki będzie maksymalny kąt dla kolejnych wychyleń kulki w lewo?

W układzie przedstawionym na rysunku bloki mają zaniedbywalnie małe masy, nić jest nieważka i nierozciągliwa, fragmenty nici, które nie leżą na blokach, są poziome. Masy klocków leżących na poziomej powierzchni są takie same i równe 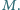 Do końca nici przyłożono poziomą siłę
Do końca nici przyłożono poziomą siłę 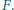 Z jakim przyspieszeniem porusza się ten koniec nici? Załóż brak tarcia i przyjmij, że klocki poruszają się ruchem postępowym.
Z jakim przyspieszeniem porusza się ten koniec nici? Załóż brak tarcia i przyjmij, że klocki poruszają się ruchem postępowym.
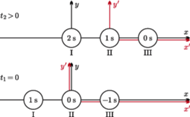
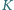 i
i 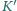 to inercjalne układy odniesienia o zgodnych osiach,
to inercjalne układy odniesienia o zgodnych osiach, 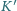 porusza się z prędkością
porusza się z prędkością 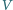 względem
względem 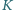 wzdłuż osi
wzdłuż osi  Wzdłuż tej osi w układzie
Wzdłuż tej osi w układzie 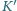 rozmieszczony jest ciąg jednakowych, równo odległych i zsynchronizowanych zegarów. Obserwator w
rozmieszczony jest ciąg jednakowych, równo odległych i zsynchronizowanych zegarów. Obserwator w 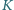 notuje równoczesne dla niego wskazania tych zegarów w dwóch chwilach:
notuje równoczesne dla niego wskazania tych zegarów w dwóch chwilach: 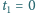 i
i 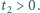 Na podstawie tych pomiarów wyznaczyć
Na podstawie tych pomiarów wyznaczyć 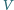 oraz odległość
oraz odległość 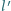 między sąsiednimi zegarami mierzoną w
między sąsiednimi zegarami mierzoną w 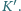
Okolice biegunów planety pokrywały kiedyś czapy lądolodów od każdego z biegunów aż do szerokości geograficznej 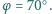 Niestety, nieostrożne spalanie paliw kopalnych przez mieszkańców okolic o umiarkowanym klimacie spowodowało wzrost temperatury atmosfery (tzw. efekt cieplarniany) i stopienie obu okołobiegunowych lądolodów. O ile zmieniła się długość doby jeśli początkowo doba trwała
Niestety, nieostrożne spalanie paliw kopalnych przez mieszkańców okolic o umiarkowanym klimacie spowodowało wzrost temperatury atmosfery (tzw. efekt cieplarniany) i stopienie obu okołobiegunowych lądolodów. O ile zmieniła się długość doby jeśli początkowo doba trwała 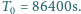 Masa planety wynosi
Masa planety wynosi 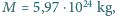 jej promień
jej promień 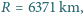 a masa lądolodów
a masa lądolodów 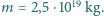 Załóż, że planeta jest niemal idealną kulą.
Załóż, że planeta jest niemal idealną kulą.
Na Ziemi najwyższe podskoki odpowiadają podniesieniu środka ciężkości człowieka o około 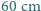 . Jaki jest największy promień skalnej planetoidy, od której przyciągania człowiek mógłby uwolnić się o własnych siłach? Średni promień Ziemi wynosi
. Jaki jest największy promień skalnej planetoidy, od której przyciągania człowiek mógłby uwolnić się o własnych siłach? Średni promień Ziemi wynosi 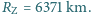 Przyjmij, że średnia gęstość planetoidy jest równa średniej gęstości Ziemi.
Przyjmij, że średnia gęstość planetoidy jest równa średniej gęstości Ziemi.
Kółko powstałe ze sprężyny o długości początkowej
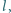 współczynniku
sprężystości
współczynniku
sprężystości
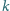 i masie
i masie
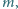 której końce połączono,
wiruje z prędkością kątową
której końce połączono,
wiruje z prędkością kątową
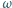 wokół osi prostopadłej do jego
płaszczyzny i przechodzącej przez jego środek. Jak zależy promień
kółka
wokół osi prostopadłej do jego
płaszczyzny i przechodzącej przez jego środek. Jak zależy promień
kółka
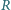 od prędkości
od prędkości
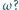 Przyjąć, że średnica zwojów
sprężyny jest dużo mniejsza od jej długości.
Przyjąć, że średnica zwojów
sprężyny jest dużo mniejsza od jej długości.
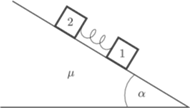
Z równi pochyłej nachylonej do poziomu pod kątem
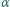 zsuwają się dwa
klocki o jednakowych masach
zsuwają się dwa
klocki o jednakowych masach
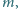 połączone nieważką sprężyną
o współczynniku sprężystości
połączone nieważką sprężyną
o współczynniku sprężystości
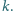 W chwili początkowej sprężyna jest
nieodkształcona, a prędkości klocków są równe zeru. Współczynnik
tarcia między drugim klockiem a równią wynosi
W chwili początkowej sprężyna jest
nieodkształcona, a prędkości klocków są równe zeru. Współczynnik
tarcia między drugim klockiem a równią wynosi
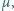 przy czym
przy czym
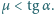 Między pierwszym klockiem a równią tarcia nie ma. Znaleźć
maksymalne wydłużenie sprężyny oraz inne wielkości charakteryzujące ruch
klocków.
Między pierwszym klockiem a równią tarcia nie ma. Znaleźć
maksymalne wydłużenie sprężyny oraz inne wielkości charakteryzujące ruch
klocków.

Baletnica wyrzuciła przed siebie obręcz o masie
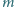 i promieniu
i promieniu
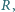 nadając jej początkowo prędkość kątową
nadając jej początkowo prędkość kątową
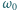 i prędkość
ruchu postępowego
i prędkość
ruchu postępowego
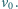 Obręcz ślizgała się przez pewien czas
Obręcz ślizgała się przez pewien czas
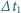 po parkiecie, po czym zatrzymała się i natychmiast zawróciła ku
baletnicy. Czas powrotu wynosił
po parkiecie, po czym zatrzymała się i natychmiast zawróciła ku
baletnicy. Czas powrotu wynosił
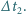 Dla jakiej wartości stosunku
Dla jakiej wartości stosunku
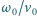 zachodzi równość
zachodzi równość
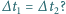 Współczynnik tarcia
obręczy o podłoże wynosi
Współczynnik tarcia
obręczy o podłoże wynosi
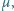 a moment bezwładności obręczy to
a moment bezwładności obręczy to
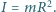
Przy jakiej wartości
 kąta nachylenia drogi do poziomu długość
drogi hamowania zjeżdżającego samochodu rośnie ponad dwukrotnie
w porównaniu z hamowaniem na odcinku poziomym? Przyjmujemy, że
współczynnik tarcia opon o asfalt wynosi
kąta nachylenia drogi do poziomu długość
drogi hamowania zjeżdżającego samochodu rośnie ponad dwukrotnie
w porównaniu z hamowaniem na odcinku poziomym? Przyjmujemy, że
współczynnik tarcia opon o asfalt wynosi
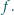
Pręt o długości
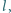 promieniu
promieniu
 i masie
i masie
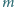 porusza się
wewnątrz pionowej rury o promieniu
porusza się
wewnątrz pionowej rury o promieniu
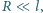 wypełnionej nieściśliwą
cieczą o gęstości
wypełnionej nieściśliwą
cieczą o gęstości
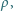 wzdłuż jej osi. Gęstość pręta jest mniejsza od
gęstości cieczy. Znaleźć przyspieszenie pręta. Opory ruchu (lepkość cieczy)
można zaniedbać.
wzdłuż jej osi. Gęstość pręta jest mniejsza od
gęstości cieczy. Znaleźć przyspieszenie pręta. Opory ruchu (lepkość cieczy)
można zaniedbać.
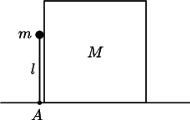
Nieważki pręt o długości
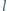 z niewielkim ciężarkiem o masie
z niewielkim ciężarkiem o masie
 na końcu może obracać się wokół punktu
na końcu może obracać się wokół punktu
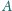 i znajduje się
w położeniu pionowym, dotykając klocka o masie
i znajduje się
w położeniu pionowym, dotykając klocka o masie
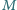 (rysunek).
W wyniku lekkiego popchnięcia układ zostaje wprawiony w ruch. Jaki musi
być stosunek mas
(rysunek).
W wyniku lekkiego popchnięcia układ zostaje wprawiony w ruch. Jaki musi
być stosunek mas
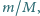 aby w chwili utraty kontaktu ciężarka
z klockiem pręt tworzył z poziomem kąt
aby w chwili utraty kontaktu ciężarka
z klockiem pręt tworzył z poziomem kąt
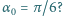 Ile będzie wynosić
w tym momencie prędkość klocka? Tarcie zaniedbać.
Ile będzie wynosić
w tym momencie prędkość klocka? Tarcie zaniedbać.