Kącik początkującego olimpijczyka
Rachunki
Szły raz drogą trzy sześciany
Tożsamości algebraiczne, w których pojawia się suma sześcianów trzech liczb.
Głównymi bohaterkami styczniowego kącika są następujące równości:
Każda z nich jest łatwa do udowodnienia przez wymnożenie i redukcję wyrazów podobnych po prawej stronie. Nie będziemy tu tego robić.
Z tożsamości (3) natychmiast wnioskujemy następujący
Lemat. Jeśli 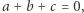 to
to 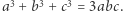
Można go również sformułować w postaci równości
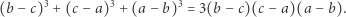 |
(4) |