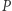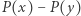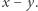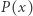Przeskocz do treści

Delta mi!

Temat » Matematyka » Algebra

Kącik początkującego olimpijczyka

Twierdzenie Bézouta

Bartłomiej Bzdęga

o artykule ...

  • Publikacja w Delcie: grudzień 2019
  • Publikacja elektroniczna: 30 listopada 2019
  • Wersja do druku [application/pdf]: (374 KB)

O licznych zastosowaniach faktu, że dla każdego wielomianu 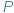|P w sumie algebraicznej 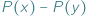P (x)− P (y) można wyłączyć przed nawias wyrażenie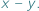 |x− y :

Rozważmy wielomian 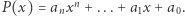n P (x) = anx + ...+ a1x + a0. Korzystając ze wzoru

k k k−1 k−2 k− 3 2 k− 2 k− 1 x − y = (x − y)(x + x y+ x y +...+ xy +y ),

możemy zapisać

P (x) −P (y) = (x − y)F(x, y), gdzieF(x, y) = Q ai+ j+1xiy j i, jE0

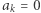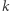(przyjmujemy, że ak = 0 dla |k większych od stopnia wielomianu 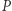|P). Dzięki tej tożsamości mamy trzy następujące twierdzenia.

Twierdzenie 1. Dla dowolnego wielomianu P w wyrażeniu |P(x) −P (y) można wyłączyć przed nawias różnicę |x −y.

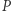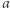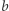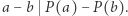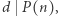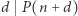Twierdzenie 2. Jeśli wielomian P ma współczynniki całkowite, to dla różnych liczb całkowitych |a i b zachodzi podzielność liczb całkowitych a −b P (a)− P(b). W szczególności, jeśli |d P(n), to |d P (n +d) dla całkowitych 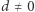|d ≠0 i |n.

Twierdzenie 3 (Bézouta). Wielomian P (x) dzieli się przez dwumian |x− α wtedy i tylko wtedy, gdy P (α) = 0.

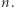
Twierdzenie 1 już zostało wykazane. Aby udowodnić twierdzenie 2, wystarczy zauważyć, że w wyrażeniu 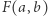F(a, b) wszystkie współczynniki są jednocześnie współczynnikami wielomianu 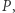P, więc są całkowite. Zatem wartość tego wyrażenia jest również liczbą całkowitą.

Kolej na dowód twierdzenia Bézouta. Niech 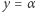y = α będzie stałą. Wtedy wyrażenie 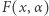F(x, α) jest wielomianem zmiennej 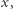x, a zapis 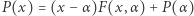|P(x) = (x− α)F(x, α) + P(α) jest dzieleniem wielomianu 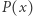P (x) przez dwumian 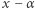|x− α z resztą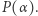 P(α ).

Uwaga. Jeśli wielomian 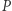P o współczynnikach całkowitych ma pierwiastek całkowity 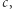|c, to wielomian 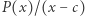P (x)/(x − c) również ma współczynniki całkowite.
Dowód pozostawiamy Czytelnikowi.