Klub 44M - zadania XII 2020»Zadanie 812
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2020
- Publikacja w Delcie: grudzień 2020
- Publikacja elektroniczna: 1 grudnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (421 KB)
-
Zadanie 812 zaproponował pan Tomasz Ordowski.
Udowodnić, że dla każdej liczby naturalnej 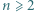 iloczyn
iloczyn 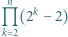 dzieli się przez
dzieli się przez 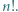
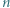
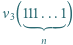
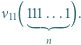
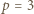 wystarczy rozważyć
wystarczy rozważyć 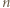 podzielne przez 3, a dla
podzielne przez 3, a dla 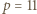 - rozważyć
- rozważyć  parzyste. Dla
parzyste. Dla 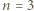 skorzystać z równości
skorzystać z równości 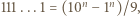 a dla
a dla 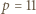 i
i 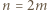 z równości
z równości 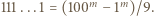
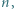
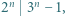
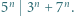
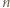 zachodzi nierówność
zachodzi nierówność 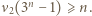 Wartość
Wartość 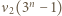 można wyznaczyć dokładnie, w zależności od parzystości
można wyznaczyć dokładnie, w zależności od parzystości 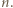 Skorzystać z nierówności
Skorzystać z nierówności 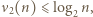 aby wykazać, że
aby wykazać, że 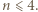
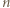 parzystych
parzystych 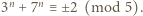 Dla
Dla 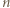 nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).
nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).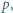
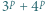
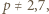 to
to 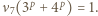
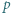 -adycznego w
-adycznego w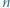
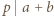 i
i 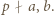 W przypadku
W przypadku 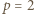 mamy
mamy 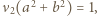 natomiast dla
natomiast dla 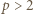 mamy
mamy 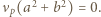
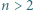
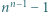
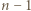 i stwierdzić, że
i stwierdzić, że 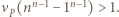

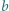
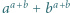
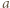 i
i 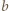 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 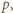 to
to 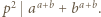 W przeciwnym razie istnieje liczba pierwsza
W przeciwnym razie istnieje liczba pierwsza 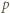 spełniająca warunki
spełniająca warunki 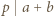 i
i 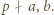 Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.
Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.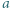
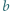
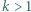
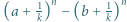
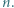
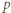 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 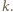 Jeśli liczba z zadania jest całkowita, to
Jeśli liczba z zadania jest całkowita, to 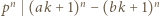 i można skorzystać z lematu, bo
i można skorzystać z lematu, bo 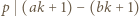 oraz
oraz 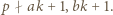
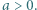
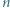
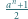
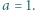
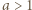 liczba
liczba 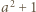 ma dzielnik pierwszy
ma dzielnik pierwszy 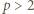 i dla odpowiednio dobranego nieparzystego
i dla odpowiednio dobranego nieparzystego 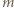 liczba
liczba 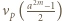 nie dzieli się przez 3.
nie dzieli się przez 3.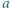
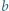
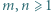
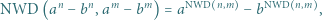
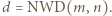 Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych
Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych 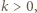 dla których
dla których 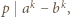 jest postaci
jest postaci 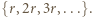
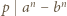 i
i 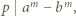 to
to 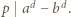
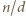 i
i 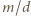
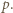 Wywnioskować z tego, że
Wywnioskować z tego, że 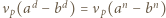 lub
lub 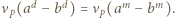
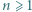
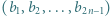
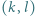
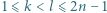
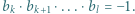
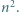
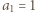
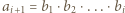
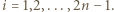
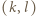
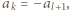
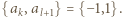
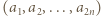
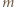
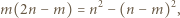
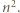
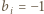
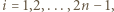
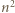
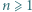
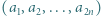
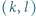
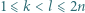
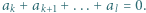
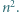
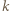
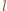
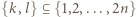
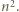
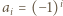
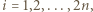
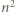
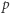 -adyczne
-adyczne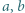
 :
:
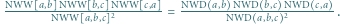
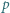
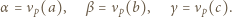
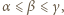
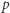 -adyczne
-adyczne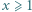
![|[x, 2x]](/math/temat/matematyka/teoria_liczb/zadania/2020/11/01/zm-20-11-kpo-2/2x-d7608384ddd380a3dd1f65eb0be5d8496d7a9363-im-2C,6B,73-FF,FF,FF.gif)
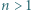 :
: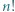
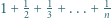
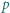
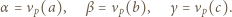
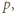
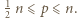
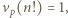
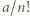
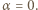
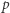 -adyczne
-adyczne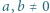
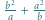
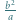
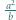
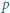
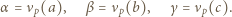
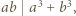
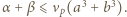
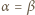
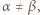
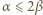
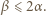
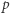 -adyczne
-adyczne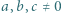
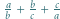
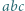
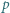
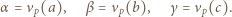
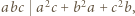
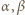
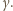
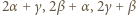
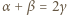
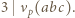
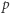 -adyczne
-adyczne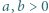
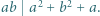

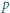
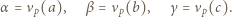
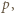
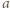
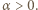

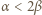
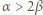
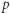 -adyczne
-adyczne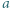
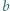
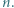
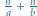
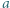
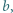
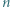
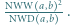
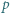
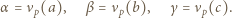
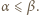
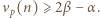
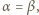
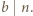
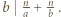
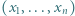
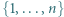
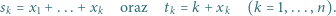
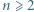
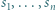

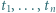
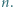
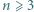 istnieją nieparzyste liczby
istnieją nieparzyste liczby 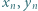 spełniające równanie
spełniające równanie 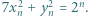
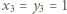 spełniają wymaganą w zadaniu równość. Załóżmy, że nieparzyste liczby
spełniają wymaganą w zadaniu równość. Załóżmy, że nieparzyste liczby 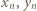 spełniają
spełniają 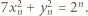 Wówczas
Wówczas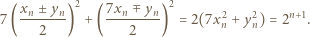
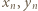 są nieparzyste, to jedna z par
są nieparzyste, to jedna z par 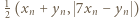 oraz
oraz 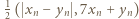 składa się z dwóch liczb nieparzystych, i tę parę wybieramy jako
składa się z dwóch liczb nieparzystych, i tę parę wybieramy jako 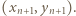 W ten indukcyjny sposób możemy skonstruować rozwiązanie wyjściowego równania dla dowolnej liczby naturalnej
W ten indukcyjny sposób możemy skonstruować rozwiązanie wyjściowego równania dla dowolnej liczby naturalnej 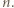
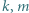 i zastępujemy je liczbami
i zastępujemy je liczbami 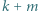 i
i 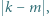 a trzecia liczba pozostaje bez zmiany. Z otrzymaną trójką postępujemy tak samo. Rozstrzygnąć, czy z każdej początkowej trójki liczb całkowitych nieujemnych można w ten sposób otrzymać trójkę, w której co najmniej dwie liczby są zerami.
a trzecia liczba pozostaje bez zmiany. Z otrzymaną trójką postępujemy tak samo. Rozstrzygnąć, czy z każdej początkowej trójki liczb całkowitych nieujemnych można w ten sposób otrzymać trójkę, w której co najmniej dwie liczby są zerami.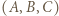 zapiszemy w postaci
zapiszemy w postaci 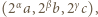 w której
w której 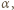
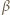 i
i 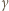 są całkowite nieujemne, zaś
są całkowite nieujemne, zaś 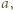
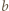 i
i  są nieparzyste lub równe 0. Jeśli w tej trójce jest najwyżej jedno zero, to stosując operacje z zadania, można doprowadzić do trójki
są nieparzyste lub równe 0. Jeśli w tej trójce jest najwyżej jedno zero, to stosując operacje z zadania, można doprowadzić do trójki 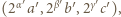 w której
w której 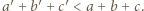 W tym celu przydatne są równości
W tym celu przydatne są równości 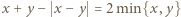 i
i 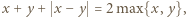 dzięki którym z trójki
dzięki którym z trójki 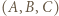 otrzymamy trójkę
otrzymamy trójkę 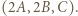
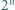 jedynek ma co najmniej
jedynek ma co najmniej 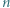 różnych dzielników pierwszych.
różnych dzielników pierwszych.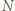 będzie liczbą składającą się w zapisie dziesiętnym z
będzie liczbą składającą się w zapisie dziesiętnym z 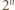 jedynek. Mamy
jedynek. Mamy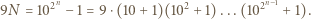
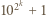 i
i 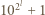 są względnie pierwsze dla
są względnie pierwsze dla 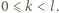 Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą
Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą 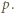 Oczywiście liczba
Oczywiście liczba 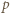 jest nieparzysta. Ponieważ
jest nieparzysta. Ponieważ 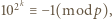 więc
więc 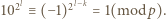 Skoro jednak
Skoro jednak 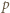 dzieli
dzieli 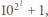 to
to 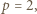 co przeczy wcześniej poczynionej uwadze o nieparzystości
co przeczy wcześniej poczynionej uwadze o nieparzystości 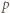 i kończy rozwiązanie zadania.
i kończy rozwiązanie zadania. taką, że liczby
taką, że liczby 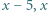 oraz
oraz 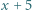 są kwadratami.
są kwadratami.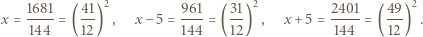
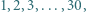 jeżeli podczas ważenia odważniki można układać tylko na jednej szalce.
jeżeli podczas ważenia odważniki można układać tylko na jednej szalce.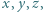 że
że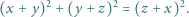
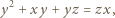
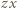 do obu stron daje
do obu stron daje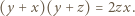
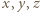 są nieparzyste, to lewa strona powyższej równości jest podzielna przez 4, w przeciwieństwie do prawej strony, co kończy rozwiązanie zadania.
są nieparzyste, to lewa strona powyższej równości jest podzielna przez 4, w przeciwieństwie do prawej strony, co kończy rozwiązanie zadania.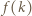 dla
dla 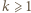 będzie liczbą liczb pierwszych w zbiorze
będzie liczbą liczb pierwszych w zbiorze 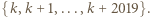 Wśród pierwszych 2020 liczb całkowitych dodatnich jest więcej niż 13 liczb pierwszych, zatem
Wśród pierwszych 2020 liczb całkowitych dodatnich jest więcej niż 13 liczb pierwszych, zatem 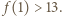 Zauważmy także, że wśród liczb
Zauważmy także, że wśród liczb 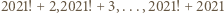 występują same liczby złożone, zatem
występują same liczby złożone, zatem 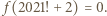 Oczywiście mamy
Oczywiście mamy 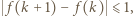 skąd wniosek, że istnieje taka liczba
skąd wniosek, że istnieje taka liczba 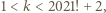 dla której mamy
dla której mamy 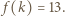 To kończy rozwiązanie zadania.
To kończy rozwiązanie zadania. będzie dowolną dodatnią liczbą nieparzystą. Spójrzmy na ciąg
będzie dowolną dodatnią liczbą nieparzystą. Spójrzmy na ciąg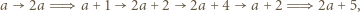
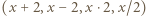 , zaś podwójna strzałka
, zaś podwójna strzałka 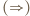 oznacza wielokrotne dodanie lub odjęcie dwójki, przebiegające monotonicznie przez wszystkie liczby tej samej parzystości, co liczby połączone tą podwójną strzałką. Na przykład dla
oznacza wielokrotne dodanie lub odjęcie dwójki, przebiegające monotonicznie przez wszystkie liczby tej samej parzystości, co liczby połączone tą podwójną strzałką. Na przykład dla 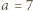 mamy ciąg
mamy ciąg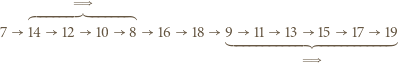
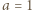 strzałka
strzałka 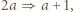 czyli
czyli 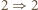 jest "pusta"). W tak określonym ciągu występują wszystkie liczby naturalne z przedziału
jest "pusta"). W tak określonym ciągu występują wszystkie liczby naturalne z przedziału ![|[a, 2a+ 5],](/math/temat/matematyka/teoria_liczb/zadania/2020/03/31/zm-k44-799/10x-22476a16ba6045895876a3c4680af4bf9c980bb5-im-66,57,43-FF,FF,FF.gif) każda jednorazowo.
każda jednorazowo.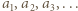 wzorem rekurencyjnym
wzorem rekurencyjnym 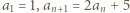 i zastosować podaną konstrukcję w każdym z przedziałów
i zastosować podaną konstrukcję w każdym z przedziałów ![[an,an+1].](/math/temat/matematyka/teoria_liczb/zadania/2020/03/31/zm-k44-799/3x-e1232ec1a01b8b6c5574063abc2b7eaab9e77fab-im-66,57,43-FF,FF,FF.gif)