Drobiazgi

Widoczność w nieskończonym lesie

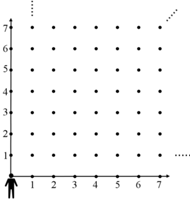
Stoimy u progu nieskończenie milowego, nad wyraz uporządkowanego lasu. Najlepszym miejscem na uporządkowany las jest oczywiście układ współrzędnych. Pnie drzew, które są odcinkami, umieszczone są w punktach o współrzędnych całkowitych nieujemnych. Nasz wzrok z punktu 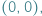$|(0;0);$ w którym drzewa nie ma, przygląda się temu zjawisku (patrz rysunek). Taki las ciągnie się nieskończenie daleko...

Kiedy patrzymy na drzewo 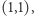$|(1,1),$ to zasłania ono wszystkie inne drzewa o współrzędnych 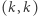$(k,k)$ (dla dowolnego 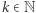$k ∈ N$ ). Podobnie drzewo 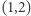$|(1,2)$ zasłania wszystkie drzewa o współrzędnych 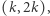$(k,2k),$ a drzewo 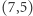$|(7,5)$ wszystkie drzewa o współrzędnych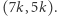 $|(7k,5k).$

Zadanie. Czy możliwe jest, aby z punktu 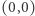$(0,0)$ spojrzeć na wskroś tego lasu, tak aby nie zobaczyć absolutnie żadnego drzewa?

Zauważmy, że spoglądając na drzewo 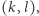$|(k,l),$ patrzymy wzdłuż prostej 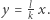$|y = lk x.$ Oznacza to, że spoglądając na dowolne drzewo, będziemy zawsze patrzeć wzdłuż prostej, której współczynnik kierunkowy jest liczbą wymierną. Aby nie mieć na linii wzroku żadnego drzewa, wystarczy spojrzeć w stronę punktu, którego dokładnie jedna współrzędna jest liczbą niewymierną.

Zadanie. Losujemy liczbę 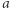$a$ z przedziału 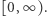$[0,∞ ).$ Jaka jest szansa, że patrząc wzdłuż prostej 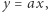$y = ax,$ zobaczymy drzewo?

Pytanie sprowadza się do zbadania, jaką część liczb rzeczywistych z przedziału 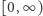$|[0, ∞ )$ stanowią liczby wymierne. Co z kolei prowadzi do stwierdzenia, że szansa na zobaczenie drzewa wynosi 0. Czytelnikom Niedowierzającym i tym, którzy dopiero rozpoczynają znajomość z przeliczalnością zbiorów, polecamy artykuł Joanny Jaszuńskiej w Delcie 7/2013.