Kącik początkującego olimpijczyka
Rachunki
Gauss, czyli tam i z powrotem
Według legendy pod koniec XVIII wieku działa się następująca rzecz. Pewien nauczyciel kazał swoim uczniom dodać wszystkie liczby od 1 do 40, aby mieć przez dłuższą chwilę spokój. Wszyscy, z wyjątkiem jednego, wykonywali pracowicie kolejne dodawania i zazwyczaj popełniali błędy...
Tym wyjątkowym uczniem był Carl Friedrich Gauss, który rozumował następująco:
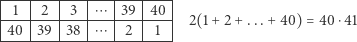 |
(lewą stronę równości otrzymujemy, sumując liczby w wierszach, a prawą - w kolumnach), więc 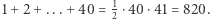 Podobne rozumowanie stosujemy w zadaniach 1-3. Idea jest taka, żeby parować składniki lub czynniki: najmniejszy z największym, drugi najmniejszy z drugim największym itd.
Podobne rozumowanie stosujemy w zadaniach 1-3. Idea jest taka, żeby parować składniki lub czynniki: najmniejszy z największym, drugi najmniejszy z drugim największym itd.
Powyższy trik można nieco uogólnić - przecież tabela może mieć więcej niż dwa wiersze, a parowanie najmniejszych z największymi też nie jest koniecznością.
Dla przykładu rozważmy ciąg liczbowy 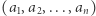 i niech
i niech 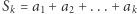 dla
dla 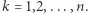 Wówczas
Wówczas
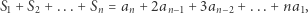 |
(1) |
co można wykazać za pomocą poniższej tabelki, po lewej stronie. Ta tożsamość rozwiązuje zadania 4 i 5.
 |
Podobne rozumowanie możemy stosować, zliczając wierszami i kolumnami pary liczb naturalnych spełniające określone warunki, gdyż każda taka para ma swoje miejsce w odpowiedniej tabeli.
Przykładowo policzmy wierszami i kolumnami pary 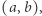 dla których
dla których 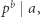 gdzie
gdzie 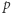 jest ustaloną liczbą pierwszą, zaś
jest ustaloną liczbą pierwszą, zaś 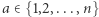 (w tabeli wyżej, po prawej:
(w tabeli wyżej, po prawej: 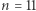 i
i 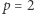 ). Pozostawimy Czytelnikowi zauważenie, że doprowadza to nas do twierdzenia Legendre'a: liczba pierwsza
). Pozostawimy Czytelnikowi zauważenie, że doprowadza to nas do twierdzenia Legendre'a: liczba pierwsza 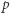 występuje w rozkładzie liczby
występuje w rozkładzie liczby 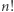 na czynniki pierwsze z wykładnikiem
na czynniki pierwsze z wykładnikiem
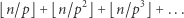 |
Takie podejście jest skuteczne w zadaniach 6 i 7.