Ogródek Gardnera
Rachunki
Co ma π do pierwiastków z dwóch i trzech?
Na początek krótka zagadka: co jest większe, 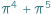 czy
czy 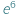 ? Drogi Czytelniku! Nie wysilaj się. Nie masz szans raczej tego poprawnie ocenić...
? Drogi Czytelniku! Nie wysilaj się. Nie masz szans raczej tego poprawnie ocenić...
Weź kalkulator i sprawdź: 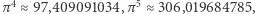 zaś
zaś 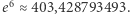 Suma tych pierwszych dwóch to
Suma tych pierwszych dwóch to 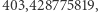 więc jest nieco mniejsza niż
więc jest nieco mniejsza niż 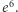 Różnica niewielka: ok.
Różnica niewielka: ok. 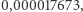 można powiedzieć, że niezauważalna. Błąd względny mniejszy od
można powiedzieć, że niezauważalna. Błąd względny mniejszy od 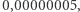 czyli od jednej dwudziestomilionowej. Gdybyśmy z taką precyzją chcieli podać wysokość Pałacu Kultury, to trzeba by go zmierzyć z dokładnością do około jednej setnej milimetra. Nie jest znane żadne wyjaśnienie, dlaczego te dwie liczby są tak bliskie. Wygląda to na czysty przypadek. Ile jeszcze takich zagadkowych zbiegów okoliczności mamy w matematyce?
czyli od jednej dwudziestomilionowej. Gdybyśmy z taką precyzją chcieli podać wysokość Pałacu Kultury, to trzeba by go zmierzyć z dokładnością do około jednej setnej milimetra. Nie jest znane żadne wyjaśnienie, dlaczego te dwie liczby są tak bliskie. Wygląda to na czysty przypadek. Ile jeszcze takich zagadkowych zbiegów okoliczności mamy w matematyce?
Krąży złośliwa anegdotka o tym, jak w amerykańskich szkołach pokazuje się niewymierność liczby 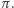 Ponieważ
Ponieważ 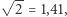 zaś
zaś 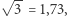 więc
więc 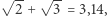 a to - jak wszyscy wiedzą - jest równe właśnie
a to - jak wszyscy wiedzą - jest równe właśnie 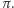 Również powszechnie wiadomo, że
Również powszechnie wiadomo, że 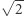 i
i 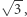 to liczby niewymierne, a że suma dwóch liczb niewymiernych jest niewymierna, więc i liczba
to liczby niewymierne, a że suma dwóch liczb niewymiernych jest niewymierna, więc i liczba 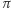 jest niewymierna.
jest niewymierna.
W tym "dowodzie" prawie każde stwierdzenie jest fałszywe. Czasami zadaję uczniom w szkole, aby wyszukali wszystkie błędy w tym sformułowaniu, prowadzącym do poprawnego skądinąd wniosku. Ciekawe natomiast jest to, że faktycznie 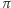 jest bardzo bliskie sumie tych dwóch jakże podstawowych pierwiastków. Znów przypadek?
jest bardzo bliskie sumie tych dwóch jakże podstawowych pierwiastków. Znów przypadek?

Nie do końca. Spójrzmy na rysunek. W czerwony sześciokąt foremny wpisane jest białe koło, a w to koło szary ośmiokąt foremny. Przyjmijmy, że promień koła wynosi 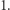 Pole koła jest nieco mniejsze niż pole sześciokąta, ale nieco większe niż pole ośmiokąta. Przy czym "na oko" różnice te są podobne: łączne pole wystających sześciu czerwonych prawie trójkątów i łączne pole ośmiu białych prawie trójkątów wyglądają dość podobnie. Innymi słowy pole koła jest mniej więcej średnią arytmetyczną pól tych wielokątów. Pozostaje zatem obliczyć pole sześciokąta foremnego opisanego na kole jednostkowym i pole ośmiokąta foremnego wpisanego w to koło i przekonać się, że pierwsze z nich to
Pole koła jest nieco mniejsze niż pole sześciokąta, ale nieco większe niż pole ośmiokąta. Przy czym "na oko" różnice te są podobne: łączne pole wystających sześciu czerwonych prawie trójkątów i łączne pole ośmiu białych prawie trójkątów wyglądają dość podobnie. Innymi słowy pole koła jest mniej więcej średnią arytmetyczną pól tych wielokątów. Pozostaje zatem obliczyć pole sześciokąta foremnego opisanego na kole jednostkowym i pole ośmiokąta foremnego wpisanego w to koło i przekonać się, że pierwsze z nich to 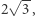 a drugie to
a drugie to 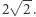 Ich średnia arytmetyczna to po prostu
Ich średnia arytmetyczna to po prostu 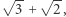 a że pole koła to
a że pole koła to 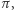 więc możemy zrozumieć, że w bliskości tych dwóch liczb nie ma większej tajemnicy.
więc możemy zrozumieć, że w bliskości tych dwóch liczb nie ma większej tajemnicy.
Czasem więc tego typu zagadkowa koincydencja ma racjonalne wytłumaczenie, tak jak to się stało na przykład w przypadku stałej Ramanujana
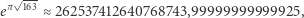 |
która jest tak bliska liczbie całkowitej, że Martin Gardner w numerze primaaprilisowym Scientific American z roku 1975 obwieścił po prostu, że to jest, zgodnie z przewidywaniami Ramanujana, liczba całkowita. Istniejące wtedy kalkulatory nie radziły sobie z taką dokładnością i łatwo było czytelników wkręcić w żart. Ramanujanowi się udało, bo jego imieniem nazwano stałą, która została dużo przed nim odkryta przez Charlesa Hermite'a (w 1859 r.), a on sam z nią akurat nie miał nic wspólnego. Ale żart Gardnera był na tyle nośny, że nazwisko słynnego Hindusa przylepiło się do tej stałej mocniej niż nazwisko prawdziwego odkrywcy. Okazuje się, że bliskość tego wyrażenia do liczby całkowitej bynajmniej przypadkowa nie jest, lecz wynika z algebraicznej teorii pierścieni i związanych z nimi liczb Heegnera.