Konstrukcja trójkąta Sierpińskiego została podana przez Wacława Sierpińskiego w 1915 roku, choć już wcześniej obserwowano mozaiki i inne wzory o podobnym kształcie. Ten fraktal powstaje w następujący sposób: dowolny trójkąt (u Sierpińskiego równoboczny) dzielony jest na cztery mniejsze identyczne trójkąty, z których środkowy jest usuwany; na pozostałych trzech trójkątach cały proces dzielenia i usuwania środkowej części powtarza się w nieskończoność. Powstała "na końcu" figura to właśnie trójkąt Sierpińskiego. Na rysunku poniżej przedstawionych jest pierwszych sześć etapów konstrukcji, gdy początkowy trójkąt jest równoboczny.

Trójkąt Sierpińskiego ma wiele zaskakujących związków z innymi obiektami matematycznymi, takimi jak trójkąt Pascala, gra w chaos, L-systemy, iterowane systemy funkcji czy popularna łamigłówka "Wieże Hanoi". My przedstawimy jego związek z grą w życie.

Gra w życie jest algorytmem opisanym następującymi regułami:

• gra rozgrywa się na nieskończonej płaskiej planszy, podzielonej na identyczne kwadratowe komórki; w szczególności każda komórka sąsiaduje z ośmioma komórkami dokoła niej,
• każda komórka znajduje się w jednym z dwóch stanów: jest albo żywa, albo martwa,
• gra odbywa się w turach (układ ewoluuje); w każdej turze tworzony jest nowy układ (generacja) komórek na podstawie poprzedniej tury,
• gdy martwa komórka uzyska dokładnie trzech żywych sąsiadów, staje się żywa w kolejnej generacji - tak powstaje nowe życie,
• żywa komórka posiadająca dokładnie dwóch lub trzech sąsiadów przeżywa do następnej generacji; w przeciwnym razie staje się martwa.

Powyższe reguły pozwalają na tworzenie ogromnej liczby bardzo ciekawych wzorów. Na rysunku poniżej przedstawiony jest prosty przebieg gry dla układu trzech żywych komórek (oznaczone czarnym kolorem).

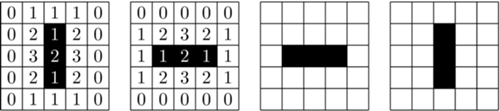
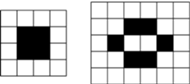
Liczby w kwadratach oznaczają liczbę żywych sąsiadów danej komórki. W tym przykładzie generacje ewoluują okresowo - czyli w którejś z tur powtarza się układ, który wystąpił już wcześniej. Generacja jest zaś stała, gdy w kolejnych ewolucjach układy żywych i martwych komórek są identyczne (rysunki na marginesie).

Gra w życie jest szczególnym przypadkiem automatu komórkowego - przykładem ogromnej klasy algorytmów komputerowych, które zostały również sformalizowane w języku matematyki.

Bogactwo różnych schematów, układów okresowych i wielu obrazów wygenerowanych w grze w życie sprawia, że mający prawie pół wieku algorytm nadal jest popularny (istnieje choćby cała grupa ludzi, którzy tworzą coraz ciekawsze konstrukcje z użyciem współczesnych programów symulujących grę - jednym z takich programów jest golly, dostępny w internecie na stronie golly.sourceforge.net) i nie zaszkodziły słowa Johna Conwaya - twórca gry wielokrotnie przyznawał, że nie lubi własnego pomysłu.

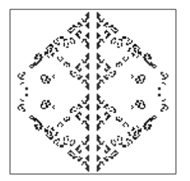
Co łączy trójkąt Sierpińskiego z grą w życie? Otóż ten fraktal można wygenerować w grze Conwaya. Ściślej - nie sam fraktal, a jedynie jego zarys, który oddaje przybliżoną strukturę jednego z etapów jego konstrukcji. Tę strukturę można otrzymać, gdy początkowym stanem będzie długa "kreska" (czyli długi rząd żywych komórek). Wtedy pewna generacja takiego układu będzie przypominać fraktal.

Spójrzmy na przykład po prawej stronie. Nie jest oczywiste, że rysunek odzwierciedla fraktal (a w istocie - dwie jego kopie zestawione podstawami) - wzór powstał z generacji złożonej ze 130 komórek ustawionych w linii poziomej i jest efektem 65 ewolucji. Duże odstępstwo od właściwego kształtu, szczególnie w okolicy prawego i lewego końca rysunku, wynika z małej skali generacji początkowej (mało żywych komórek).

Dużo lepsze rezultaty otrzymamy, gdy stanem początkowym będzie kilka-kilkadziesiąt tysięcy komórek ustawionych w jednej linii. Film pokazuje, że "wystarczy" około 15000 komórek, aby otrzymać wyraźny obraz fraktala. Własne eksperymenty można prowadzić również we wspomnianym wcześniej programie golly.

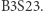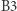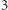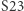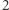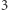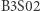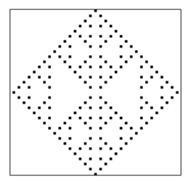
Reguły gry Conwaya można modyfikować według uznania. Klasyczne zasady zmiany stanu komórek (opisane wcześniej) oznacza się przez Zapis interpretujemy następująco: oznacza warunek rodzenia się nowej komórki (rodzi się, gdy ma dokładnie żywych sąsiadów; is born); to warunek przeżywalności ( lub żywych sąsiadów gwarantuje przeżycie; survives). Zastosujmy inną regułę do stanu początkowego 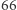żywych komórek ułożonych w linii prostej. Efekt takiej gry okazuje się odzwierciedlać trójkąt Sierpińskiego w stopniu znacznie dokładniejszym niż reguła 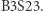Rysunek obok przedstawia efekt po kilkudziesięciu generacjach, który jest jednocześnie stanem stałym - każda kolejna generacja jest identyczna z tą widoczną na rysunku.

Niezwykłe jest powiązanie dwóch odległych od siebie obiektów w matematyce. Dostrzeżenie takiego powiązania jest wspaniałym doświadczeniem. Jest nim niewątpliwie połączenie fraktali z automatami komórkowymi. Trójkąt Sierpińskiego może więc grać w życie - i to dosłownie. Przetrwa bowiem jako generacja ewoluująca okresowo (w regule 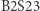) albo jako generacja stała (reguła ).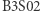