Dodając obustronnie 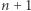do równości 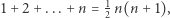dowodzimy implikacji

Zwróćmy uwagę, że druga równość jest analogiczna do pierwszej, z tą jedynie różnicą, że każde zostało zastąpione przez 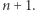To tłumaczy nazwy 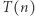i 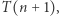które zostały tym równościom nadane.

Zauważmy, że 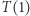jest równością prawdziwą: 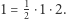Wyżej udowodniona implikacja dla 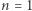ma postać 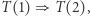zatem i równość 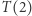jest prawdziwa. Następnie biorąc 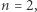wnioskujemy prawdziwość 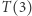i tak dalej, przez cały zbiór liczb naturalnych. To oznacza, że 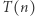jest zdaniem prawdziwym dla każdego naturalnego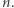

Powyższe rozumowanie jest przykładem dowodu przez indukcję. Ogólniej, zasada indukcji matematycznej mówi, że jeśli chcemy wykazać prawdziwość jakiegoś stwierdzenia 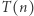dla wszystkich liczb naturalnych 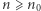(zwykle 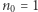), to wystarczy udowodnić 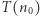(baza indukcji), a następnie dla wszystkich naturalnych 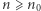dowieść, że 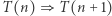(krok indukcji; stwierdzenie 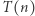nazywamy tu założeniem indukcyjnym, a 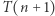- tezą indukcyjną).

Przedstawiamy poniżej jeszcze dwa rodzaje indukcji. Indukcję o głębokości 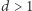stosujemy w zadaniach 3 i 8, a silną indukcję w zadaniach 9 i 10.

Indukcja o głębokości 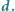Bazę indukcji stanowią stwierdzenia 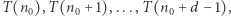a w kroku indukcyjnym dowodzimy implikacji 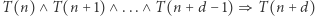dla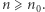

Silna indukcja. Bazą jest stwierdzenie 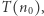a krokiem indukcyjnym 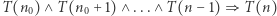dla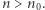

Zadania. (Uwaga. Przyjmujemy, że 0 nie jest liczbą naturalną.)