Co to jest?
Drobiazgi
Relacje
Mając dane dwa zbiory 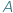 i
i 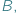 relacją zdefiniowaną pomiędzy tymi dwoma zbiorami matematycy nazywają po prostu podzbiór zbioru wszystkich par elementów, w których pierwszy jest ze zbioru
relacją zdefiniowaną pomiędzy tymi dwoma zbiorami matematycy nazywają po prostu podzbiór zbioru wszystkich par elementów, w których pierwszy jest ze zbioru 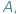 a drugi ze zbioru
a drugi ze zbioru 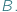 Inaczej mówiąc, element ze zbioru
Inaczej mówiąc, element ze zbioru 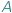 i element ze zbioru
i element ze zbioru 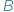 mogą być w danej relacji lub w niej nie być.
mogą być w danej relacji lub w niej nie być.
Relacje często występują na świecie, np. posiadanie psa jest relacją pomiędzy zbiorem wszystkich ludzi a zbiorem wszystkich psów. Człowiek o imieniu Dionizy jest w tej relacji z psem Dingiem wtedy i tylko wtedy, gdy Dingo jest jego pupilem.
Szczególnie interesujące wydają się relacje zdefiniowane na jednym zbiorze, czyli gdy 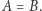 Na przykład relacja
Na przykład relacja 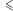 zdefiniowana na liczbach rzeczywistych. Liczba
zdefiniowana na liczbach rzeczywistych. Liczba 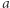 jest w relacji
jest w relacji 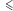 z liczbą
z liczbą 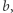 jeśli
jeśli  nie jest większe od
nie jest większe od 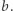 Innym przykładem jest relacja koloru zdefiniowana na zbiorze wszystkich samochodów, gdzie dwa samochody są w tej relacji, jeśli są tego samego koloru. Jeszcze inny przykład to relacja małżeństwo zdefiniowana na zbiorze wszystkich ludzi.
Innym przykładem jest relacja koloru zdefiniowana na zbiorze wszystkich samochodów, gdzie dwa samochody są w tej relacji, jeśli są tego samego koloru. Jeszcze inny przykład to relacja małżeństwo zdefiniowana na zbiorze wszystkich ludzi.
Można badać cechy poszczególnych relacji. Powiemy, że dana relacja jest zwrotna, jeśli każdy element jest w relacji z samym sobą. Z wyżej wymienionych przykładów relacja 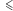 oraz relacja koloru mają tę cechę (ale małżeństwo już nie). Relacja jest symetryczna, jeśli z tego, że element
oraz relacja koloru mają tę cechę (ale małżeństwo już nie). Relacja jest symetryczna, jeśli z tego, że element 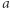 jest w relacji z elementem
jest w relacji z elementem 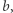 wynika, że element
wynika, że element 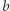 jest w relacji z elementem
jest w relacji z elementem 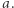 Widzimy, że relacja koloru oraz małżeństwo są przykładami takich relacji, zaś relacja
Widzimy, że relacja koloru oraz małżeństwo są przykładami takich relacji, zaś relacja 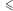 nie jest. I w końcu, relacja jest przechodnia, jeśli z tego, że
nie jest. I w końcu, relacja jest przechodnia, jeśli z tego, że 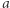 jest w relacji z
jest w relacji z 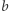 i
i 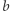 jest w relacji z
jest w relacji z 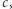 wynika, że
wynika, że 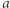 jest w relacji z
jest w relacji z 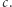 Jasne jest, że
Jasne jest, że 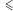 oraz relacja tego samego koloru są przykładami tego typu relacji.
oraz relacja tego samego koloru są przykładami tego typu relacji.
Relacja, która jest równocześnie zwrotna, symetryczna i przechodnia, nazywana jest relacją równoważności. Taka właśnie jest relacja koloru. Takie relacje mają wyjątkową cechę: generują podział danego zbioru na rozłączne podzbiory, których każde dwa elementy są w relacji. W wypadku relacji koloru jest to podział wszystkich samochodów na zbiory samochodów w poszczególnych kolorach: żółte, czerwone, niebieskie itd. Tak utworzone podzbiory matematycy nazywają klasami abstrakcji. Zauważmy również, że każdy podział rozważanego zbioru generuje na nim relację równoważności, w której dwa elementy są w relacji, o ile znajdują się w tej samej części podziału. Tę równoważność pomiędzy relacjami równoważności i podziałami matematycy nazywają zasadą abstrakcji.