Kraty
Na płaszczyźnie euklidesowej  zbiór
zbiór 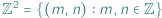 nazywamy kratą, a jego elementy punktami kratowymi.
nazywamy kratą, a jego elementy punktami kratowymi.
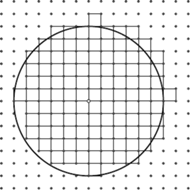
Rys. 1. Liczba  jest równa powierzchni pokrytej przez kwadraty jednostkowe, których dolny lewy wierzchołek leży wewnątrz lub na brzegu koła.
jest równa powierzchni pokrytej przez kwadraty jednostkowe, których dolny lewy wierzchołek leży wewnątrz lub na brzegu koła.
Carl Gauss zauważył, że jeśli liczba punktów kratowych w kole 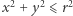 wynosi
wynosi  to
to 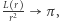 gdy
gdy 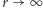 (Rys. 1). Empirycznie wyznaczył
(Rys. 1). Empirycznie wyznaczył 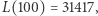 więc
więc 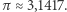 Precyzyjnie, Gauss pokazał, że
Precyzyjnie, Gauss pokazał, że 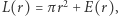 gdzie błąd
gdzie błąd 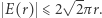 Do dziś nie wiemy, jakie jest najlepsze oszacowanie tego błędu.
Do dziś nie wiemy, jakie jest najlepsze oszacowanie tego błędu.

Rys. 2. 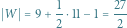
Szybko okazało się, że kraty to ciekawy obiekt badań matematycznych. Na przykład, na płaszczyźnie łatwo wykreślić prostą, która nie przecina zbioru 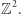 Jeśli na prostej znajdują się dwa punkty kratowe, to jest ich na tej prostej nieskończenie wiele i są one rozmieszczone w równych odstępach. Istnieją też proste, które zawierają dokładnie jeden punkt kratowy. Gdyby prosta przechodząca przez punkty
Jeśli na prostej znajdują się dwa punkty kratowe, to jest ich na tej prostej nieskończenie wiele i są one rozmieszczone w równych odstępach. Istnieją też proste, które zawierają dokładnie jeden punkt kratowy. Gdyby prosta przechodząca przez punkty  i
i 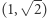 zawierała punkt kratowy
zawierała punkt kratowy 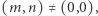 to z twierdzenia Talesa uzyskalibyśmy, że
to z twierdzenia Talesa uzyskalibyśmy, że 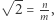 a to jest niemożliwe, bo
a to jest niemożliwe, bo 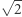 jest liczbą niewymierną.
jest liczbą niewymierną.
Analizując pola wielokątów o wierzchołkach w punktach kraty 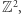 Georg Pick wykazał niespodziewanie, że wiedza o liczbie i położeniu punktów kratowych w wielokącie określa jego pole.
Georg Pick wykazał niespodziewanie, że wiedza o liczbie i położeniu punktów kratowych w wielokącie określa jego pole.
Twierdzenie 1 (G. Pick, 1899). Pole wielokąta 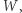 którego wierzchołki są punktami kraty
którego wierzchołki są punktami kraty 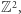 a boki nie przecinają się, jest równe
a boki nie przecinają się, jest równe
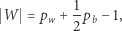
gdzie 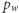 i
i 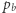 oznaczają, odpowiednio, liczbę punktów kratowych we wnętrzu i na brzegu wielokąta (Rys. 2).
oznaczają, odpowiednio, liczbę punktów kratowych we wnętrzu i na brzegu wielokąta (Rys. 2).
Jednym z istotniejszych wyników o punktach kratowych jest rezultat Hansa Blichfeldta:
Twierdzenie 3 (H. Blichfeldt, 1914). Dla dowolnej liczby naturalnej 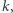 dowolny zbiór ograniczony
dowolny zbiór ograniczony 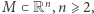 o objętości większej od
o objętości większej od 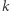 można tak przesunąć, by zawierał co najmniej
można tak przesunąć, by zawierał co najmniej 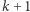 elementów kraty
elementów kraty 
Część I. Problem i rozwiązanie
W 1957 r. Hugo Steinhaus w Matematyce 10 (2), str. 58-59, przedstawił kilka zadań konkursowych dotyczących kraty 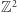 :
:
Zadanie (A). Udowodnić, że dla każdej liczby naturalnej  istnieje koło, zawierające wewnątrz dokładnie
istnieje koło, zawierające wewnątrz dokładnie  punktów kratowych.
punktów kratowych.
Zadanie (B). Znaleźć największe koło zawierające wewnątrz dokładnie: (a) 0 punktów kratowych, (b) 1 punkt kratowy, (c) 2 punkty kratowe, (d) 3 punkty kratowe, (e) 4 punkty kratowe, (f) 5 punktów kratowych. Podać średnice tych kół.
Zadanie (C). Największe koło zawierające wewnątrz dokładnie 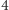 punkty kratowe można tak przesunąć, żeby wewnątrz miało dokładnie
punkty kratowe można tak przesunąć, żeby wewnątrz miało dokładnie 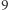 punktów kratowych, a także dokładnie
punktów kratowych, a także dokładnie 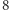 lub
lub 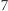 punktów kartowych. Czy można je tak przesunąć, żeby w jego wnętrzu było dokładnie
punktów kartowych. Czy można je tak przesunąć, żeby w jego wnętrzu było dokładnie 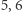 lub
lub 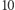 punktów kratowych?
punktów kratowych?
Rozwiązania Steinhausa znajdzie Czytelnik w książce Jeszcze 105 zadań Hugona Steinhausa opracowanej przez Edwarda Piegata, Oficyna Wydawnicza GiS, Wrocław 2000.
Rozwiązanie Zadania A podał też Wacław Sierpiński w czasopiśmie L'Enseignement Mathématique (2) 4 (1958), str. 25-31. Pomysł Sierpińskiego opierał się na następującej obserwacji:
każde dwa różne punkty kraty
mają różne odległości od punktu
tj. nie ma okręgu o tym środku przechodzącego przez dwa lub więcej punktów kraty.

Istotnie, niech 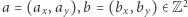 i
i  Jeżeli
Jeżeli 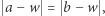 to
to
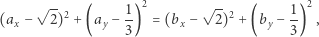
czyli
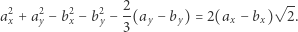
Prawa strona jest więc liczbą wymierną, zatem 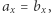 ale wówczas
ale wówczas
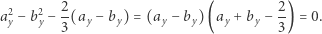
Jest to możliwe jedynie, gdy 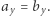 Zatem
Zatem 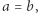 sprzeczność.
sprzeczność.
Rozwiązanie Sierpińskiego. Krata 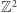 jest zbiorem przeliczalnym, więc korzystając z powyższej obserwacji, wszystkie jej elementy możemy ustawić w ciąg
jest zbiorem przeliczalnym, więc korzystając z powyższej obserwacji, wszystkie jej elementy możemy ustawić w ciąg 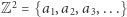 tak, że
tak, że
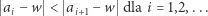
Wówczas koło otwarte
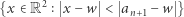
zawiera wszystkie punkty kratowe 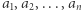 i żadnych innych. Voilà!
i żadnych innych. Voilà!
Mamy więc:
Twierdzenie 4. Dla każdej liczby naturalnej  istnieje koło o środku
istnieje koło o środku  którego wnętrze zawiera dokładnie
którego wnętrze zawiera dokładnie  punktów kratowych.
punktów kratowych.
Podobne rozumowanie (szczegóły pozostawiamy Czytelnikom) pokazuje, że dla każdej liczby naturalnej 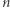 istnieje kula o środku w punkcie
istnieje kula o środku w punkcie 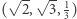 zawierająca wewnątrz dokładnie
zawierająca wewnątrz dokładnie 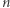 punktów kraty
punktów kraty 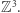
Część II. Pokłosie
Naturalne jest pytanie o istnienie okręgów przechodzących dokładnie przez  punktów kraty
punktów kraty  Łatwo rysujemy okręgi przechodzące przez
Łatwo rysujemy okręgi przechodzące przez 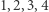 punkty kratowe. A jak jest dla większej liczby punktów kratowych?
punkty kratowe. A jak jest dla większej liczby punktów kratowych?
W 1958 r. Andrzej Schinzel, korzystając z twierdzenia teorii liczb:
Twierdzenie. Liczba 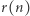 rozwiązań równania
rozwiązań równania 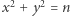 w liczbach całkowitych (= ilość rozkładów liczby naturalnej
w liczbach całkowitych (= ilość rozkładów liczby naturalnej 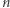 na sumę kwadratów dwóch liczb całkowitych) jest równa
na sumę kwadratów dwóch liczb całkowitych) jest równa 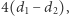 gdzie
gdzie 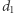 jest liczbą dzielników liczby
jest liczbą dzielników liczby  postaci
postaci 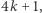 a
a  jest liczbą dzielników liczby
jest liczbą dzielników liczby  postaci
postaci 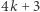
(dowód w tym numerze, w artykule Michała Krycha),
udowodnił:
Twierdzenie 5 (A. Schinzel, 1958). Dla każdej liczby naturalnej  na okręgu opisanym równaniem
na okręgu opisanym równaniem
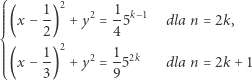 |
leży dokładnie 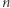 punktów kraty
punktów kraty 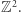
Korzystając z rezultatu Schinzla, Tadeusz Kulikowski wykazał:
Twierdzenie 6 (T. Kulikowski, 1959). Dla każdej liczby naturalnej  istnieje sfera, która zawiera dokładnie
istnieje sfera, która zawiera dokładnie  punktów kraty
punktów kraty 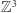 .
.
Dowód. Ustalmy 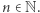 Z twierdzenia Schinzla na płaszczyźnie
Z twierdzenia Schinzla na płaszczyźnie  istnieje okrąg
istnieje okrąg  na którym leży dokładnie
na którym leży dokładnie 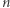 punktów
punktów 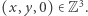 Rozważmy sferę o środku w punkcie
Rozważmy sferę o środku w punkcie  i promieniu
i promieniu 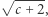 gdzie
gdzie 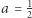 lub
lub 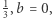 a
a  to kwadrat odpowiedniego promienia z twierdzenia 4:
to kwadrat odpowiedniego promienia z twierdzenia 4:
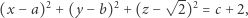 |
(*) |
skąd

Liczby całkowite 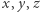 mogą spełniać to równanie tylko wtedy, gdy
mogą spełniać to równanie tylko wtedy, gdy 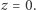 Oznacza to, że wszystkie punkty
Oznacza to, że wszystkie punkty 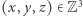 leżące na sferze
leżące na sferze 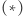 leżą na przecięciu tej sfery z płaszczyzną
leżą na przecięciu tej sfery z płaszczyzną 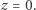 Zatem jedyne punkty kratowe na sferze
Zatem jedyne punkty kratowe na sferze 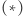 to
to 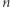 punktów kratowych należących do okręgu Schinzla.
punktów kratowych należących do okręgu Schinzla.
W tym samym czasie Jerzy Browkin zauważył, że funkcja
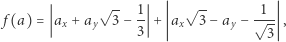
(gdzie 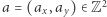 ) przyjmuje różne wartości dla każdych dwóch różnych punktów kraty
) przyjmuje różne wartości dla każdych dwóch różnych punktów kraty 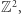 oraz dowiódł, że dla każdej liczby naturalnej
oraz dowiódł, że dla każdej liczby naturalnej 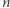 :
:
- istnieje kwadrat zawierający wewnątrz (odpowiednio: na brzegu) dokładnie
 punktów kraty
punktów kraty 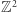 ,
, - istnieje sześcian zawierający wewnątrz dokładnie
 punktów kraty
punktów kraty 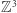 .
.
Podobne problemy można rozważać dla figur o innych kształtach - trójkątów, elips. Oczywiście największe zainteresowanie budzą problemy, które mimo wysiłków nadal pozostają bez odpowiedzi.
Problem 1. Czy istnieje prostopadłościan, którego krawędzie, przekątne ścian, przekątna wewnętrzna mają długości całkowite?
Historia tego problemu sięga 1719 roku, gdy Paul Halcke wskazał prostopadłościan 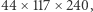 którego przekątne ścian też są całkowitej długości.
którego przekątne ścian też są całkowitej długości.
Problem 2 (H. Steinhaus). Czy istnieje taki podzbiór 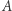 płaszczyzny, że każdy zbiór przystający do
płaszczyzny, że każdy zbiór przystający do 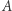 zawiera dokładnie jeden punkt kratowy?
zawiera dokładnie jeden punkt kratowy?
Spacer po kracie 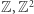 lub
lub 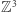 polegający na tym, że w każdym kolejnym kroku przechodzimy o jedną jednostkę do sąsiedniego punktu kratowego (mając równe szanse poruszania się w każdym możliwym kierunku) nazywamy symetrycznym błądzeniem przypadkowym. George Pólya pokazał w 1921 roku, że w przypadku takiego błądzenia w kracie
polegający na tym, że w każdym kolejnym kroku przechodzimy o jedną jednostkę do sąsiedniego punktu kratowego (mając równe szanse poruszania się w każdym możliwym kierunku) nazywamy symetrycznym błądzeniem przypadkowym. George Pólya pokazał w 1921 roku, że w przypadku takiego błądzenia w kracie 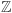 lub
lub 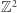 z prawdopodobieństwem równym
z prawdopodobieństwem równym  powrócimy do położenia początkowego. W kracie
powrócimy do położenia początkowego. W kracie 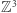 prawdopodobieństwo to wynosi około
prawdopodobieństwo to wynosi około  Tak więc naprawdę zabłądzić możemy w kratach
Tak więc naprawdę zabłądzić możemy w kratach  gdzie
gdzie 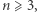 ale to temat na inne spotkanie.
ale to temat na inne spotkanie.
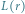 jest równa powierzchni pokrytej przez kwadraty jednostkowe, których dolny lewy wierzchołek leży wewnątrz lub na brzegu koła.
jest równa powierzchni pokrytej przez kwadraty jednostkowe, których dolny lewy wierzchołek leży wewnątrz lub na brzegu koła.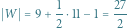
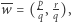 to punkty kratowe
to punkty kratowe 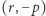 i
i 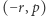 są tak samo odległe od punktu
są tak samo odległe od punktu 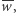 gdyż
gdyż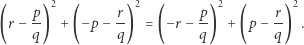
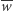 jest
jest 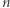 punktów kratowych, to żadne koło o środku w punkcie
punktów kratowych, to żadne koło o środku w punkcie 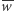 nie zawiera
nie zawiera  punktów kratowych.
punktów kratowych.