Deltoid

Kolorowa płaszczyzna

Większości problemów otwartych współczesnej matematyki nie da się zrozumieć bez zaawansowanej wiedzy, ale zdarzają się też takie, których sformułowania są zupełnie elementarne. Poniższa seria zadań prowadzi do jednego z nich.

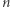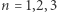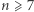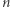Podsumowując, jeśli każdy punkt płaszczyzny pomalowano jednym z $|n$ kolorów, to dla $n = 1,2,3$ muszą istnieć dwa punkty odległe o 1 i tego samego koloru, dla $n ⩾ 7$ nie muszą i jeśli dla pewnego $n$ nie muszą, to dla większych $n$ też nie muszą. Liczba chromatyczna płaszczyzny 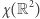$χ (R2)$ to najmniejsza wartość 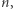$n,$ dla której rozważane punkty nie muszą istnieć; powyżej uzasadniliśmy, że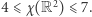 $|4⩽ χ(R2) ⩽ 7.$

Dokładna wartość 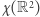$2 χ (R )$ nie jest znana, jest to tzw. problem Hadwigera-Nelsona. Sformułowanie i powyższe rezultaty pochodzą z lat 1950-60 i do niedawna nic więcej nie było wiadomo. W kwietniu 2018 roku Aubrey de Grey opublikował w internecie pracę [AdG], w której udowodnił, że 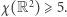$2 χ(R )⩾ 5.$ Skonstruował graf o 1581 wierzchołkach i 7877 krawędziach długości 1 i pokazał (wspomagając się komputerem), że nie da się pomalować jego wierzchołków czterema kolorami bez krawędzi o jednobarwnych końcach. Dowód ten szybko sprawdzono, a następnie w ramach internetowego projektu Polymath 16 [P16] ruszyły zbiorowe poszukiwania mniejszego grafu o tej własności (najlepiej nie wymagającego komputera do badania go). We wrześniu 2018 roku najmniejszy znany taki graf miał 553 wierzchołki i 2722 krawędzie.