Stowarzyszenie na rzecz Edukacji Matematycznej
LXVI Olimpiada Matematyczna

W LXVI Olimpiadzie Matematycznej uczestniczyło 895 uczniów, więc aż o 272 osoby mniej niż rok wcześniej, do zawodów stopnia drugiego zakwalifikowano 409 uczniów, a do zawodów stopnia trzeciego -126 uczniów. Wiele osób, w tym niżej podpisany, uznało, że zadania domowe były za trudne i nie zachęcały uczniów spoza szkół o dużych tradycjach olimpijskich (a raczej uczniów nauczycieli, którzy uczą matematyki, a nie tylko przygotowują do zdania matury) do startowania w tych zawodach.
Niektóre okręgi obniżyły zwyczajowe progi dopuszczenia do zawodów drugiego stopnia, ale i tak zakwalifikowano do nich o 98 osób mniej niż rok wcześniej. Komisja zadaniowa OM starała się wziąć pod uwagę te czynniki. Jako członek tego gremium uznaję, że zadania na zawody drugiego i trzeciego stopnia nie były za trudne.
Do finału dopuściliśmy tych uczniów, którzy uzyskali co najmniej 19 punktów, co oznacza rozwiązanie 3,5 zadania (np. 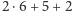 ). Obniżenie progu do 18 punktów oznaczałoby dopuszczenie dodatkowych 22 osób do finału.
). Obniżenie progu do 18 punktów oznaczałoby dopuszczenie dodatkowych 22 osób do finału.
Zadania finałowe dobrze rozróżniły czołówkę: tym razem ustalając składy reprezentacji Polski na Olimpiadę Międzynarodową i inne zawody, nie musieliśmy korzystać z wyników zawodów okręgowych. Tylko 9 finalistów (około 7%) nie rozwiązało żadnego zadania (w drugim stopniu było to 30 osób (około 7,4%)).
Najtrudniejsze z zadań finałowych było zadanie piąte, z planimetrii, choć spodziewaliśmy się, że będzie nim zadanie trzecie, z kombinatoryki. Co więcej, w czasie omawiania rozwiązań tuż po zawodach dwóch byłych olimpijczyków przedstawiło swe rozwiązania tego zadania wykorzystujące wiele twierdzeń, często nieznanych większości słuchających.
Oto treść zadania:
Zadanie. Dowieść, że przekątne wypukłego czworokąta są prostopadłe wtedy i tylko wtedy, gdy wewnątrz tego czworokąta znajduje się punkt, którego rzuty prostokątne na boki czworokąta są wierzchołkami prostokąta.
Podam jego "antygeometryczne" rozwiązanie. Drobne luki Czytelnicy wypełnią, jeśli zechcą, sami.
Załóżmy, że rzuty punktu 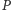 na boki czworokąta
na boki czworokąta 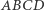 tworzą prostokąt i obierzmy układ współrzędnych tak, by
tworzą prostokąt i obierzmy układ współrzędnych tak, by 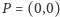 był jego początkiem, a osie były równoległe, odpowiednio, do boków prostokąta. Niech rzutem
był jego początkiem, a osie były równoległe, odpowiednio, do boków prostokąta. Niech rzutem 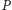 na
na 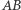 będzie punkt
będzie punkt 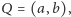 na bok
na bok 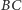 - punkt
- punkt 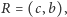 na bok
na bok 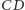 - punkt
- punkt 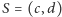 a na bok
a na bok 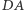 - punkt
- punkt 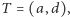 przy czym
przy czym 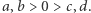 Prosta
Prosta 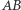 jest prostopadła do wektora
jest prostopadła do wektora 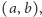 więc ma równanie
więc ma równanie 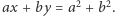 Podobnie równaniami prostych
Podobnie równaniami prostych 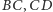 i
i 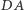 są odpowiednio
są odpowiednio 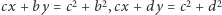 i
i 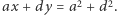
Proste 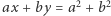 i
i 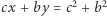 przecinają się w punkcie
przecinają się w punkcie 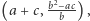 więc
więc 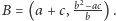 Podobnie
Podobnie 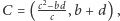
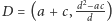 i
i 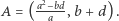 Prosta
Prosta 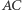 jest równoległa do osi
jest równoległa do osi 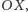 a prosta
a prosta 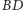 - do osi
- do osi 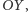 więc przekątne prostokąta
więc przekątne prostokąta 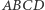 są prostopadłe.
są prostopadłe.
Z kolei gdy czworokąt  ma prostopadłe przekątne, możemy umieścić go tak, by miał wierzchołki na osiach:
ma prostopadłe przekątne, możemy umieścić go tak, by miał wierzchołki na osiach: 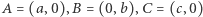 i
i  Z już udowodnionego wiemy, że jeśli rzuty pewnego punktu tworzą prostokąt, ma on boki równoległe do osi. Równaniem prostej
Z już udowodnionego wiemy, że jeśli rzuty pewnego punktu tworzą prostokąt, ma on boki równoległe do osi. Równaniem prostej 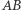 jest
jest 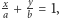 bo spełniają je współrzędne punktów
bo spełniają je współrzędne punktów 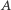 i
i 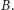 Analogicznie równaniami prostych
Analogicznie równaniami prostych 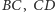 i
i 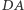 są odpowiednio
są odpowiednio 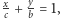
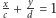 i
i 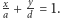 Niech
Niech
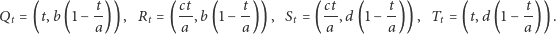
Wyliczone zostały kolejno współrzędne tych punktów w zależności od pierwszej współrzędnej punktu 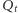 oznaczonej literą
oznaczonej literą 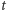 tak, by punkt
tak, by punkt 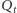 leżał na prostej
leżał na prostej 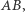 punkt
punkt 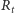 - na
- na 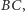 punkt
punkt 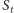 - na
- na 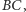 punkt
punkt 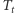 - na
- na 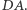 Znajdziemy taki punkt
Znajdziemy taki punkt 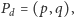 że odcinek
że odcinek 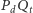 będzie prostopadły do prostej
będzie prostopadły do prostej 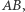 a odcinek
a odcinek 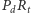 - prostopadły do prostej
- prostopadły do prostej 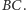 Spełnione mają być równości
Spełnione mają być równości
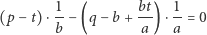
oraz
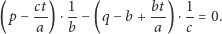
Wynika z nich, że 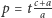 i
i 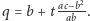 W taki sam sposób znajdujemy taki punkt
W taki sam sposób znajdujemy taki punkt 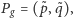 że
że 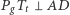 i
i 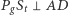 :
:
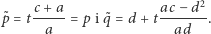
Obliczymy 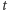 z równania
z równania 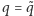 :
:
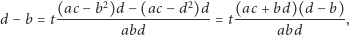
zatem 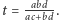 Dla tego
Dla tego 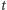 otrzymujemy
otrzymujemy
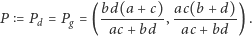
Rzutami punktu 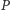 na proste
na proste 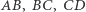 i
i 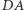 są punkty
są punkty
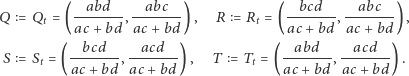
Jedyną trudnością w tym rozwiązaniu jest wybranie "dobrego" układu współrzędnych.