Rozprawka o metodzie

Na początek stwierdzenie: w nauce, a zwłaszcza w matematyce, zajmujemy się tylko wyjątkowymi, wyidealizowanymi sytuacjami.

A może lepiej zacząć tak: do tego, o co nam chodzi, co nas interesuje, dorobiliśmy sobie taki świat, taką całość, że to, od czego zaczęliśmy, stało się wyjątkowe.

Ponieważ może się to wydawać mętne i wątpliwe, więc przyjrzyjmy się przykładom.

Przykład 1. Liczby będące wynikiem pomiarów wszystkie są wymierne, a więc wyjątkowe, zaniedbywalne wśród - uważanych przez nas za zwyczajne - liczb rzeczywistych.

Przykład 2. Na powierzchnie patrzymy tak, że wydają się nam niesłychanie regularne. Tak doskonałe, by można było stwierdzić, że

(Jacob Bernoulli) krzywizna normalna powierzchni ma dwa ekstrema i to w kierunkach prostopadłych;
(Leonhard Euler) krzywiznę każdej krzywej normalnej opisuje równość 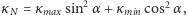$|κN =κ max sin2α + κmincos2α,$ gdzie kąt 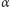$α$ mierzymy od kierunku minimalnej krzywizny.
(Jean Meusnier) krzywiznę dowolnej krzywej na powierzchni opisuje równość 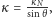$|κ= -κN , sinθ$ gdzie krzywa normalna i dana mają wspólną styczną, a 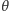$θ$ to kąt między płaszczyzną ściśle styczną do krzywej i płaszczyzną styczną do powierzchni.

Przykład 3. Nawet geometrię obraliśmy tak,

by w niej grupy izometrii, podobieństw i przekształceń afinicznych to były trzy różne grupy;
by wśród geometrii riemannowskich o stałej krzywiźnie stanowiła ona wspólny brzeg bogactwa geometrii hiperbolicznych i eliptycznych;
co więcej: by jedynie nasza (szkolna, euklidesowa) płaszczyzna - spośród wszystkich jednorodnych geometrii o wymiarze większym od 1 - nie dopuszczała paradoksalnego rozkładu, czyli by jej grupa izometrii nie miała podgrup wolnych.

Zamiast mnożyć przykłady postawmy pytanie:

czy możliwa jest matematyka nietraktująca rzeczywistych sytuacji za wyjątki, czyli niedolepiająca do tego, co naprawdę jest, absurdalnych dodatków w rodzaju liczb przestępnych, ciągłych funkcji $[0,1]$ na $|[0,1]$ w żadnym przedziale niemonotonicznych, paradoksalnych rozkładów czy indukcji pozaskończonej itp.?

A odpowiedź jest TAK. Co więcej, większość czasu, w którym ludzie zajmowali się liczbami i figurami, wypełniona była taką matematyką.

Cały artykuł dostępny jest w wersji do druku [application/pdf]: (104 KB)