Olimpiada Matematyczna Gimnazjalistów (OMG), młodsza siostra Olimpiady Matematycznej, powstała w roku 2005 dzięki zapałowi i pasji ludzi związanych z Komitetem Głównym Olimpiady Matematycznej. W regulaminie OMG wpisano: Celem zawodów Olimpiady Matematycznej Gimnazjalistów jest rozbudzanie zamiłowania do matematyki wśród młodzieży szkół gimnazjalnych, wyszukiwanie uczniów zainteresowanych matematyką, kształtowanie umiejętności samodzielnego zdobywania wiedzy oraz stymulowanie aktywności poznawczej młodzieży uzdolnionej.

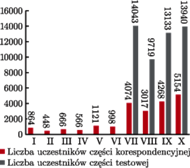
Wykres obok przedstawia liczbę uczniów startujących w kolejnych edycjach Olimpiady. Gwałtowny wzrost liczby uczestników od VII OMG spowodowany jest rozszerzeniem pierwotnej formuły o część testową.

Zapisany w regulaminie cel "rozbudzania zamiłowania do matematyki..." realizowany jest nie tylko przez organizację zawodów, ale też przez różne działania towarzyszące, skierowane do uczniów (gazetka Kwadrat, Facebokowa Liga Zadaniowa, obozy naukowe) oraz nauczycieli (seminaria i wydawnictwa).

Organizatorzy pierwszej olimpiady swoją pasją zarazili innych. W organizację olimpiady włącza się czynnie duża grupa wolontariuszy, w większości finalistów i laureatów poprzednich edycji. Oni też pracują obecnie w Komitecie Głównym, Komitetach Okręgowych i Komisji Zadaniowej.

W czasie zawodów finałowych X OMG uczestnicy mieli, jak zwykle, trzy godziny na rozwiązanie pięciu zadań. Najtrudniejsze okazało się zadanie, które przytaczam poniżej. Tylko kilku zawodników przedstawiło poprawne rozwiązanie tego zadania.

Zadania, w których pojawia się pytanie o istnienie wielościanu spełniającego określone warunki, występują często wśród zadań olimpijskich. W dziesięciu edycjach olimpiady, na różnych etapach znajdziemy 10 zadań tego typu. Zawsze należało uzasadnić, że odpowiednią bryłę można zbudować. Konstrukcja wielościanu o zadanych własnościach wymagała od uczestników sporej wyobraźni i pomysłowości.

Czasem, aby skonstruować wielościan o wymaganych własnościach, trzeba dokładnie przyjrzeć się znanym bryłom i zauważyć tam pewne prawidłowości.

Często aby skonstruować wielościan o pewnych własnościach, trzeba "zdeformować" inny "regularny" wielościan, na przykład, poprzez wycięcie lub doklejenie jakiegoś elementu.

I jeszcze zadanie do samodzielnego rozwiązania.

Czytelnik Uważny znajdzie wielościan o żądanych własnościach wśród prezentowanych w tym artykule. Proponujemy znalezienie innych przykładów.