Deltoid
Oszacujmy pole
Korzystając z tytułowego pomysłu oraz z rysunku lub drobnych jego modyfikacji, można udowodnić szereg twierdzeń z różnych działów matematyki.


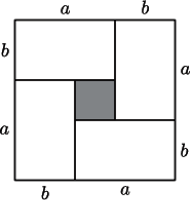
- Zauważmy, że pole całego kwadratu jest nie mniejsze od sumy pól czterech zawartych w nim białych prostokątów. Stąd
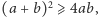 uzyskujemy więc
uzyskujemy więc 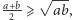 czyli nierówność pomiędzy średnią arytmetyczną a geometryczną.
czyli nierówność pomiędzy średnią arytmetyczną a geometryczną. - Dla
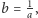 każdy z prostokątów ma pole równe 1, zatem
każdy z prostokątów ma pole równe 1, zatem 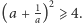 Stąd liczba dodatnia i jej odwrotność zawsze dają w sumie co najmniej 2.
Stąd liczba dodatnia i jej odwrotność zawsze dają w sumie co najmniej 2. - Zamiast kwadratu o boku
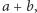 rozważmy kwadrat o boku
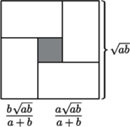
rozważmy kwadrat o boku 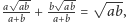 przedstawiony na rysunku 2. Analogiczna jak dotychczas analiza pól pozwala udowodnić nierówność pomiędzy średnią geometryczną a harmoniczną:
przedstawiony na rysunku 2. Analogiczna jak dotychczas analiza pól pozwala udowodnić nierówność pomiędzy średnią geometryczną a harmoniczną: 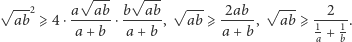
- Ciąg Fibonacciego definiujemy tak:
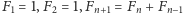 dla
dla 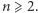 Rozumowanie podobne do powyższych pozwala dowieść następującej tożsamości:
Rozumowanie podobne do powyższych pozwala dowieść następującej tożsamości: 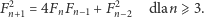
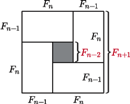
Rozważmy w tym celu kwadrat o boku
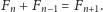 Zauważmy, że mały szary kwadracik pośrodku ma wówczas bok długości
Zauważmy, że mały szary kwadracik pośrodku ma wówczas bok długości 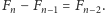 Wobec tego powyższa tożsamość opisuje pole całego dużego kwadratu.
Wobec tego powyższa tożsamość opisuje pole całego dużego kwadratu. - Podobnie, analiza objętości sześcianu o krawędzi
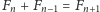 podzielonego na kilka części tak, jak na rysunku, pozwala dowieść tożsamości
podzielonego na kilka części tak, jak na rysunku, pozwala dowieść tożsamości 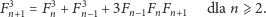
- Z rysunku obok można dla odmiany odczytać, że dla nieparzystych liczb naturalnych
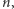 liczba
liczba 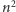 daje przy dzieleniu przez 8 resztę 1.
daje przy dzieleniu przez 8 resztę 1.
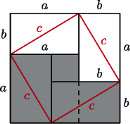
- Oznaczmy przekątne prostokątów z pierwszego rysunku przez
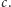 Usuwając cztery "zewnętrzne" trójkąty, otrzymujemy kolorowy kwadrat o boku
Usuwając cztery "zewnętrzne" trójkąty, otrzymujemy kolorowy kwadrat o boku 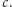 Z kolei usuwając cztery "górne" trójkąty, uzyskujemy szarą figurę złożoną z kwadratów o bokach
Z kolei usuwając cztery "górne" trójkąty, uzyskujemy szarą figurę złożoną z kwadratów o bokach  i
i 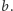 Równość pól prowadzi do twierdzenia Pitagorasa:
Równość pól prowadzi do twierdzenia Pitagorasa: 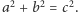
Ponadto, co najmniej połowa kwadratu jest szara, czyli
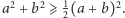 Stąd nierówność pomiędzy średnią kwadratową a arytmetyczną:
Stąd nierówność pomiędzy średnią kwadratową a arytmetyczną: 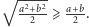
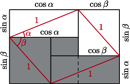
- Przekątne prostokątów z ostatniego rysunku mają długości
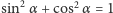 oraz
oraz 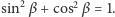 Dwukrotnie usuwając po cztery trójkąty prostokątne, podobnie jak powyżej, uzyskujemy z jednej strony kolorowy romb o boku 1 i kącie
Dwukrotnie usuwając po cztery trójkąty prostokątne, podobnie jak powyżej, uzyskujemy z jednej strony kolorowy romb o boku 1 i kącie 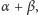 z drugiej zaś strony szarą figurę złożoną z dwóch prostokątów. Stąd równość pól:
z drugiej zaś strony szarą figurę złożoną z dwóch prostokątów. Stąd równość pól: 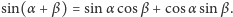
Warto poszukać na pierwszym rysunku dowodów innych ciekawych faktów oraz odpowiedzi na pytanie, kiedy w opisanych powyżej nierównościach zachodzą równości.