Mięśnie, które je kontrolują, mają bowiem wpływ również na ruch głowy - możesz to sprawdzić, próbując kręcić głową z maksymalnie zaciśniętymi szczękami, a następnie próbując zrobić to samo ze szczękami rozluźnionymi, obserwując jednocześnie, w którym przypadku ruch jest łatwiejszy i płynniejszy. Ten sam eksperyment można powtórzyć w celu zbadania relacji ruchu głowy i oczu: spróbuj pokręcić swobodnie głową, trzymając oczy utkwione w jednym punkcie na ścianie. Ponieważ przemieszczenie głowy jest dla naszego układu nerwowego zadaniem priorytetowym, nawet gdy natrafia na pewne utrudnienie (na przykład zbyt mocno zaciśnięte szczęki), znajdzie on sposób, żeby to zadanie wykonać. Często jest to jednak sposób nieoptymalny i odbywający się kosztem innych partii ciała, które muszą wówczas pracować dużo ciężej. W podobny sposób ból pleców może być skojarzony ze sposobem, w jaki używamy naszych stóp, ból kolana czy biodra może zależeć od organizacji barku, a ból w barku może mieć dużo wspólnego z brakiem mobilności w biodrze. W tego typu problemach właściwie niemożliwe jest wyróżnienie jednej przyczyny czy źródła problemu, nawet jeżeli ból odczuwamy tylko w konkretnym miejscu. Istotna jest organizacja ruchu naszego ciała jako jednej całości. Być może tłumaczy to w pewnym stopniu ogromną nieskuteczność służb zdrowia w walce z dolegliwościami kręgosłupa - w samych Stanach Zjednoczonych wydaje się na ten cel ponad 100 miliardów dolarów rocznie. Ponieważ większa część tych pieniędzy przeznaczona jest na zakup lekarstw, których zadaniem jest tylko i wyłącznie stłumienie bólu, a nie rozwiązanie prawdziwego problemu, efektów nie widać.

Prawdopodobnie zaczęliście się w tym momencie zastanawiać, czy na pewno trzymacie w ręce kolejny numer Delty, czy może jednak przypadkiem sięgnęliście po miesięcznik przeznaczony dla fizjoterapeutów. Cały ten rozwlekły wstęp ma na celu przedstawienie pewnego fenomenu, który można zaobserwować w wielu innych dziedzinach życia i nauki, z matematyką włącznie. Chodzi o sytuację, w której rozważana przez nas dziedzina funkcjonuje bardziej jako jedna całość niż jako suma swoich odrębnych części. Zamierzeniem tego, jak i następnych artykułów, jest ukazanie bardziej holistycznego spojrzenia na matematykę, przez zwrócenie uwagi na często zaskakujące i głębokie związki między różnymi jej obszarami.

O tym, jak owo holistyczne spojrzenie jest istotne, wie każdy, kto choć trochę interesuje się postępem współczesnej matematyki. Praktycznie wszystkie największe odkrycia ostatnich lat są bowiem wynikiem genialnego połączenia różnych jej dziedzin. Być może najbardziej narzucającym się przykładem jest wielkie twierdzenie Fermata: dla liczby naturalnej 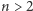nie istnieją liczby naturalne 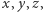które spełniałyby równanie 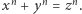Chociaż sformułowanie tego twierdzenia powinno być w pełni zrozumiałe dla uczniów szkoły podstawowej, to jego dowód (na który przyszło czekać ponad 300 lat) jest w rzeczywistości konsekwencją bardzo głębokiego wyniku z dziedziny krzywych eliptycznych. Potrzeba było jednak wiele czasu, żeby znaleźć związek pomiędzy trudną i bardzo abstrakcyjną teorią tych krzywych a wyjątkowo konkretnym i wręcz narzucającym się pytaniem dotyczącym liczb całkowitych.

Za inny przykład może posłużyć twierdzenie Greena i Tao udowodnione przez nich w 2004 roku. Głosi ono, że w ciągu wszystkich liczb pierwszych znajdują się dowolnie długie ciągi arytmetyczne. Chociaż podobnie jak w poprzednim przykładzie zagadnienie jest pozornie o czysto teorioliczbowym charakterze, to jego dowód jest osadzony głęboko w realiach teorii ergodycznej, korzystający jednocześnie w istotny sposób z analizy harmonicznej, geometrii dyskretnej i metody probabilistycznej. Również dowód słynnej hipotezy Poincarégo, jedynego rozwiązanego do tej pory problemu milenijnego, opiera się na badaniu tzw. potoków Ricciego, zaawansowanego pojęcia geometrii różniczkowej. W dziedzinie kombinatoryki ekstremalnej bardzo dużą popularnością cieszą się obecnie tzw. algebry flagowe, które pochodzą ze świata algebry wyższej. Tego typu przykłady można by wymieniać bardzo długo.

Naszym celem nie jest jednak dokładna analiza powyższych rezultatów, gdyż przekroczyłaby ona znacznie zarówno objętość Delty, jak i kompetencje autora. To, co jednak leży w naszym zasięgu, to zademonstrowanie podobnego fenomenu na dużo mniej doniosłych (lecz często równie fascynujących) przykładach. Bardzo często również w matematyce elementarnej można bowiem napotkać zupełnie zaskakujące dowody, które ujawniają związki między pozornie istotnie różnymi koncepcjami.

Zademonstrujemy to zjawisko na przykładzie zadań o charakterze olimpijskim. W artykule pokażemy parę różnorodnych, niezwiązanych ze sobą przykładów. W kolejnych omówimy bardziej szczegółowo wybrane metody, które ukazują głęboko położone relacje. Należy w tym momencie zaznaczyć, że nad każdym z omawianych dalej przykładów warto zastanowić się przez dłuższą chwilę samodzielnie przed sięgnięciem do rozwiązania. W innym przypadku łatwo bowiem przegapić prawdziwą trudność zadania i nie wychwycić subtelnego pomysłu, który pozwala ją pokonać.

Zaczniemy od, być może, dobrze znanego przykładu z dziedziny geometrii płaskiej.

Powyższy przykład, chociaż stosunkowo nietrudny i z całą pewnością doskonale znany specjalistom, dobrze ilustruje opisywany przez nas fenomen - treść zadania dotyczyła okręgu wpisanego, ale to będący w cieniu okrąg dopisany odegrał kluczową rolę w rozwiązaniu.

Drugi przykład demonstruje, jak przydatne może być znalezienie pewnej zewnętrznej struktury, którą w naturalny sposób można dopasować do rozważanego przez nas problemu. Czytelnik jest gorąco zachęcany do próby odnalezienia jej najpierw samodzielnie.

Kolejna ilustracja pochodzi z Międzynarodowej Olimpiady Matematycznej. Tym razem do rozwiązania klasycznego zadania z teorii liczb użyjemy twierdzeń cosinusów i Ptolemeusza z planimetrii!

W ostatnim z zadań zaprezentujemy zaskakujące zastosowanie algebry w zagadnieniu z geometrii kombinatorycznej, dotyczącym punktów i prostych na płaszczyźnie. Wykorzystamy dobrze znany fakt: jednorodny układ liniowy o mniejszej liczbie równań niż niewiadomych ma nietrywialne rozwiązanie. Jak zawsze, zachęcamy do próby samodzielnego rozwiązania - nawet z tą podpowiedzią nie będzie to wcale takie proste!

Na zakończenie zaproponujemy dwa zadania, dla których Czytelnik może sam spróbować odnaleźć zaskakujący sposób rozwiązania.

W kolejnych artykułach przedyskutujemy znacznie dokładniej wybrane metody, ukazujące niezwykłe związki w matematyce.