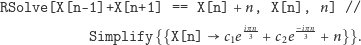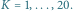Systemy algebry komputerowej

We współczesnym świecie komputery mają coraz większy wpływ zarówno na sposób uprawiania matematyki, jak i na samą matematykę. Wielu ważnych problemów, zarówno czysto teoretycznych, jak i pochodzących z zastosowań, nie można rozwiązać bez pomocy odpowiednich programów. Umiejętność posługiwania się komputerem w obliczeniach numerycznych i symbolicznych należy dziś do podstawowego wykształcenia matematyka.

Zwykle najbardziej efektywne jest użycie programów zaprojektowanych specjalnie do takich obliczeń, często nazywanych CAS (Computer Algebra System – system algebry komputerowej). Są to np. Macsyma, Maple, Maxima, MuPad, MatLab, Reduce, Axiom, Magma, Macaulay, Singular, i wiele innych – wśród nich znajdują się zarówno programy komercyjne, jak i darmowe oraz open source. Te programy mają zaimplementowane najnowsze algorytmy z różnych dziedzin matematyki, a także udostępniają języki programowania pozwalające użytkownikowi na pisanie własnych programów. Odgrywają wielką rolę w powstawaniu nowego działu nauki zwanego matematyką eksperymentalną.

Można wyróżnić dwa typy systemów algebry komputerowej: programy wyspecjalizowane w szczególnych działach matematyki (np. algebra przemienna, teoria grup, numeryczna algebra liniowa, równania różniczkowe, statystyka itd.), oraz programy ogólne, służące „do wszystkiego”. Chcemy tu przedstawić program Mathematica [1], należący do tej drugiej grupy. Jest on bardzo wszechstronny, a jednocześnie różne jego funkcje dobrze współdziałają. Spróbujemy pokazać zakres możliwości zastosowania Mathematiki na przykładzie automatów komórkowych. Jest to zagadnienie, w którym bez programu komputerowego byłoby bardzo trudno otrzymać ciekawe wyniki. Ponadto nie tylko leży w obrębie matematyki eksperymentalnej, ale jest także blisko związane z historią Mathematiki oraz z osobą jej pomysłodawcy. Mathematica jest, oczywiście, dziełem wielu osób – nikt nie byłby w stanie napisać samodzielnie tak dużego, a przede wszystkim wszechstronnego programu. Jednak główna idea i istotna część implementacji są dziełem jednej osoby: fizyka Stephena Wolframa.

Wolfram i jego dzieło

Wolfram, urodzony w 1959 r., jest niezwykłą i wybitną, choć także kontrowersyjną, postacią. Swój pierwszy artykuł opublikował, mając 18 lat, jako student fizyki na uniwersytecie w Oxfordzie (gdzie został przyjęty w wieku 15 lat). Opuścił uniwersytet, formalnie nie ukończywszy studiów, jako autor dziewięciu artykułów. Uzyskał stopień doktora na Uniwersytecie Caltech w Los Angeles, gdzie został zatrudniony. Był jedną z pierwszych osób, której przyznano słynny „grant dla geniuszy” (MacArthur Fellowship). Będąc w Caltech, Wolfram współtworzył system algebry komputerowej SMP, który stał się później podstawą Mathematiki.

W 1983 r. w Institute for Advanced Study w Princeton Wolfram rozpoczął badania automatów komórkowych, które stały się głównym obiektem jego zainteresowań naukowych. Podstawową metodę stanowiły symulacje komputerowe, a pierwsze wersje Mathematiki były ich głównym narzędziem. W 1987 r. Wolfram stworzył firmę Wolfram Research, zajmującą się głównie rozwojem i marketingiem Mathematiki i innych powiązanych z nią programów. Rok później opuścił świat akademicki, poświęcając się całkowicie prowadzeniu firmy oraz badaniom dotyczącym automatów komórkowych. W dalszej części tekstu przyjrzymy się obiektom tych badań i możliwościom, które przy pracy nad tym zagadnieniem daje Mathematica.

Automaty komórkowe

Pojęcie automatu komórkowego zostało wprowadzone przez Johna von Neumanna i Stanisława Ulama w celu modelowania samoreprodukcji wyidealizowanych systemów biologicznych. Nadaje się ono jednak równie dobrze do modelowania dyskretnych systemów fizycznych lub chemicznych. Takie systemy można uważać za przybliżenia układów dynamicznych, czyli systemów modelowanych za pomocą równań różniczkowych.

Rys. 1 Dziewięć generacji dwuwymiarowego automatu komórkowego Gra w życie.

Automat komórkowy składa się z dyskretnej siatki komórek w  -wymiarowej przestrzeni. Każda komórka może przyjmować skończoną liczbę stanów. System ewoluuje z pewnej konfiguracji początkowej, czas jest liczony dyskretnie. Nowy stan każdej komórki zależy od jej otoczenia w poprzedniej chwili. Jest kilka naturalnych definicji otoczenia, ale najczęściej przyjmuje się, że składa się ono z rozważanej komórki i wszystkich z nią sąsiadujących. Stan wszystkich komórek zmienia się równocześnie, tworząc nową generację.

Najbardziej popularny przykład, dwuwymiarowy, to wymyślona przez Johna Conwaya Gra w życie. W grze Conwaya komórki przyjmują dwa stany: są żywe lub martwe. Martwa komórka, która ma dokładnie trzech żywych sąsiadów, staje się żywa w następnej jednostce czasu (rodzi się), żywa komórka z dwoma albo trzema żywymi sąsiadami pozostaje nadal żywa, natomiast przy innej liczbie sąsiadów umiera (z samotności albo zatłoczenia).

Automaty w Mathematice

Wolfram przywiązuje wielką wagę do badań złożonych systemów za pomocą automatów komórkowych, określił to nawet jako „nowy rodzaj nauki” – część wspomnianej wcześniej matematyki eksperymentalnej. Zatem trudno się dziwić, że w Mathematice istnieje funkcja CellularAutomaton. Na przykład kod tworzący rysunku 1 wygląda tak:

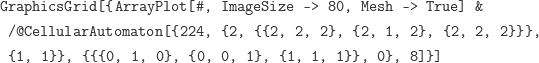
By wyjaśnić działanie tej funkcji (a także uzyskać pewne pojęcie o języku Mathematiki), posłużymy się bardzo prostym przykładem automatu: jednowymiarowym z tylko dwoma stanami, które będziemy oznaczali cyframi 1 i 0. Za otoczenie danej komórki będziemy przyjmowali tę komórkę wraz z dwiema sąsiednimi. Takie automaty Wolfram nazywa elementarnymi. Reguła ewolucji takiego automatu może być zapisana w języku Mathematiki na wiele różnych sposobów. Najczęściej używana jest metoda Wolframa, która przedstawia regułę ewolucji w postaci liczby.

W przypadku elementarnego automatu musimy zapisać, jak w kolejnym kroku ewolucji zmienia się środkowa cyfra w każdej z 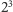  możliwych trójek 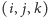 złożonych z zer i jedynek. To jest równoważne podaniu jednej liczby ośmiocyfrowej zapisanej w systemie dwójkowym (lub jej dziesiętnego równoważnika). Kolejne cyfry (dwójkowe) tej liczby mówią, na co zmieni się środkowy element w kolejnych trójkach ustawionych w ciąg malejący liczb w systemie dwójkowym. Na przykład reguła 30, czyli binarnie 00011110, oznacza automat, w którym

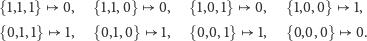
Dla automatów w wyższych wymiarach można zastosować podobny zapis. W najprostszej formie funkcja CellularAutomaton ma trzy argumenty: liczbę oznaczającą regułę (w przykładzie z rysunku 1 jest to 224), stan początkowy i liczbę kroków ewolucji.

Automat – generator liczb pseudolosowych

Rys. 2

Rys. 3 Etap ewolucji trójwymiarowego automatu nr 14

Rysunek 2 prezentuje początkowe sto generacji rozwoju automatu komórkowego opisywanego przez regułę 30. Na tym automacie oparty jest jeden z generatorów liczb pseudolosowych używanych przez Mathematicę. Ewolucję tego automatu można też opisać za pomocą formuły rekurencyjnej

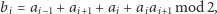gdzie 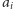 oznacza 0 (biały piksel) lub 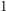(czarny piksel) w kolumnie 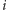 pewnego wiersza a 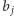  w kolumnie 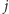 następnego. Stan początkowy określony jest w kodzie przez 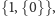 co oznacza jedynkę otoczoną nieskończonymi ciągami zer (jak widać w pierwszym wierszu). Okazuje się, że wartości w środkowej kolumnie zachowują się losowo. Otrzymujemy w ten sposób generator liczb pseudolosowych, który bardzo dobrze się sprawdza, mimo że oparty jest na prostej i oczywiście deterministycznej formule. Jak widać, nie tylko rozwój Mathematiki służy badaniu automatów komórkowych, ale zachodzi również zależność odwrotna.

Oczywiście, ten automat można dosyć łatwo zaprojektować i przedstawić graficznie właściwie w dowolnym języku programowania, ale w Mathematice cały kod tworzący rysunek 2 to tylko jedna linijka:

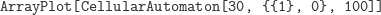Dla bardziej złożonych automatów komórkowych wcale nie jest dużo trudniej. Ponadto, za pomocą graficznych bibliotek Mathematiki można stworzyć wiele spektakularnych ilustracji ewolucji automatów komórkowych – jedną z nich pokazuje rysunek 3

Automaty i równania różniczkowe

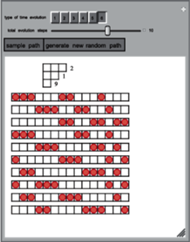
Rys. 4 Przykład solitonowego automatu komórkowego (Reiko Sakamoto, źródło: strona internetowa Wolfram Demonstrations Project,

Jak wspomnieliśmy, automaty komórkowe mogą być rozważane jako skrajne przykłady dyskretyzacji równań różniczkowych, gdzie nie tylko czas i przestrzeń są dyskretne, ale także rozwiązanie istnieje tylko w skończonym zbiorze możliwych stanów. Okazuje się, że większość zjawisk opisywanych przy użyciu teorii równań różniczkowych ma swoje odpowiedniki w teorii automatów komórkowych. Między innymi istnieją odpowiedniki tzw. solitonów (pewnych fal o ciekawych własnościach), które od wielu lat intrygują badaczy. Symulację solitonu, autorstwa Reiko Sakamoto, widzimy na rysunku 4 Przy okazji, przykład ten pokazuje tzw. dynamikę, czyli rodzaj interaktywności, będący jedną z najciekawszych cech Mathematiki od wersji 6 włącznie.

Automaty (i uogólnienia), które można badać (prawie) bez komputera

Wprawdzie automaty komórkowe bardzo trudno badać metodami matematycznymi – jest niewiele nietrywialnych twierdzeń – ale, jak widzieliśmy, doskonale nadają się do symulacji komputerowych. Istnieją także automaty komórkowe, nazywane całkowalnymi, dla których można otrzymać pewne wyniki za pomocą metod matematyczno-fizycznych. Właśnie takim automatem jest ten na rysunku 4 Ostatnio duże zainteresowanie budzą uogólnienia automatów komórkowych nazywane równaniami ultradyskretnymi (ang. ultra discrete equations), mające własność całkowalności. Powstają one z równań dyskretnych przez pewne przejście graniczne.

Rys. 5 Rozwiązania równania (2) dla

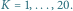
Rozważmy, na przykład, równanie dyskretne

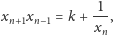(1)

gdzie 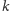 jest stałą. Ponieważ

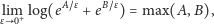więc wprowadzając nowe zmienne 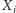 zdefiniowane wzorem 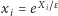 i przechodząc do granicy przy 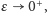 uzyskujemy równanie ultradyskretne

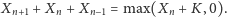(2)

Dla stałej 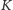 i początkowych wartośc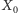i  i 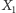  będących liczbami całkowitymi wszystkie rozwiązania tego równania są całkowite. Można wykazać, że przy iteracjach równania (1) nie zmienia się następująca wielkość:

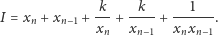Odpowiadający jej niezmiennik dla równania (2) to

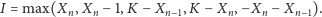Więcej na ten temat można znaleźć w artykule [2]. Wprawdzie Mathematica nie jest w stanie znaleźć ogólnego rozwiązania tych równań, ale za to możemy łatwo zilustrować rozwiązania graficznie w przestrzeni 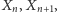 np. z wartościami początkowymi 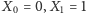 dla 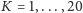 (zob. Rys. 5).

Ogólnie szukanie rozwiązań równań ultradyskretnych jest bardzo trudne, ale zdarzają się wyjątki. Następujący przykład pochodzi z pracy [2]. W równaniu dyskretnym 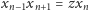 wprowadzamy nowe zmienne 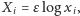 otrzymując ultradyskretne równanie 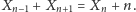 Szczęśliwie jest to po prostu równanie liniowe, więc Mathematica potrafi je rozwiązać: