Stowarzyszenie na rzecz Edukacji Matematycznej
O LXIV Olimpiadzie Matematycznej
W LXIV Olimpiadzie Matematycznej wzięło udział 1464 uczniów. Do zawodów drugiego stopnia zakwalifikowano 572 osoby, a do finału zorganizowanego przez I Liceum Ogólnokształcące im. Józefa Bema w Ostrołęce, obchodzące stulecie swego istnienia, zaproszono 121 młodych ludzi. Wszystkie zadania wraz z rozwiązaniami są dostępne na stronie internetowej Olimpiady: www.om.edu.pl. W pierwszym stopniu najtrudniejsze było zadanie ósme, ale i tak rozwiązało je poprawnie ponad 125 osób. Nie było więc zadania bardzo trudnego, bo takie są rozwiązywane jedynie przez kilka osób w kraju.
W zawodach okręgowych najtrudniejsze było zadanie szóste:
Zadanie (6).
Rozstrzygnąć, czy istnieją takie czworościany
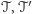 o ścianach
odpowiednio
o ścianach
odpowiednio
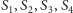 oraz
oraz
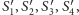 że dla
że dla
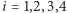 trójkąt
trójkąt
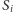 jest podobny do trójkąta
jest podobny do trójkąta
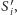 ale
mimo to czworościan
ale
mimo to czworościan
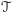 nie jest podobny do czworościanu
nie jest podobny do czworościanu
Rozwiązało je poprawnie czternastu zawodników. Nie przytaczamy
rozwiązania tego zadania, bo jest mu poświęcony artykuł Marcina Kuczmy na
stronie 18. Warto jednak nadmienić, że wielu uczestników opisywało
nieistniejące czworościany, podając np. długości ich krawędzi. Nie
troszczyli się o to, by suma kątów płaskich przy jednym wierzchołku była
mniejsza od
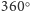 lub by suma dwóch kątów płaskich przy jednym
wierzchołku była większa od trzeciego kąta płaskiego przy nim. Jest to zapewne
częściowo związane z praktyczną rezygnacją z nauczania stereometrii
w szkołach.
lub by suma dwóch kątów płaskich przy jednym
wierzchołku była większa od trzeciego kąta płaskiego przy nim. Jest to zapewne
częściowo związane z praktyczną rezygnacją z nauczania stereometrii
w szkołach.
Nieco łatwiejsze było zadanie piąte, rozwiązane przez dziewiętnastu uczniów.
Zadanie (5). Rozstrzygnąć, czy wielomian o współczynnikach całkowitych, który jest funkcją różnowartościową na zbiorze liczb wymiernych, musi też przyjmować różne wartości dla różnych argumentów rzeczywistych.
Wspólną cechą obu tych zadań, decydującą o ich trudności, było to, że najpierw należało sformułować tezę, a dopiero potem ją uzasadnić. Niestety, oba pojawiły się w sobotę (byłem za), czyniąc drugi dzień zawodów bardzo trudnym.
W finale pojawiły się dwa bardzo trudne zadania: trzecie (dwie szóstki i 119 zer) i szóste (dwie szóstki, cztery piątki, dwie dwójki i 113 zer). Oba wymagały właściwego pomysłu, a wiedzy tylko z gimnazjum!
Zadanie (5).
Wykazać, że
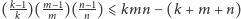 dla dowolnych
trzech różnych liczb całkowitych
dla dowolnych
trzech różnych liczb całkowitych
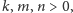 .
.
Zadanie to sprawdzano najdłużej. W niektórych pracach pojawiły się tak długie przekształcenia, że sprawdzaliśmy je za pomocą komputera. A po „wyczyszczeniu” straciły na „powadze”, co zaraz pokażemy. Niech

Symetria pozwala założyć, że
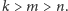 Jeśli
Jeśli
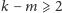 i
i
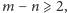 to
to
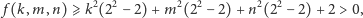 |
więc nierówność zachodzi w tej sytuacji. Niech
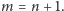 Wtedy:
Wtedy:

Ponieważ
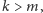 więc
więc
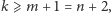 zatem:
zatem:
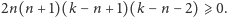 Analogicznie prawdziwy jest
wzór:
Analogicznie prawdziwy jest
wzór:

Nierówność jest prawdziwa dla każdej trójki liczb całkowitych
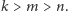 A dla niecałkowitych liczb czasem nie jest, np. gdy
A dla niecałkowitych liczb czasem nie jest, np. gdy
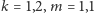 i
i
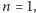 to prawa strona jest równa
to prawa strona jest równa
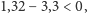 a lewa –
a lewa –