Może się nam to skojarzyć na przykład z cyframi rzymskimi w zakresie od jeden do trzech (I, II, III), chociaż dalej już oczywiście nie. Przy liczbach większych sposób kardynalny jest niezwykle niepraktyczny, o czym łatwo się przekonać, próbując tak zapisać na przykład 100. Fachowo rzecz ujmując, nieefektywność tego systemu wiąże się z subityzacją. Jest to umiejętność oszacowania liczby widocznych elementów bez liczenia ich. Dla przykładu, chyba od razu widać, że na rysunku 1 są trzy kolorowe kwadraty. Jednakże stwierdzenie, ile kwadratów znajduje się na rysunku 2, zajmuje więcej czasu - trzeba je policzyć. Według badań, opublikowanych w 1995 roku przez Brytyjskie Stowarzyszenie Psychologiczne, ta umiejętność natychmiastowego stwierdzenia liczby elementów działa do około 5 elementów. Właśnie przez to ograniczenie system kardynalny jest stosowany jedynie w językach, których użytkownicy nie mają potrzeby opisywania większych liczb. Jest ich naprawdę niewiele.

Rys. 1

Rys. 2

Pozostałe języki używają drugiego sposobu opisywania liczb - systemu ordynalnego. Działa on tak, że wybranym liczbom przyporządkowuje się różne symbole, które je opisują. Oczywiście, nie moglibyśmy przyporządkować różnych symboli wszystkim liczbom. Pozostałe opisuje się, używając kombinacji wcześniej ustalonych symboli. To właśnie jest system liczbowy. Często jest on oparty na jednej liczbie, czyli podstawie. We wspomnianym wcześniej systemie kardynalnym podstawą jest jedynka. W systemie dwójkowym, używanym w informatyce, podstawa to liczba 2. Z kolei my używamy systemu dziesiętnego. Ale skąd wzięły się te liczby? Dlaczego akurat 10, a nie 11? Spróbujmy na to odpowiedzieć. Źródło jedynki jest dość oczywiste. Dwójka wynika ze sposobu przekazywania informacji w komputerze: albo prąd płynie, albo nie. Skoro możemy używać tylko dwóch "znaków", to system musi być dwójkowy. W przypadku 10 najprawdopodobniej wyniknęło to z liczby palców u rąk człowieka. Do dziesięciu możemy policzyć na palcach, potem już nie. Bardzo podobne źródło mają systemy oparte na liczbie dwadzieścia, gdzie liczono zarówno palce rąk, jak i nóg. Właśnie liczba dwadzieścia pojawia się dość często, na przykład w kulturach Majów, Azteków i Celtów, czasem jedynie jako część, na przykład w języku mańskim (język Celtów, używany na wyspie Man).

Zapis liczb w języku mańskim jest podobny do zapisu liczb po polsku czy angielsku, z istotną różnicą związaną z dwudziestką. Liczby od 1 do 20 czyta się "normalnie": 8 to hocht, 18 to hocht-jeig. Powyżej 20 przechodzimy natomiast na system "bardziej" dwudziestkowy: 28 to hocht as feed, czyli dosłownie osiem i dwadzieścia, 38 to hocht-jeig as feed, czyli osiemnaście i dwadzieścia, a 98 to kiare feed as hocht-jeig, czyli cztery dwudziestki i osiemnaście. Jest to dla mnie niezmiernie ciekawy sposób liczenia, gdyż nie jest do końca ani systemem dziesiętnym ani dwudziestkowym.

Innym niezwykłym językiem pod względem zapisu liczb jest Telefol. Nie jest to nazwa sieci komórkowej, a język używany przez około 5400 osób w Papui Nowej Gwinei. Jest wyjątkowy z wielu względów, ale przede wszystkim przez sposób liczenia. Otóż liczą oni w systemie dwudziestosiódemkowym. Na pierwszy rzut oka liczba 27 może się wydawać wzięta znikąd, a sam system bardzo niepraktyczny. Ma on jednak pewne uzasadnienie. Ludzie mówiący w Telefol liczą nie tylko na palcach! Ich przodkowie byli bardziej kreatywni i wymyślili sposób liczenia na całej górnej połowie ciała. Zaczyna się od lewej dłoni, od małego palca do kciuka (liczby 1-5), następnie nadgarstek (6), przedramię (7), łokieć (8), nadramię (9), ramię (10), lewa strona szyi (11), ucho (12), oko (13) i nos (14). Następnie powtarza się to w odwrotnej kolejności po prawej stronie ciała (bez nosa, który już był policzony) - i tak mały palec prawej ręki ma przypisaną liczbę właśnie 27. To przełożyło się na język i utworzenie całego systemu liczbowego.

Jeszcze jeden interesujący system liczbowy, o którym warto wspomnieć, to system dwunastkowy. Jest on ciekawy dlatego, że istnieje względnie duża grupa ludzi, którzy nawołują do zmiany systemu z dziesiętnego na dwunastkowy, argumentując to dużo większą praktycznością. Występuje w nim 12 symboli: liczby 0-9 oznaczane są tak samo, jak w dziesiętnym, 10 staje się 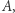a 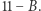Przez to "dziesiętna" liczba 23 zostanie w takim systemie zapisana jako 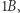a "dziesiętna" liczba 100 jako 84. Wydaje się to być jedynie dodatkową komplikacją, lecz ten system rzeczywiście ma wiele zalet. Przede wszystkim liczba 12 posiada aż sześć dzielników, a 10 posiada jedynie cztery. Przekłada się to na wiele ułatwień. Na przykład, kolejne wielokrotności liczby 3 zapisywane są następująco: 3, 6, 9, 10, 13, 16, 19, 20, 23, … Podobną "regularność" mają kolejne wielokrotności 4. Można zauważyć, że ostatnie cyfry tych liczb powtarzają się w krótkich ciągach cyfr, co w systemie dziesiętnym zachodzi tylko dla dwójki i piątki. Jednakże to nie mnożenie jest największą zaletą tego systemu, a dzielenie. Rozważmy najczęstsze podziały. Będą to dzielenia przez małe liczby, jak dwa, trzy czy cztery. Jeżeli chcemy 100 złotych podzielić na trzy, to w systemie dziesiętnym będzie to 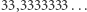Z kolei w systemie dwunastkowym wynik zapiszemy jako 29,4. Nie ma nieskończonego okresu, zamiast tego tylko jedna liczba po przecinku. Ta zaleta wielu dzielników liczby będącej podstawą nie jest niczym nowym. Została zauważona już w starożytności przez Babilończyków. Utworzyli oni swój system liczbowy na podstawie liczby 60, która ma aż dwanaście dzielników. To właśnie stamtąd wywodzi się także nasz sposób pomiaru czasu - 60 sekund w minucie, 60 minut w godzinie. Jednak ten system miał pewną wadę, mianowicie konieczność użycia (i zapamiętania) sześćdziesięciu różnych znaków.

Na koniec chciałbym przytoczyć ciekawostkę z okresu Rewolucji Francuskiej, podczas której sposób liczenia zmieniał się w bardzo dziwny sposób. Okres trwający od 1789 do 1799 roku przyniósł radykalne próby wprowadzenia wszędzie systemu dziesiętnego. Może się to wydawać dziwne, gdyż we Francji tego systemu używano wtedy już od setek lat, lecz rewolucjoniści chcieli pozbyć się wszystkich innych sposobów liczenia. I tak wprowadzono dziesięciodniowe tygodnie, doba została podzielona na 10 godzin, a godzina na 100 minut. Tak jak większość zmian w tamtym okresie, były one wprowadzone siłą, bez praktycznego uzasadnienia ani w sumie większego powodu niż "bo tak". Ten podział był tak niepraktyczny, że już po dwunastu (!) latach nikt go nie używał.