Mała Delta
Nieskończoność
Problemy starożytnych
Jednym z naturalnych skojarzeń z nieskończonością są duże, bardzo duże liczby. Tak bardzo, że trudno je sobie wyobrazić, a intuicja nie pomaga. Możemy jednak o nich pomyśleć. Czytając doniesienia o wydatkach z budżetu państwa lub tym bardziej o światowej gospodarce, łatwo pogubić się w milionach, miliardach i bilionach. I chociaż wiemy, że w bilionie 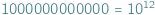 mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.
mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.
Choć i tu granica może być płynna, czego dowodzi przedstawiony poniżej banknot opiewający na kwotę stu bilionów dolarów Zimbabwe. Warto tu zwrócić uwagę na nieintuicyjne przesunięcie nazewnictwa liczb między polskim i angielskim językiem - polski miliard to angielski billion, a więc angielski trillion to po polsku bilion. Banknot jest wynikiem hiperinflacji w Zimbabwe, która w rekordowym listopadzie 2009 roku wyniosła aż około 80 miliardów procent w skali miesięcznej.

Każdy czytelnik zdaje sobie jednak sprawę, że można myśleć bez trudu o większych liczbach. O ile sto bilionów to 14 zer za jedynką, o tyle liczbę mającą za jedynką 100 zer, czyli 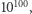 zwykło się nazywać googol. Zbieżność nazwy ze znaną firmą nie jest przypadkowa, jej założyciele właśnie tą liczbą się inspirowali, a różnica w nazwie, podobno, jest wynikiem literówki. No dobrze, widać, że googol to duża liczba. Ale jak duża? Co jest większe: googol czy liczba komórek w ciele człowieka? Googol czy liczba atomów w ciele człowieka? Googol czy liczba atomów na kuli ziemskiej? Liczba atomów w Układzie Słonecznym? W naszej galaktyce? W obserwowalnym Wszechświecie? Okazuje się, że na wszystkie te pytania prawidłową odpowiedzią jest: googol jest większy (rzędy wielkości tych liczb szacowane są kolejno na
zwykło się nazywać googol. Zbieżność nazwy ze znaną firmą nie jest przypadkowa, jej założyciele właśnie tą liczbą się inspirowali, a różnica w nazwie, podobno, jest wynikiem literówki. No dobrze, widać, że googol to duża liczba. Ale jak duża? Co jest większe: googol czy liczba komórek w ciele człowieka? Googol czy liczba atomów w ciele człowieka? Googol czy liczba atomów na kuli ziemskiej? Liczba atomów w Układzie Słonecznym? W naszej galaktyce? W obserwowalnym Wszechświecie? Okazuje się, że na wszystkie te pytania prawidłową odpowiedzią jest: googol jest większy (rzędy wielkości tych liczb szacowane są kolejno na 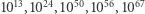 i
i 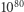 ).
).
Ale przecież możemy myśleć o liczbach jeszcze większych. Na przykład o liczbie w postaci jeden i googol zer, czyli liczbie 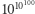 zwanej googolplex. Nie bez przyczyny nie drukujemy jej tu w pełnej dziesiętnej wersji - skoro atomów w obserwowalnym Wszechświecie jest mniej niż googol, nie starczyłoby ich, gdyby na każdym atomie chcieć umieścić jedną cyfrę googolplexa… Fakt, że w ogóle o takiej liczbie tu dyskutujemy, można uznać za komplement dla ludzkiego umysłu. A przecież nadal rozważamy tylko pewien skończony początek zbioru liczb naturalnych, nieskończoności tego zbioru dotykając tylko ulotnie poprzez świadomość, że dla każdej liczby naturalnej możemy znaleźć liczbę od niej większą.
zwanej googolplex. Nie bez przyczyny nie drukujemy jej tu w pełnej dziesiętnej wersji - skoro atomów w obserwowalnym Wszechświecie jest mniej niż googol, nie starczyłoby ich, gdyby na każdym atomie chcieć umieścić jedną cyfrę googolplexa… Fakt, że w ogóle o takiej liczbie tu dyskutujemy, można uznać za komplement dla ludzkiego umysłu. A przecież nadal rozważamy tylko pewien skończony początek zbioru liczb naturalnych, nieskończoności tego zbioru dotykając tylko ulotnie poprzez świadomość, że dla każdej liczby naturalnej możemy znaleźć liczbę od niej większą.
Już starożytni greccy matematycy stykali się z tego typu nieskończonością, zwaną czasem nieskończonością potencjalną. Prostą można przedłużyć dowolnie daleko, odcinek można podzielić na dowolnie wiele części - tak mówiono już w ówczesnej matematyce, i tego nie dało się uniknąć. Nikt natomiast ze starożytnych matematyków nie powiedziałby, że prostą można przedłużać w nieskończoność lub że liczb jest nieskończenie wiele. Nie rozważano podziału odcinka na nieskończenie wiele części. Unikano takiej aktualnej nieskończoności jak ognia - była postrzegana jako źródło niechcianej wówczas w matematyce nieścisłości i paradoksów. Nie rozważano więc istnienia nieskończonych zbiorów.
Chociażby słynny dowód z "Elementów" Euklidesa, o którym powiedzielibyśmy obecnie, że dowodzi istnienia nieskończenie wielu liczb pierwszych, tak naprawdę mówił o tym, że można znaleźć dowolnie wiele takich liczb. Istotnie, jeśli mamy już 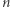 liczb pierwszych
liczb pierwszych 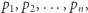 to rozważmy liczbę
to rozważmy liczbę 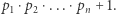 Ona nie dzieli się przez żadną z dotychczas znalezionych liczb, więc albo ona sama jest pierwsza, albo dzieli się przez inną, nierozważaną jeszcze liczbę pierwszą
Ona nie dzieli się przez żadną z dotychczas znalezionych liczb, więc albo ona sama jest pierwsza, albo dzieli się przez inną, nierozważaną jeszcze liczbę pierwszą 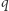 - czyli tak czy inaczej mamy jeszcze jedną liczbę pierwszą.
- czyli tak czy inaczej mamy jeszcze jedną liczbę pierwszą.
Problemem były też wielkości, które dziś nazywamy niewymiernymi. Natknęli się na nie Pitagorejczycy, zauważając, że stosunek przekątnej i boku kwadratu nie da się wyrazić stosunkiem liczb naturalnych. Był to nie lada problem, bo ta obserwacja podważała filozoficzne przekonanie, że wszystko jest liczbą, wszystko liczbami (w domyśle naturalnymi) da się opisać. Co więcej, Pitagorejczycy upatrywali w stosunkach niskich liczb naturalnych, sprawdzonych na przykładzie muzyki, harmonii w świecie. Brak harmonii w tak doskonałej figurze jak kwadrat był więc co najmniej zaskakujący. Problem jest jednak bardzo bliski problemowi z nieskończonością, bo po pewnym czasie zorientowano się, że stosunek przekątnej i boku kwadratu można przybliżać stosunkami liczb naturalnych. Notując we współczesny sposób spostrzeżenia Teajtetosa (matematyka z IV wieku p.n.e), napisalibyśmy, że
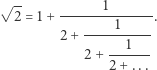
Tak więc stosunki w kwadracie da się opisać harmonią małych liczb naturalnych, z tym że nieskończenie wielu. Jeszcze lepiej wygląda analogiczne przedstawienie złotej proporcji - zobaczymy w nim same jedynki. Warto jednak zwrócić uwagę, że do pełnej akceptacji tego typu geometrycznych stosunków jako liczb niezbędne jest lepsze zrozumienie pojęć związanych z nieskończonością, którego ówcześni matematycy nie mieli.

Stąd też słynne paradoksy Zenona z Elei, w których sprzeczność powstaje w wyniku rozważań skończonych części nieskończonych ciągów. Najsłynniejszy jest chyba ten o żółwiu i Achillesie, w którym Achilles ściga żółwia, biegnąc z dwa razy większą prędkością od niego, ale startując 40 metrów za nim. Paradoks orzeka, że Achilles nigdy nie dogoni żółwia, bo zanim przebiegnie do miejsca, gdzie startował żółw, żółw będzie już 20 metrów dalej. Gdy jednak Achilles przebiegnie te dodatkowe 20 metrów, żółw będzie jeszcze o 10 metrów dalej. I tak dalej - rozumowanie możemy prowadzić dowolnie długo. Nie wiemy do końca, jaka była intencja (Zenon z pewnością wiedział, że Achilles dogoni żółwia), która stała za tymi paradoksami, bo znamy je tylko z przekazu Arystotelesa, który cytował je po to, żeby je rozwikłać (na miarę możliwości jego epoki). Na pewno paradoksy te wskazują słabości w rozumieniu i opisywaniu nieskończonych procesów w starożytnej matematyce. Dzisiaj powiedzielibyśmy po prostu, że paradoks sprowadza się do obliczenia sumy szeregu 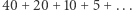 i że wychodzi 80 - i po przebiegnięciu tylu metrów Achilles rzeczywiście żółwia dogoni.
i że wychodzi 80 - i po przebiegnięciu tylu metrów Achilles rzeczywiście żółwia dogoni.
Żeby jednak pojęcia sumy nieskończonego szeregu i granicy nieskończonego ciągu zostały porządnie zrozumiane i zdefiniowane przez matematyków, potrzeba było dwóch dodatkowych tysiącleci. Obecnie pojęcia te należą do kanonu matematyki. Skąd zatem wiemy, że nieskończone zbiory istnieją? Odpowiedź może nie zadowolić części Czytelników. Istnienie nieskończonego zbioru zostało przyjęte po prostu jako jeden z aksjomatów we współczesnej teorii zbiorów. Czy to wystarczające rozwiązanie dla dylematu starożytnych greckich matematyków?