Rozważmy równanie różniczkowe

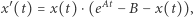wywodzące się z pewnego modelu matematycznego przebiegu choroby zakaźnej. Nie wnikając w szczegóły modelu i w konkretne wartości parametrów 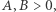uznajmy, że szukana funkcja 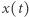odpowiada (przeskalowanej) liczbie osób zarażonych przypadającej na jednostkę powierzchni w chwili czasu 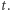Zakładamy, że w chwili 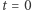liczba chorych jest niewielka, ale dodatnia.

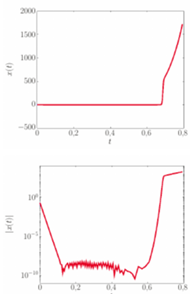
Traktując to równanie standardowym pakietem komputerowym MATLAB, dostajemy rozwiązanie o "rozsądnym" przebiegu, o czym możemy przekonać się, patrząc na rysunek na dole: na początku, przez dłuższy czas populacja chorych utrzymuje się na poziomie bliskim (kto wie, może nawet równym?) zeru, a następnie zaczyna szybko rosnąć.

Jednak gdy dokładnie to samo rozwiązanie zobrazujemy inaczej: na wykresie, którego pionowa oś jest w skali logarytmicznej (rysunek na dole) - ujawnią się dodatkowe informacje. Okazuje się (czego wcześniej nie widzieliśmy), że na początku rozwiązanie maleje, ale potem na dłużej stabilizuje się na poziomie 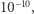by na koniec (co wszak widzieliśmy na poprzednim obrazku) szybko urosnąć. Ze względu na skalę logarytmiczną możemy mieć złudzenie, że ostatnia faza wzrostu jest dosyć wolna - lecz to właśnie jest tylko złudzenie.

No dobrze, dzięki użyciu innej skali zyskaliśmy wgląd w zachowanie się rozwiązania dla bardzo małych wartości (skala liniowa to uniemożliwiała) - ale czy cokolwiek więcej z tego wynika? Owszem! Niepokój może budzić to, że w zakresie bardzo małych wartości funkcja 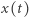zachowuje się nieregularnie: teoria równań różniczkowych przewiduje zaś, że nasze rozwiązanie powinno mieć gładki przebieg, niezależnie od tego, czy skala osi jest logarytmiczna, czy liniowa. Jednak z drugiej strony, wahania są przecież bardzo drobne, oscylujące wokół wartości 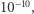czyli prawie zera - więc może nie ma czym się przejmować?

Może lepiej nie szukać dziury w całym, tzn. nie przyglądać się aż tak dokładnie - w końcu przecież sensownie i estetycznie wyglądającemu - wykresowi na górze? Odpowiemy w następnym numerze Delty.