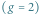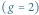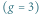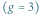Nagrody Nobla
Maryam Mirzakhani (1977-2017)

Photo: Stanford University.
Maryam Mirzakhani (1977-2017)
W matematyce nie przyznaje się Nagrody Nobla, jednakże od ustanowienia w 1936 roku Medalu Fieldsa (od nazwiska kanadyjskiego matematyka Johna Charlesa Fieldsa) wyróżnienie to stało się najważniejszą nagrodą w tym obszarze badań. Fields uczestniczył w jej powstaniu, zaprojektował towarzyszący jej medal i pozostawił funduszowi Medalu Fieldsa kwotę 47000 dolarów kanadyjskich. Finansowy dodatek do Medalu to 15000 dolarów kanadyjskich, znacznie mniej niż 8 milionów szwedzkich koron (około 800000 euro) przyznawanych w ramach Nagrody Nobla, mimo to w oczach matematyków prestiż tego wyróżnienia jest nie mniejszy. Obecnie w matematyce przyznawana jest także Nagroda Abela oraz inne wysoko cenione wyróżnienia, jednak najdłuższa tradycja stoi za Medalem Fieldsa.
W 1936 roku medalistami Fieldsa zostali Lars Ahlfors i Jesse Douglas. Po dłuższej przerwie, w 1950 roku medale zdobyli Laurent Schwarz oraz Atle Selberg. Od tamtej pory są one przyznawane co cztery lata 2-4 matematykom i wręczane na Międzynarodowych Kongresach Matematyków. Pierwszą kobietę nagrodzono Medalem Fieldsa dopiero w 2014 roku. Była nią Maryam Mirzakhani, urodzona w Iranie, pracująca na Uniwersytecie Stanforda w Stanach Zjednoczonych. Jej wielce obiecującą karierę przerwała w 2017 roku śmierć spowodowana rakiem piersi. Miała zaledwie 40 lat. To, co było tragedią dla matematyki, znacznie mocniej dotknęło jej rodzinę: męża i 6-letnią wówczas córkę Anahitę.

Maryam Mirzakhani urodziła się w Teheranie 3 maja 1977 roku jako córka Ahmada, inżyniera elektryka. Jej wybitne zdolności ujawniły się bardzo wcześnie. Edukację rozpoczęła w teherańskiej szkole Farzanegan, prowadzonej przez Narodową Organizację Rozwoju Wybitnych Talentów (której nazwa sama się tłumaczy). W 1994 roku znalazła się wśród uczestników Międzynarodowej Olimpiady Matematycznej, elitarnych corocznych zawodów matematycznych dla licealistów, i jako pierwsza kobieta z Iranu zdobyła złoty medal. W kolejnym roku uzyskała na Międzynarodowej Olimpiadzie komplet punktów i ponownie złoty medal, czego wcześniej nie dokonał nikt z Iranu.
W 1999 roku Mirzakhani ukończyła studia matematyczne na Uniwersytecie Technologicznym Sharif, nazywanym często "irańskim MIT", czołowej irańskiej uczelni w zakresie nauk inżynieryjnych i fizycznych. Podjęła studia doktoranckie w Stanach Zjednoczonych pod opieką naukową Curtisa McMullena, medalisty Fieldsa. McMullen zajmował się dynamiką zespoloną, geometrią hiperboliczną i tematami pochodnymi, w tych obszarach rozpoczęła też badania Maryam Mirzakhani. W 2004 roku dołączyła do zespołu badawczego w Clay Mathematics Institute (w Cambridge w stanie Massachusetts) i uzyskała stanowisko profesorskie w Princeton. Wyszła za mąż za Jana Vondráka, czeskiego informatyka zajmującego się także zastosowaniami matematyki, zatrudnionego na Uniwersytecie Stanforda. Mirzakhani przeniosła się na tę uczelnię w 2008 roku.
Dziedzina, którą uprawiała, teoria przestrzeni moduli powierzchni Riemanna, jest bardzo techniczna, zatem opisanie jej zajmie nam trochę miejsca. Zacznijmy od liczb zespolonych i analizy zespolonej. Kwadrat dowolnej liczby rzeczywistej jest nieujemny, zatem nie istnieją rzeczywiste pierwiastki kwadratowe z liczb ujemnych. Jednakże w połowie XVI wieku włoscy algebraicy zaczęli dostrzegać matematyczny sens pierwiastków kwadratowych z liczb ujemnych, choć ich znaczenie fizyczne pozostawało niejasne. Kluczowym momentem stało się wprowadzenie nowego rodzaju liczby, liczby "urojonej", oznaczanej dziś jako 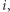 której kwadrat jest równy
której kwadrat jest równy  Prowadzi to do liczb zespolonych postaci
Prowadzi to do liczb zespolonych postaci  na których działania wykonuje się zgodnie ze znanymi regułami algebraicznymi, uwzględniając, że
na których działania wykonuje się zgodnie ze znanymi regułami algebraicznymi, uwzględniając, że 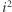 trzeba zastąpić przez
trzeba zastąpić przez 

Ostatecznie ta nowa koncepcja uzyskała ścisłe podstawy w XIX wieku, dzięki Carlowi Friedrichowi Gaussowi i Williamowi Rowanowi Hamiltonowi: liczba zespolona to para liczb rzeczywistych 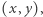 a działania na takich parach określają konkretne reguły. Motywację dla takiej definicji stworzyli poprzednicy, interpretując liczby zespolone jako punkty płaszczyzny, tak jak to robili Caspar Wessel w 1797 roku i Jean-Robert Argand w 1808. Jednak już dużo wcześniej matematycy starali się ambitnie zajść dalej. W 1702 roku Jan Bernoulli próbował obliczyć całkę z odwrotności funkcji kwadratowej
a działania na takich parach określają konkretne reguły. Motywację dla takiej definicji stworzyli poprzednicy, interpretując liczby zespolone jako punkty płaszczyzny, tak jak to robili Caspar Wessel w 1797 roku i Jean-Robert Argand w 1808. Jednak już dużo wcześniej matematycy starali się ambitnie zajść dalej. W 1702 roku Jan Bernoulli próbował obliczyć całkę z odwrotności funkcji kwadratowej 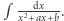
Gdy funkcja kwadratowa rozkłada się na dwa czynniki liniowe rzeczywiste, można jej odwrotność rozłożyć na sumę ułamków prostych, co prowadzi do wyrażeń logarytmicznych. Gorzej, gdy takiego rozkładu na czynniki rzeczywiste nie ma, jak w przypadku funkcji  Istnieją jednak czynniki zespolone
Istnieją jednak czynniki zespolone  i w takim przypadku Bernoulli stosował logarytmy zespolone, nie wyjaśniając, co oznaczają. W 1712 roku wdał się w tej kwestii w zażarty spór z Gottfriedem Wilhelmem Leibnizem, który uważał, że logarytm liczby ujemnej powinien być liczbą zespoloną, podczas gdy Bernoulli nalegał, iż jest to liczba rzeczywista. W 1749 roku Leonhard Euler przyznał rację Leibnizowi. Bernoulli, broniąc przeciwnego poglądu, zapomniał o tym, że całka nieoznaczona jest dana z dokładnością do stałej, która w tym przypadku jest liczbą zespoloną. Tak więc, na przykład,
i w takim przypadku Bernoulli stosował logarytmy zespolone, nie wyjaśniając, co oznaczają. W 1712 roku wdał się w tej kwestii w zażarty spór z Gottfriedem Wilhelmem Leibnizem, który uważał, że logarytm liczby ujemnej powinien być liczbą zespoloną, podczas gdy Bernoulli nalegał, iż jest to liczba rzeczywista. W 1749 roku Leonhard Euler przyznał rację Leibnizowi. Bernoulli, broniąc przeciwnego poglądu, zapomniał o tym, że całka nieoznaczona jest dana z dokładnością do stałej, która w tym przypadku jest liczbą zespoloną. Tak więc, na przykład, 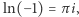 a nie 0, jak sądził Bernoulli.
a nie 0, jak sądził Bernoulli.
Atakowanie analizy funkcji zespolonych przed dobrym opanowaniem algebry liczb zespolonych wyglądało na próbę biegania przed nauką chodzenia. Analiza była jednak o wiele ciekawsza, zapowiadała potencjalne korzyści w fizyce matematycznej, gdzie można byłoby ją stosować do rozwiązywania równań różniczkowych cząstkowych, takich jak równanie Laplace'a, ważne w badaniach grawitacji, magnetyzmu czy elektryczności.
Euler zdawał sobie sprawę z tego, że choć 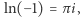 to jest to tylko jedna z nieskończenie wielu możliwych wartości. Istotnie, z równości
to jest to tylko jedna z nieskończenie wielu możliwych wartości. Istotnie, z równości 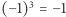 wynika, że
wynika, że  musi być także równy
musi być także równy 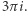 Czy zatem
Czy zatem 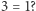 Gdyby tak było, liczby zespolone okazałyby się absurdalne. Euler wszakże tak nie uważał. Przecież pierwiastkami kwadratowymi z 1 są zarówno
Gdyby tak było, liczby zespolone okazałyby się absurdalne. Euler wszakże tak nie uważał. Przecież pierwiastkami kwadratowymi z 1 są zarówno 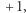 jak i
jak i  co wcale nie skłania nas do utożsamienia tych liczb i deklarowania, że pierwiastki kwadratowe to nonsens. Pierwiastek kwadratowy jest po prostu wielowartościowy i podobnie, jak twierdził Euler, jest z logarytmem zespolonym, z tym, że o ile pierwiastek kwadratowy ma co najwyżej dwie wartości, o tyle logarytm ma ich nieskończenie wiele. W szczególności logarytmem liczby
co wcale nie skłania nas do utożsamienia tych liczb i deklarowania, że pierwiastki kwadratowe to nonsens. Pierwiastek kwadratowy jest po prostu wielowartościowy i podobnie, jak twierdził Euler, jest z logarytmem zespolonym, z tym, że o ile pierwiastek kwadratowy ma co najwyżej dwie wartości, o tyle logarytm ma ich nieskończenie wiele. W szczególności logarytmem liczby  jest każda liczba postaci
jest każda liczba postaci  dla nieparzystej liczby całkowitej
dla nieparzystej liczby całkowitej 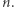 Z kolei, podnosząc do kwadratu, widzimy, że
Z kolei, podnosząc do kwadratu, widzimy, że  (o którym wiemy, że jest równy 0) to każda liczba postaci
(o którym wiemy, że jest równy 0) to każda liczba postaci 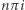 dla parzystej liczby całkowitej
dla parzystej liczby całkowitej 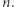 Znana nam wartość pojawia się dla
Znana nam wartość pojawia się dla 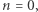 ale równie dobrze moglibyśmy przyjąć 2, 4, 6, albo nawet
ale równie dobrze moglibyśmy przyjąć 2, 4, 6, albo nawet 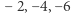 i tak dalej.
i tak dalej.
I teraz sprawa się komplikuje, jako że cokolwiek robimy w analizie zespolonej, na przykład, całkujemy funkcję wzdłuż krzywej na płaszczyźnie zespolonej, musimy zdecydować, którą wartość funkcji chcemy rozpatrywać. Gdy przesuwamy się po krzywej, ma sens zmienianie tej wartości w sposób ciągły, co prowadzi do ciekawej sytuacji. Jeśli, powiedzmy, zaczniemy od 1 i będziemy się przesuwać po okręgu jednostkowym w kierunku przeciwnym do ruchu wskazówek zegara, rozpatrywana liczba 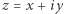 powraca do wartości 1. Jednocześnie jej logarytm
powraca do wartości 1. Jednocześnie jej logarytm 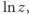 zmieniając się w sposób ciągły, musi rosnąć od 0 do
zmieniając się w sposób ciągły, musi rosnąć od 0 do 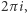 a po powrocie do punktu wyjścia wartość funkcji może różnić się od wartości początkowej.
a po powrocie do punktu wyjścia wartość funkcji może różnić się od wartości początkowej.
Decydujący krok wykonał tu Bernhard Riemann, wybitny myśliciel, geometra i autor pojęcia, które dziś nazywamy powierzchnią Riemanna. W przypadku logarytmu to coś w rodzaju spiralnych schodów, zakręcających się wokół środka płaszczyzny zespolonej i wspinających się o jeden poziom z każdym pełnym obrotem. Gdy  przesuwa się na poziomie parteru wzdłuż okręgu na płaszczyźnie zespolonej,
przesuwa się na poziomie parteru wzdłuż okręgu na płaszczyźnie zespolonej, 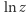 pokonuje zakręt na spiralnych schodach i trafia piętro wyżej. Tak więc to geometria powierzchni decyduje o tym, którą z wielu wartości należy rozpatrywać. Podobnie jest z pierwiastkiem kwadratowym, z tym, że tu mamy tylko dwa zakręty, a drugie piętro jest "tym samym" co parter: po dwóch obrotach wartość pierwiastka kwadratowego wraca do wartości początkowej.
pokonuje zakręt na spiralnych schodach i trafia piętro wyżej. Tak więc to geometria powierzchni decyduje o tym, którą z wielu wartości należy rozpatrywać. Podobnie jest z pierwiastkiem kwadratowym, z tym, że tu mamy tylko dwa zakręty, a drugie piętro jest "tym samym" co parter: po dwóch obrotach wartość pierwiastka kwadratowego wraca do wartości początkowej.

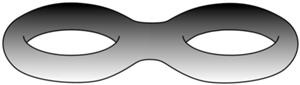
Po utożsamieniu przeciwległych boków kwadratu otrzymujemy torus.
Podstawowe pojęcia analizy zespolonej, takie jak różniczkowanie lub całkowanie wzdłuż krzywych, można uogólnić na powierzchnie Riemanna, stanowiące naturalny kontekst dla analizy zespolonej, gdyż rozwiązują problemy wynikające z wielowartościowości funkcji. To ich najistotniejsza właściwość. Niektóre powierzchnie Riemanna są "zwarte": nie mają brzegu, jednak zajmują skończony obszar, czego przykładem może być sfera Riemanna, czyli płaszczyzna zespolona "uzwarcona" przez dodanie punktu "w nieskończoności". Inny przykład wiąże się z funkcjami eliptycznymi, a więc takimi funkcjami zespolonymi 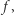 że
że 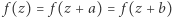 dla wszystkich
dla wszystkich 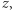 gdzie
gdzie 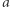 i
i  są dwiema niezależnymi liczbami zespolonymi. Wówczas wartości funkcji powtarzają się w dwóch kierunkach na płaszczyźnie zespolonej, co dzieli tę płaszczyznę na nieskończenie wiele jednakowych "kafli" w kształcie równoległoboku, z których jeden ma wierzchołki w punktach
są dwiema niezależnymi liczbami zespolonymi. Wówczas wartości funkcji powtarzają się w dwóch kierunkach na płaszczyźnie zespolonej, co dzieli tę płaszczyznę na nieskończenie wiele jednakowych "kafli" w kształcie równoległoboku, z których jeden ma wierzchołki w punktach 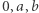 oraz
oraz 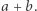 Na każdym kaflu funkcja przyjmuje te same wartości, wystarczy zatem wiedzieć, jak zachowuje się na jednym. Podwójna okresowość oznacza, że funkcja przyjmuje te same wartości na przeciwległych bokach kafla, a więc - po utożsamieniu przeciwległych boków - można wszystko sprowadzić do jednego kafla. Z topologicznego punktu widzenia wynikiem takiej konstrukcji jest torus, co pokazuje rysunek dla przypadku, gdy kafle są kwadratami.
Na każdym kaflu funkcja przyjmuje te same wartości, wystarczy zatem wiedzieć, jak zachowuje się na jednym. Podwójna okresowość oznacza, że funkcja przyjmuje te same wartości na przeciwległych bokach kafla, a więc - po utożsamieniu przeciwległych boków - można wszystko sprowadzić do jednego kafla. Z topologicznego punktu widzenia wynikiem takiej konstrukcji jest torus, co pokazuje rysunek dla przypadku, gdy kafle są kwadratami.
Zwartymi powierzchniami Riemanna są: sfery, torusy, torusy z dziurami. Liczbę 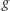 dziur nazywa się genusem. I tak, 0 jest genusem sfery, 1 genusem zwykłego torusa i co najmniej 2 jest genusem torusa z
dziur nazywa się genusem. I tak, 0 jest genusem sfery, 1 genusem zwykłego torusa i co najmniej 2 jest genusem torusa z  dziurami, gdy
dziurami, gdy 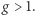
Struktura powierzchni Riemanna nie ogranicza się do topologii. W szczególności można w niej operować pojęciem odległości lub metryki. Geometria takiej metryki może być:
- euklidesowa - powierzchnią jest, na przykład, płaszczyzna zespolona lub tzw. "płaski" torus,
- eliptyczna - jedna z dwóch nieeuklidesowych geometrii, odpowiadająca powierzchni o dodatniej krzywiźnie, jak sfera Riemanna,
- hiperboliczna - druga z nieeuklidesowych geometrii, odpowiadająca powierzchni o ujemnej krzywiźnie, jak torus z
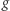 dziurami dla
dziurami dla 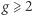 lub torus bez jednego punktu.
lub torus bez jednego punktu.
Jak widać, powierzchnie Riemanna stanowią bardzo obszerną dziedzinę matematyki, łączącą wiele rozmaitych pojęć.
Aby dokonać klasyfikacji wszystkich możliwych powierzchni Riemanna (ustalonego typu), matematycy wymyślili przestrzeń moduli, której każdy punkt reprezentuje określoną powierzchnię Riemanna. Taka przestrzeń ma swoją topologię, można zatem zdefiniować w niej pojęcie bliskości dwóch powierzchni, pozwalające opisać, co dzieje się z daną strukturą, gdy przekształca się ją w sposób ciągły w bliskie jej struktury tego samego typu.
Przyjrzyjmy się prostej analogii. Przypuśćmy, że zajmujemy się okręgami na płaszczyźnie. Każdy okrąg jest jednoznacznie wyznaczony przez trzy liczby: dwie współrzędne środka 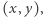 które są dowolnymi liczbami rzeczywistymi, oraz nieujemny promień
które są dowolnymi liczbami rzeczywistymi, oraz nieujemny promień 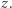 Przestrzeń moduli okręgów składa się więc ze wszystkich takich trójek
Przestrzeń moduli okręgów składa się więc ze wszystkich takich trójek 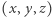 liczb rzeczywistych, że
liczb rzeczywistych, że 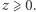 Topologicznie rzecz biorąc, jest to iloczyn kartezjański płaszczyzny
Topologicznie rzecz biorąc, jest to iloczyn kartezjański płaszczyzny  i nieujemnej półprostej rzeczywistej
i nieujemnej półprostej rzeczywistej 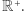 Dwa okręgi uznamy za bliskie w przestrzeni moduli, jeśli ich środki są blisko na płaszczyźnie oraz bliskie są długości ich promieni. To rozsądne wymaganie.
Dwa okręgi uznamy za bliskie w przestrzeni moduli, jeśli ich środki są blisko na płaszczyźnie oraz bliskie są długości ich promieni. To rozsądne wymaganie.
Doszliśmy wreszcie do historycznego punktu wyjścia dla badań Mirzakhami, możemy więc spróbować zrozumieć, co rzeczywiście zrobiła. W 2002 roku znalazła nowy dowód Hipotezy Wittena, dotyczącej przestrzeni moduli wszystkich krzywych algebraicznych. Edward Witten postulował istnienie związków między tą przestrzenią a niektórymi kwantowymi teoriami pola oraz całkowalnymi układami dynamiki hamiltonowskiej. Brak miejsca nie pozwala na głębsze wyjaśnienia, ale, w uproszczeniu, układ dynamiczny jest całkowalny, gdy zachowuje się w sposób regularny, niechaotyczny. Hipotezę Wittena pierwszy udowodnił Maxim Kontsevich w 1992 roku i dowód ten stał się jednym z wyników, które przyniosły mu Medal Fieldsa.
Ta krzywa na torusie przewija się pięć razy przez dziurę i zawija się dwa razy wokół korpusu.
Mirzakhani przedstawiła odmienny dowód, oparty na wzorze odkrytym przez Grega McShane'a. Rozważmy torus z usuniętym jednym punktem i nadajmy mu hiperboliczną strukturę geometryczną, traktując usunięty punkt jako punkt "w nieskończoności". Taka powierzchnia zawiera wiele zamkniętych geodezyjnych, czyli ścieżek o najmniejszej długości, zamykających się jak okrąg (wyobraźmy sobie owinięcie powierzchni elastyczną taśmą). Wszystkie takie ścieżki można podzielić na klasy homotopii tak, że dwie ścieżki należą do tej samej klasy, jeśli jedną z nich można przekształcić w drugą w sposób ciągły (wyobraźmy sobie popchnięcie elastycznej taśmy w nowe położenie). W przypadku torusa klasę homotopii wyznaczają dwie liczby całkowite: ile razy ścieżka przewija się przez dziurę torusa oraz ile razy zawija się wokół "korpusu" torusa.
Równość McShane'a stwierdza, iż
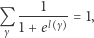
gdzie 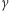 przebiega listę zamkniętych geodezyjnych, zawierającą po jednej z każdej klasy homotopii, a
przebiega listę zamkniętych geodezyjnych, zawierającą po jednej z każdej klasy homotopii, a 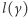 oznacza długość geodezyjnej
oznacza długość geodezyjnej  Mirzakhani użyła tej równości do ustalenia wzoru na objętość
Mirzakhani użyła tej równości do ustalenia wzoru na objętość 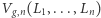 przestrzeni moduli wszystkich powierzchni genusu
przestrzeni moduli wszystkich powierzchni genusu 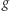 z
z 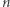 geodezyjnymi krzywymi brzegowymi o danych długościach
geodezyjnymi krzywymi brzegowymi o danych długościach  Objętość okazuje się być wielomianem względem kwadratów tych długości, którego współczynnikami są wymierne wielokrotności potęg liczby
Objętość okazuje się być wielomianem względem kwadratów tych długości, którego współczynnikami są wymierne wielokrotności potęg liczby 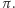 Wielomiany te kodują informację topologiczną o przestrzeni moduli i spełniają te same relacje co niektóre wielomiany występujące w Hipotezie Wittena. Umożliwiło to zupełnie odmienny nowy dowód Hipotezy.
Wielomiany te kodują informację topologiczną o przestrzeni moduli i spełniają te same relacje co niektóre wielomiany występujące w Hipotezie Wittena. Umożliwiło to zupełnie odmienny nowy dowód Hipotezy.
Nowe metody Mirzakhani doprowadziły ją do wzorów określających częstość występowania geodezyjnych różnych topologicznych typów. Na przykład, dokładnie 1/7 wszystkich zamkniętych pętli na torusie genusu 2 ma tę własność, że rozcięcie wzdłuż pętli rozspójnia torus.
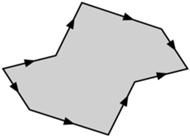
Powierzchnia translacyjna.
Później Mirzakhani zajęła się dynamiką w przestrzeniach moduli, w których punkty (reprezentujące krzywe lub inne obiekty topologiczne) poruszają się zgodnie z określonymi regułami (wyobraźmy sobie znowu elastyczną taśmę wędrującą po powierzchni pod wpływem danych sił). Badała, na przykład, przestrzenie moduli powierzchni translacyjnych, stanowiących uogólnienie konstrukcji torusa przez sklejenie przeciwległych boków kwadratu - zamiast kwadratu bierze się dowolny wielokąt na płaszczyźnie, który ma parami równoległe boki równej długości, skleja się boki z tej samej pary. Dochodzi jeszcze dodatkowy warunek: po sklejeniu łączny kąt wokół każdego wierzchołka musi być całkowitą wielokrotnością 
Liniowe przekształcenie płaszczyzny o wyznaczniku 1 zachowuje równoległość i równą długość w parach boków, zatem takie przekształcenia działają jak grupa symetrii przestrzeni moduli. Tę grupę oznacza się symbolem 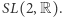 Można teraz pytać o powierzchnie translacyjne, które da się otrzymać z powierzchni danej za pomocą takich przekształceń; dokładniej, jakie powierzchnie można dowolnie blisko przybliżać taką przekształconą powierzchnią (leżą w domknięciu orbity tej powierzchni w
Można teraz pytać o powierzchnie translacyjne, które da się otrzymać z powierzchni danej za pomocą takich przekształceń; dokładniej, jakie powierzchnie można dowolnie blisko przybliżać taką przekształconą powierzchnią (leżą w domknięciu orbity tej powierzchni w 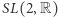 )? Zasadne wydaje się przypuszczenie, że tworzą one jakiś rodzaj skomplikowanego fraktala, ale jest to przypuszczenie błędne, jak wykazała Mirzakhani w pracy wspólnej z Alexem Eskinem i Amirem Mohammadim. Odpowiedź poprawna: takie powierzchnie tworzą rozmaitość, czyli wielowymiarowy odpowiednik powierzchni, określoną układem równań liniowych. Bardziej technicznie, autorzy udowodnili The Magic Wand Conjecture (hipotezę czarodziejskiej różdżki, teraz już twierdzenie): domknięcie orbity dowolnej płaskiej powierzchni translacyjnej w
)? Zasadne wydaje się przypuszczenie, że tworzą one jakiś rodzaj skomplikowanego fraktala, ale jest to przypuszczenie błędne, jak wykazała Mirzakhani w pracy wspólnej z Alexem Eskinem i Amirem Mohammadim. Odpowiedź poprawna: takie powierzchnie tworzą rozmaitość, czyli wielowymiarowy odpowiednik powierzchni, określoną układem równań liniowych. Bardziej technicznie, autorzy udowodnili The Magic Wand Conjecture (hipotezę czarodziejskiej różdżki, teraz już twierdzenie): domknięcie orbity dowolnej płaskiej powierzchni translacyjnej w 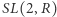 jest algebraicznym orbifoldem. Wcześniej McMullen udowodnił to dla powierzchni genusu 2.
jest algebraicznym orbifoldem. Wcześniej McMullen udowodnił to dla powierzchni genusu 2.
Dowód tego wyniku jest niezwykle trudny, a główna jego część wymaga setki stron subtelnej analizy. Mimo technicznego charakteru ma wiele zastosowań. Dostarcza, na przykład, nowych informacji o bilardzie na dowolnym wielokącie (wyobraźmy sobie stół bilardowy, którego brzeg jest jakimś wielokątem; co się dzieje z bilą, która odbija się od boków nieskończenie wiele razy?). Przykład może się wydać frywolny, jednakże dynamika bilardu ma kluczowe znaczenie w dynamice chaosu i niektórych obszarach teorii kwantów. W szczególności, niektóre trajektorie biegną po torze zamkniętym, a więc powtarzają swoje zachowanie w nieskończoność (dynamika okresowa), inne zaś są "ergodyczne" i gęsto wypełniają pewien obszar (dynamika chaosu). To rozróżnienie ma w dynamice fundamentalne znaczenie; bilard dostarcza użytecznych układów do badania takich różnic oraz przyczyn ich powstawania.
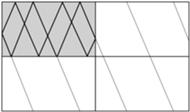
Powtarzalne odbijanie trajektorii bili (czarna linia) o brzeg stołu bilardowego (zacieniowany) przekształca ją w geodezyjną (szare linie) na dwa razy większym prostokącie z utożsamionymi przeciwległymi bokami. Geodezyjna ta jest zamknięta.
Związek z powierzchniami translacyjnymi najprościej zauważyć, gdy stół jest prostokątny. Odbijając prostokąt w odpowiednich bokach, otrzymujemy prostokąt dwa razy większy. Jeśli w ten sam sposób odbijemy trajektorię bili, powstanie zamknięta geodezyjna na powierzchni translacyjnej, otrzymanej przez utożsamienie przeciwległych boków większego prostokąta. Podobna konstrukcja działa też dla dowolnej powierzchni translacyjnej.
Kolejnym przykładem interpretacji bilarda jest problem oświetlenia pokoju: ile żarówek potrzeba, by każdy punkt danego pokoju był oświetlony? Żarówki uznajemy za punkty, promienie świetlne biegną prostoliniowo i odbijają się od ścian jak bile w bilardzie. Odpowiedź na to pytanie można zacząć od ustalenia, które części pokoju są oświetlone przez jedną żarówkę w dowolnym położeniu. Odwołując się do twierdzenia czarodziejskiej różdżki, Samuel Lelièvre, Thierry Monteil i Barak Weiss udowodnili, że w dowolnym pokoju w kształcie translacyjnego wielokąta i dowolnego położenia pojedynczej żarówki pozostawia ona tylko skończenie wiele punktów nieoświetlonych.
Maryam Mirzakhani była niezwykle uzdolnioną matematyczką, wysoce oryginalną, zdecydowaną uderzać w rzeczywiście trudne problemy uprawianej dziedziny. Jej badania połączyły ważne obszary czystej matematyki, matematyki stosowanej, fizyki matematycznej, jej nowe metody przynosiły przełom za przełomem. Nie możemy wiedzieć, co by osiągnęła, gdyby dożyła sędziwego wieku. Możemy jednak cieszyć się z pozostawionych przez nią pomysłów i twierdzeń, z bogatego matematycznego spadku, na którym budować będą następne pokolenia.
tłumaczył Wiktor BARTOL