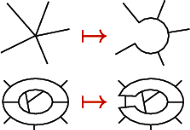
Deltoid
Kraje, stolice, granice...
Styczniowy deltoid poświęcony był dwubarwnym mapom...

Rys. 1 Np. Paragwaj, Luksemburg, województwo wielkopolskie świadczą o tym, że do pomalowania odpowiednich map nie wystarczą trzy kolory
Udowodniliśmy w nim
Twierdzenie 1. Mapę można pomalować dwoma kolorami wtedy i tylko wtedy, gdy każdy jej wierzchołek jest stopnia parzystego.
Przyjmujemy tę samą terminologię oraz założenia o mapach i ich kolorowaniach.
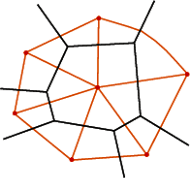
Rys. 2 Fragmenty map 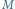 i
i 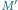

Rys. 3 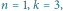 więc
więc 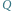 ma kolor
ma kolor 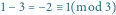

Rys. 4 Dwoma kolorowymi bokami trójkąta zastępujemy pojedynczą krawędź drogi  (trzeci bok tego trójkąta)
(trzeci bok tego trójkąta)
Ograniczmy teraz nasze rozważania do map regularnych (definicja na marginesie). W każdym wierzchołku takiej mapy schodzą się trzy kraje, z pewnością więc dwie barwy nie wystarczą do pomalowania ich. Co więcej, jeśli jakiś kraj ma nieparzystą liczbę sąsiadów, to nie da się ich pokolorować dwiema barwami (Rys. 1). Dowodzi to jednej z implikacji w poniższym twierdzeniu.
Twierdzenie 2. Mapę regularną można pomalować trzema kolorami wtedy i tylko wtedy, gdy każdy jej kraj ma parzystą liczbę sąsiadów.
W dowodzie drugiej implikacji przyda się pojęcie mapy 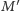 dualnej do mapy
dualnej do mapy 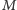 : jej wierzchołkami są stolice państw mapy
: jej wierzchołkami są stolice państw mapy 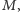 a jeśli dwa państwa sąsiadują, to w poprzek ich granicy rysujemy krawędź łączącą stolice (Rys. 2).
a jeśli dwa państwa sąsiadują, to w poprzek ich granicy rysujemy krawędź łączącą stolice (Rys. 2).
Dowód. Jeśli każdy kraj na mapie 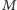 ma parzystą liczbę sąsiadów, to każdy wierzchołek mapy
ma parzystą liczbę sąsiadów, to każdy wierzchołek mapy 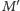 ma stopień parzysty. Na mocy twierdzenia 1 możemy więc mapę
ma stopień parzysty. Na mocy twierdzenia 1 możemy więc mapę 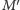 pomalować na czarno-biało. Ponadto każdy jej kraj jest trójkątem, co wynika z regularności mapy
pomalować na czarno-biało. Ponadto każdy jej kraj jest trójkątem, co wynika z regularności mapy 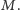 Pomalujemy wierzchołki
Pomalujemy wierzchołki 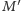 barwami 0, 1, 2.
barwami 0, 1, 2.
Pokolorujmy dowolny wierzchołek 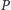 barwą 0. Następnie każdy inny wierzchołek
barwą 0. Następnie każdy inny wierzchołek 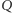 połączmy z
połączmy z 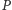 dowolnym ciągiem różnych krawędzi i pomalujmy kolorem
dowolnym ciągiem różnych krawędzi i pomalujmy kolorem 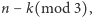 gdzie
gdzie 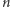 to liczba krawędzi wzdłuż tej drogi od
to liczba krawędzi wzdłuż tej drogi od 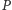 do
do 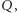 które mają czarny trójkąt po lewej stronie, a
które mają czarny trójkąt po lewej stronie, a 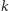 - po prawej (Rys. 3). Aby zakończyć dowód, należy wykazać, że kolor wierzchołka
- po prawej (Rys. 3). Aby zakończyć dowód, należy wykazać, że kolor wierzchołka 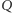 nie zależy od wyboru drogi.
nie zależy od wyboru drogi.
Rozważmy dwie różne drogi 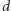 i
i 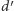 i deformujmy
i deformujmy 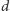 do
do 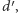 "mijając" kolejne trójkąty jak na rysunku 4 Wówczas jedną krawędź wliczaną do
"mijając" kolejne trójkąty jak na rysunku 4 Wówczas jedną krawędź wliczaną do 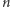 zastępujemy dwiema liczonymi do
zastępujemy dwiema liczonymi do 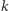 lub jedną z
lub jedną z 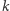 - dwiema z
- dwiema z 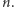 Ponieważ
Ponieważ 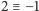 oraz
oraz 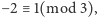 taka zmiana nie wpływa na kolor wierzchołka
taka zmiana nie wpływa na kolor wierzchołka 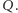 Stąd faktycznie kolor ten nie zależy od wyboru drogi, a barwy sąsiednich wierzchołków (państw mapy
Stąd faktycznie kolor ten nie zależy od wyboru drogi, a barwy sąsiednich wierzchołków (państw mapy 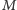 ) różnią się o 1.
) różnią się o 1.
****
Słynne twierdzenie orzeka, że każdą mapę da się pomalować najwyżej czterema barwami.
Dowodu (bardzo trudnego) nie przedstawimy, ale pokażemy równoważność pewnych warunków.
Twierdzenie 3. Mapę regularną można pomalować czterema kolorami wtedy i tylko wtedy, gdy jej krawędzie można pomalować trzema kolorami tak, by w każdym wierzchołku schodziły się krawędzie trzech różnych barw.
Dowód. Rozważmy mapę pomalowaną czterema kolorami: 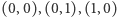 ,
, 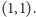 Pokolorujmy każdą z krawędzi barwą odpowiadającą sumie graniczących wzdłuż niej państw, przy czym dodawanie wykonujemy po współrzędnych i modulo 2, np.
Pokolorujmy każdą z krawędzi barwą odpowiadającą sumie graniczących wzdłuż niej państw, przy czym dodawanie wykonujemy po współrzędnych i modulo 2, np. 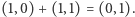 Są wówczas tylko trzy możliwe kolory krawędzi:
Są wówczas tylko trzy możliwe kolory krawędzi: 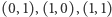 - sumy sześciu możliwych par różnych barw krajów.
- sumy sześciu możliwych par różnych barw krajów.
Zauważmy, że każda barwa zsumowana sama ze sobą daje 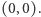 Stąd suma kolorów trzech krawędzi w każdym z wierzchołków też równa jest
Stąd suma kolorów trzech krawędzi w każdym z wierzchołków też równa jest 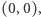 gdyż kolor każdego z państw jest w niej liczony dwukrotnie. Wobec tego dwie krawędzie jednego wierzchołka nie mogą mieć tego samego koloru, gdyż wówczas ich suma byłaby równa
gdyż kolor każdego z państw jest w niej liczony dwukrotnie. Wobec tego dwie krawędzie jednego wierzchołka nie mogą mieć tego samego koloru, gdyż wówczas ich suma byłaby równa 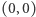 i zmieniłaby się po dodaniu trzeciej (różnej od
i zmieniłaby się po dodaniu trzeciej (różnej od 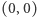 ). Uzyskaliśmy więc odpowiednie kolorowanie krawędzi.
). Uzyskaliśmy więc odpowiednie kolorowanie krawędzi.
Załóżmy teraz, że krawędzie mapy pokolorowano barwami 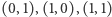 w sposób opisany w twierdzeniu. Pomalujmy dowolnie wybrany kraj
w sposób opisany w twierdzeniu. Pomalujmy dowolnie wybrany kraj 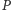 kolorem
kolorem 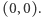 Następnie każdy inny kraj
Następnie każdy inny kraj 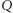 połączmy z
połączmy z 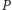 dowolną drogą nieprzechodzącą przez wierzchołki mapy i pomalujmy kolorem równym sumie barw wszystkich przekraczanych po drodze granic. Aby zakończyć dowód, należy wykazać, że kolor państwa
dowolną drogą nieprzechodzącą przez wierzchołki mapy i pomalujmy kolorem równym sumie barw wszystkich przekraczanych po drodze granic. Aby zakończyć dowód, należy wykazać, że kolor państwa 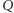 nie zależy od wyboru drogi. Rozumowanie to, bazujące na deformowaniu drogi, przebiega analogicznie do dowodu twierdzenia 1 (tym razem każdy wierzchołek ma stopień 3 i suma kolorów dwóch jego krawędzi równa jest kolorowi trzeciej). Barwy sąsiednich krajów różnią się wówczas o barwę ich granicy.
nie zależy od wyboru drogi. Rozumowanie to, bazujące na deformowaniu drogi, przebiega analogicznie do dowodu twierdzenia 1 (tym razem każdy wierzchołek ma stopień 3 i suma kolorów dwóch jego krawędzi równa jest kolorowi trzeciej). Barwy sąsiednich krajów różnią się wówczas o barwę ich granicy.
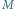 i
i 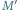
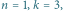 więc
więc 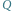 ma kolor
ma kolor 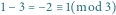
 (trzeci bok tego trójkąta)
(trzeci bok tego trójkąta)