Henryk Pawłowski
11 czerwca 2016 r. zmarł nagle Henryk Pawłowski. Był jednym z najwybitniejszych nauczycieli matematyki w kraju. Wychował wielu uczniów, był autorem cenionych zbiorów zadań olimpijskich oraz podręczników szkolnych. Prowadził kółka matematyczne w Toruniu, Poznaniu oraz Bydgoszczy, na które przyjeżdżali uczniowie z odległych miejscowości. Wielu Jego uczniów zdobyło najwyższe nagrody w Olimpiadzie Matematycznej, również w Międzynarodowej Olimpiadzie Matematycznej.

Współtworzył Olimpiadę Matematyczną Gimnazjalistów, od początku jej istnienia kierował komitetem okręgowym w Toruniu. Zapewniał wysoki poziom sprawdzania prac uczestników tych zawodów.
Był jednym z organizatorów 10 Małych Olimpiad Matematycznych, w których uczestniczyli uczniowie szkół średnich z wielu miejscowości w Polsce. Dla młodych ludzi był to nie tylko doskonały trening przed zawodami Olimpiady Matematycznej, ale też znakomita okazja do nawiązania kontaktów z rówieśnikami dzielącymi tę samą matematyczną pasję. Wielu z nich zostało laureatami Olimpiady Matematycznej i Międzynarodowej Olimpiady Matematycznej. Henryk Pawłowski organizował też lokalne zawody matematyczne w Toruniu i okolicach.
Jako nauczyciel i wychowawca zachęcał swych uczniów do myślenia zadawanymi pytaniami oraz odpowiednio dobieranymi zadaniami. Widział sens w rozwiązywaniu zadań trudnych. Wiedział, że nauczyciel powinien stawiać przed uczniem problemy na granicy jego możliwości.
Chodziło Mu przede wszystkim o intelektualny rozwój uczniów, bo doskonale rozumiał, że dobre wyniki na egzaminach są rzeczą wtórną i naturalną konsekwencją głębszych przemyśleń.
Książki Henryka z różnymi zadaniami z olimpiad stały się już klasyką wśród osób poważnie myślących o uczestnictwie w takich zawodach - dziś już trudno wyobrazić sobie przygotowania do olimpiady matematycznej bez nich. Podręczniki dla liceów, które napisał, wyróżniają się spośród innych tym, że są w nich pełne dowody twierdzeń, zadania, których rozwiązanie dostarcza zdolnym uczniom satysfakcji. Autor omawia w nich wiele twierdzeń z elementarnej matematyki, które nie są przewidziane podstawą programową, jednak są interesujące, więc uczniowie zainteresowani matematyką mają nad czym pracować. Ci, którzy z nich korzystają, są na ogół znacznie lepiej przygotowani do studiowania niż uczniowie używający książek napisanych zgodnie z panującą modą na minimalizm.
Wielokrotnie rozmawialiśmy o zadaniach. Jedną taką krótką i w miarę niedawną rozmowę chciałbym tu opowiedzieć. Henryk powiedział mi, że na jakiejś próbnej maturze pojawiło się następujące zadanie:
Zadanie. Dowieść, że jeśli ramiona 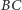 i
i 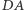 trapezu
trapezu 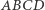 leżą na prostych prostopadłych, to
leżą na prostych prostopadłych, to 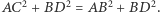
Zostało szybko rozwiązane. Mniej więcej tak. Załóżmy, że 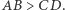 Jeśli
Jeśli 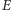 jest punktem przecięcia prostych
jest punktem przecięcia prostych 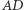 i
i 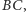 to
to

Zadanie rozwiązane. I co dalej zrobił Henryk w czasie lekcji, której część poświęcił temu zadaniu? Ano zapytał swych uczniów, w którym miejscu skorzystali z równoległości boków 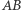 i
i 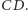 Ponieważ nie skorzystali w żadnym miejscu, więc okazało się, że twierdzenie jest prawdziwe dla każdego czworokąta. I to jeszcze nie był koniec. Padło pytanie o odwrócenie twierdzenia. Okazało się, że można odwrócić. Piszę o tym, bo bardzo mi się to podejście do zadania podoba. Ale i tak zadałem - po jakimś czasie - pytanie: a gdzie korzysta się z tego, że punkty
Ponieważ nie skorzystali w żadnym miejscu, więc okazało się, że twierdzenie jest prawdziwe dla każdego czworokąta. I to jeszcze nie był koniec. Padło pytanie o odwrócenie twierdzenia. Okazało się, że można odwrócić. Piszę o tym, bo bardzo mi się to podejście do zadania podoba. Ale i tak zadałem - po jakimś czasie - pytanie: a gdzie korzysta się z tego, że punkty 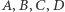 leżą w jednej płaszczyźnie? Niby korzysta się, mówiąc o przecięciu prostych
leżą w jednej płaszczyźnie? Niby korzysta się, mówiąc o przecięciu prostych 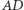 i
i 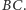 No dobrze, ale po co? Przecież można napisać, że proste
No dobrze, ale po co? Przecież można napisać, że proste 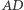 i
i 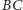 są prostopadłe (również wtedy, gdy są skośne) wtedy i tylko wtedy, gdy
są prostopadłe (również wtedy, gdy są skośne) wtedy i tylko wtedy, gdy 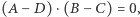 kropka oznacza iloczyn skalarny. Tę równość można przepisać w postaci
kropka oznacza iloczyn skalarny. Tę równość można przepisać w postaci 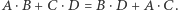 Równość, którą należało dowieść, ma postać
Równość, którą należało dowieść, ma postać 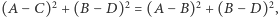 podnoszenie do kwadratu polega na mnożeniu skalarnym wektora przez siebie. Ostatnia równość jest równoważna temu, że
podnoszenie do kwadratu polega na mnożeniu skalarnym wektora przez siebie. Ostatnia równość jest równoważna temu, że 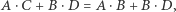 więc wywnioskowanej poprzednio z założenia. Co więcej, w ostatniej wersji dowód geometryczny zaczyna już czegoś od ucznia wymagać. Tu algebra jest rzeczywiście pomocna. A może Czytelnicy zechcą rozwiązać ostatnią wersję zadania bez algebry?
więc wywnioskowanej poprzednio z założenia. Co więcej, w ostatniej wersji dowód geometryczny zaczyna już czegoś od ucznia wymagać. Tu algebra jest rzeczywiście pomocna. A może Czytelnicy zechcą rozwiązać ostatnią wersję zadania bez algebry?
Odszedł jeden z najlepszych nauczycieli matematyki w Polsce. Henryk Pawłowski na długo pozostanie w pamięci wielu swych uczniów, czytelników swych książek, współpracowników i kolegów.