Łatwo mu mówić, bo sam zdobył Nagrodę Nobla z fizyki (co prawda do podziału z Salamem i Glashowem). Natomiast biednemu matematykowi wiatr w oczy wieje. Za Medalem Fieldsa idzie jedynie sława mołojecka (nie można go zdobyć po ukończeniu 40 lat). Czy opłaca się więc studiować matematykę? Pytanie bardzo na czasie, zwłaszcza dla tych, dla których "już za rok matura".

Czy się opłaca? To zależy dla kogo. Jeżeli ktoś np. umie naprawdę dobrze kopać piłkę, albo jeszcze lepiej okładać po... twarzy współzawodników, to może mu się studiowanie matematyki nie opłacać. Ale jeżeli wszystkie jego talenta poszły w logiczne, w abstrakcyjne myślenie, to informujemy, że opłacalność studiowania matematyki istotnie wzrosła z dniem 24 maja 2000 roku. Uczciwie trzeba jednak przyznać, że jest to opłacalność warunkowa. Samo studiowanie nie wystarczy. Trzeba jeszcze czegoś bardzo konkretnego dokonać.

Tego dnia na Spotkaniu Milenijnym odbywającym się w College de France w Paryżu, przedstawiciele Clay Mathematics Institute z Massachusetts ogłosili siedem Millennium Prize Problems. Nagroda za rozwiązanie któregokolwiek z poniższych problemów będzie - oprócz mołojeckiej sławy - okrągły milion dolarów.

• Problem P versus NP zasadza się w pytaniu, czy dla problemów, dla których istnieje dość szybki algorytm sprawdzający, czy dane rozwiązanie jest poprawne, istnieje też podobnie szybki algorytm znajdujący to rozwiązanie.
• Hipoteza Hodge'a wiąże się z próbą opisania kształtu skomplikowanych obiektów, jakie spotyka się w matematyce. Podstawowa idea opiera się na przybliżaniu kształtu danego obiektu za pomocą sklejania klocków o rosnącym wymiarze. Hipoteza Hodge'a głosi, że pewne klocki, zwane cyklami Hodge'a, dają się złożyć z pewnych innych klocków. (Aby zrozumieć, o jakie konstrukcje i o jakie klocki chodzi, należy skorzystać z rady Weinberga).
• Hipoteza Poincarego ma swoje źródło w prostej obserwacji. Jeśli na pączek mamy nałożoną gumkę recepturkę, to przesuwając ją po powierzchni pączka możemy powolutku, bez rozerwań ściągnąć ją do punktu. Z obwarzankiem nie zawsze się to uda. Poincare wiedział, że wszystkie dwuwymiarowe powierzchnie, w których każda gumka da się ściągnąć do punktu i które są w jednym kawałku oraz nie maja brzegu, wyglądają tak jak powierzchnia pączka, tzn. dają się bez rozerwań i zlepień przekształcić na sferę. Hipoteza Poincarego mówi, że trójwymiarowe powierzchnie o wymienionych wyżej cechach wyglądają tak jak trójwymiarowa sfera, czyli powierzchnia czterowymiarowej kuli.
• Hipoteza Riemanna mówi o własności tzw. funkcji 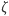Riemanna. Funkcja ta jest uogólnieniem na liczby zespolone funkcji, która każdej liczbie rzeczywistej 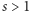przypisuje sumę odwrotności -tych potęg liczb naturalnych. Hipoteza Riemanna stwierdza, ze zera funkcji 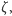które leżą w prawej półpłaszczyźnie, mają część rzeczywistą równą 1/2.
• Udowodnienie matematycznej poprawności teorii Yanga-Millsa sprowadza się do wykazania, że teoria cząstek elementarnych posługuje się matematyką.
• Znalezienie gładkich rozwiązań równania Naviera-Stokesa opisującego przepływ lepkiej cieczy. Problem to mniej więcej pytanie o to, jak znaleźć prędkość i ciśnienie płynu, gdy znamy - odpowiednio regularne - siły na niego działające.
• Hipoteza Bircha i Swinnertona-Dyera dotyczy rozwiązywania równań w liczbach całkowitych. W ogólnym przypadku nie istnieje uniwersalna metoda pozwalająca stwierdzić, czy dane równanie (o współczynnikach całkowitych) ma rozwiązanie, czy nie. Hipoteza Bircha i Swinnertona-Dyra stwierdza, że w pewnych specjalnych przypadkach da się jednak rozstrzygnąć, czy równanie ma skończenie wiele, czy też nieskończenie wiele rozwiązań.

Powyższe problemy wybrano jako ważne, klasyczne pytania, które pozostają nierozwiązane od wielu lat. Oczywiście nawiązano również do słynnego wystąpienia Davida Hilberta w dniu 8 sierpnia 1900 roku na Drugim Międzynarodowym Kongresie Matematycznym w Paryżu. Hilbert ogłosił w swoim referacie 23 otwarte problemy matematyki, które w ogromnym stopniu wytyczyły rozwój matematyki w XX wieku. Jednym z problemów przedstawionych przez Hilberta była (obecnie na nowo ńominowana") hipoteza Riemanna, która od ponad stu lat jest powszechnie uważana za jeden z najważniejszych otwartych problemów matematyki.

Intencja CMI Millennium Prize Problems nie jest, jak twierdzą fundatorzy, ukierunkowanie matematyki następnego stulecia. Chodzi raczej o zwrócenie uwagi na pewien zbiór pytań, które przez dziesiątki lat pozostają bez rozwiązania, pomimo intensywnych badań.

Ciekawa jest również zwięźle opisana szczegółowa procedura ewentualnego przyznawania nagród (niestety nie w pełni jednoznaczna). Najważniejsze jest to, że rozpatrywane będą tylko takie rozwiązania, które w dwa lata po opublikowaniu w renomowanym czasopiśmie matematycznym o światowym zasięgu będą cieszyć się powszechną akceptację środowiska matematycznego.

Bez zgody wszystkich wypracowujących decyzje osób żadne szczegóły procesu rozpatrywania rozwiązania nie będę mogły zostać ujawnione przed upływem siedemdziesięciu pięciu lat od zakończenia sprawy. Matematyka jest wieczna.