Na czym stoi matematyka?

Matematyka bardzo się w XIX wieku zmieniła. Algebra, badająca dotąd przede wszystkim metody rozwiązywania równań wielomianowych, dzięki pracom Evariste'a Galois, George'a Boole'a i innych wytworzyła struktury abstrakcyjne: grupy, pierścienie, algebry Boole'a, oderwane od obliczeń liczbowych, reprezentujące za to pewne ogólne własności działań (na dowolnych obiektach). Geometria utraciła euklidesową jednoznaczność, odnajdując się w światach dotąd nieznanych i nieprzewidywanych, zwanych geometriami nieeuklidesowymi. Analiza, nabierając coraz bardziej potrzebnej ścisłości, wyszła poza granice intuicji, uwzględniając szerszy repertuar funkcji (niegdyś uważanych za ciągłe z definicji) i dopuszczając zaskakujące konstrukcje, jak choćby funkcje wszędzie ciągłe i nigdzie nieróżniczkowalne.

W drugiej połowie XIX wieku badania Georga Cantora nad reprezentacjami funkcji za pomocą szeregów doprowadziły do otwarcia matematycznych drzwi dla starannie dotąd omijanej nieskończoności aktualnej, nieskończoności "istniejącej", danej w całości - w odróżnieniu od potencjalnej, czyli takiej, która oznacza jedynie możliwość nieograniczonego powiększania zbioru. Cantor pokazał, że można sensownie porównywać wielkości zbiorów nieskończonych, operować nimi tak, jakby były dobrze określonymi obiektami matematycznymi.

Niestety, okazało się, że pojęcie zbioru (w szczególności nieskończonego) dobrze określone nie było. Bertrand Russell wskazał na sprzeczność wyrosłą z nieprecyzyjnego rozumienia zbioru. Istotnie, jeśli możemy dowolnie tworzyć zbiory, to w szczególności możemy utworzyć zbiór 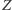$Z$ wszystkich tych zbiorów, które nie są swoimi własnymi elementami. Inaczej mówiąc, 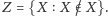$|Z = {X X /∈ X}.$ Próba odpowiedzi na pytanie, czy 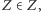$Z ∈ Z,$ jak nietrudno stwierdzić, prowadzi do sprzeczności. Nieco wcześniej, pod koniec XIX wieku, Cesare Burali-Forti pokazał, że nie istnieje, że nie można utworzyć zbioru wszystkich liczb porządkowych. Sprzeczności tego rodzaju pojawiły się także w logice. Czy zatem swoboda używania nader abstrakcyjnych pojęć, w tym nieskończoności aktualnej, powinna być matematykom odebrana?

Zagrożenie pojawieniem się sprzeczności wywołało różne reakcje w środowisku matematycznym. Leopold Kronecker zaproponował, by za fundament matematyki przyjąć liczby naturalne, unikając w ten sposób wszystkiego, czego nie da się z nich wyprowadzić. Wielu matematyków gotowych było zrezygnować z tej części matematyki, która dopuszczała zbiory aktualnie nieskończone, a nawet ze wszystkiego, czego nie dawało się konstruktywnie pokazać (nie tylko wykazać). Intuicjoniści, jak określa się zwolenników jednej z takich konstruktywistycznych filozofii, nie uznawali tzw. prawa wyłączonego środka, czyli uznawali zdanie "a lub nie a" za prawdziwe wtedy, gdy udowodniło się a lub udowodniło nie a; o porównywaniu zbiorów nieskończonych nie było mowy. Przyjęcie takiego punktu widzenia oznaczałoby utratę wielu ważnych twierdzeń.

David Hilbert, wybitny niemiecki matematyk przełomu wieków XIX i XX, autor przedstawionych w 1900 roku na II Międzynarodowym Kongresie Matematyków 23 problemów, które miały wytyczyć kierunki rozwoju matematyki w XX wieku, nie godził się z takim okrojeniem matematyki. Zaproponował sposób działania, który mógłby przeciąć wszelkie wątpliwości, a jednocześnie pozwoliłby pozostać w, jak to określił, "raju Cantora", czyli w świecie bezpiecznej nieskończoności.

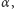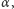Na czym polegał ten sposób, nazwany programem Hilberta? Przede wszystkim na uczynieniu z teorii matematycznych przedmiotu badań, w efekcie których można byłoby udowodnić kilka pożądanych ich cech, przede wszystkim niesprzeczność i zupełność. Teoria jest niesprzeczna, gdy nie istnieje takie zdanie $|α,$ że i $α ,$ i negacja 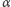$α$ są twierdzeniami teorii (równoważnie, gdy istnieje zdanie niemające dowodu). Teoria jest zupełna, gdy każde zdanie prawdziwe w dowolnym modelu teorii jest jej twierdzeniem, a więc istnieje dla niego dowód wychodzący od aksjomatów (równoważnie, gdy dla każdego zdania 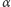$|α$ jest tak, że albo 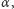$|α,$ albo negacja 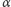$|α$ jest twierdzeniem tej teorii).

Pierwszym krokiem do badania teorii matematycznej jest jej sformalizowanie, a więc: określenie zbiorów symboli reprezentujących obiekty, którymi teoria ma się zajmować, symboli logicznych, symboli reprezentujących działania na obiektach i relacje między nimi, ścisła identyfikacja uznawanych za poprawne wyrażeń zapisanych za pomocą tych symboli, wybór niektórych wyrażeń i uznanie ich za niezbędny początek każdego dowodu (aksjomaty) oraz dokładny opis reguł przetwarzania wyrażeń (reguły wnioskowania). Oczywiście, samo pojęcie dowodu musi być równie ściśle zdefiniowane jako pewien ciąg wyrażeń, w którym każde jest albo aksjomatem, albo jest skutkiem zastosowania reguły wnioskowania do wcześniejszych wyrażeń.

Do tak sformalizowanej teorii można zastosować metody matematyczne i wykazać owe dobre własności. Hilbert pisał o metodach "finitystycznych", nie precyzując dokładnie znaczenia tego terminu; chodziło o metody wymagające "skończenie wielu kroków". Od takich metod należałoby wymagać zachowawczości, co oznacza, że gdy zredukujemy je do zbiorów skończonych - choć obejmować mają wszystkie - to tak uzyskane wnioski będą zgodne z tym, co o zbiorach skończonych już wiemy.

Próbę takiej konstrukcji matematyki podjęli Bertrand Russell i Alfred North Whitehead w publikowanym w latach 1910-1913 (choć niedokończonym) dziele Principia Mathematica. Cóż... Kilkanaście lat później, w 1931 roku, ukazała się praca Kurta Friedricha Gödla Über formal unenstcheidbare Sätze der Principia Mathematica und verwandter Systeme I (O formalnie nierozstrzygalnych zdaniach Principia Mathematica i podobnych systemów I). Gödel udowodnił w niej m.in. dwa kluczowe dla sprawy twierdzenia. Po pierwsze, dla każdej dostatecznie bogatej (dokładniej, takiej, w której można wyrazić arytmetykę liczb naturalnych) niesprzecznej teorii matematycznej istnieje zdanie 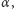$|α,$ takie że ani 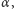$α ,$ ani negacja 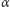$α$ nie jest twierdzeniem tej teorii. Inaczej mówiąc, nie można w takich przypadkach osiągnąć zupełności. A po drugie - wniosek z pierwszego twierdzenia - metodami takiej teorii nie można udowodnić jej niesprzeczności. Innymi słowy, aby udowodnić niesprzeczność pewnej teorii, trzeba wyjść poza nią i użyć środków teorii bogatszej. Skąd jednak pewność, że bogatsza teoria jest niesprzeczna? Trzeba jeszcze bogatszej teorii... Matematyka funkcjonuje zatem w warunkach, które można określić jako niesprzeczność warunkowa.

Program Hilberta pozostał więc nierealizowalną mrzonką. Trudno jednak obarczać Davida Hilberta winą za to niepowodzenie. Jego oczekiwania wydawały się tak naturalne... A matematyka wzbogaciła się o dwie nowe dyscypliny: metamatematykę i teorię dowodu, a także o twierdzenia Gödla, które można z pewną swobodą językową określić jako "kultowe".