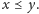Złoty podział w sortowaniu
Złoty podział odcinka, zwany też złotą proporcją, jest doskonale znany. Okazuje się, że podobną własność można sformułować dla problemu sortowania...
Definicja. Niech
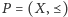 będzie zbiorem częściowo uporządkowanym,
czyli zbiorem
będzie zbiorem częściowo uporządkowanym,
czyli zbiorem
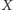 wyposażonym w relację częściowego porządku
wyposażonym w relację częściowego porządku
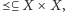 spełniającą warunki:
spełniającą warunki:
- (zwrotność)
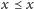 dla każdego
dla każdego
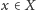 ;
;
- (przechodniość) jeśli
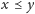 i
i
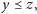 to
to
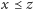 dla każdych
dla każdych
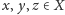 ;
;
- (antysymetryczność) jeśli
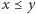 i
i
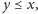 to
to
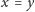 dla każdych
dla każdych
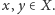
Definicja. Zbiorem liniowo uporządkowanym nazywamy zbiór częściowo uporządkowany, w którym każde dwa elementy są porównywalne, czyli spełniony jest dodatkowy warunek:
- (spójność)
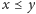 lub
lub
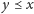 dla każdych
dla każdych
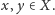
Definicja. Rozszerzeniem liniowym
zbioru częściowo uporządkowanego
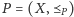 nazywamy każdy
zbiór liniowo uporządkowany
nazywamy każdy
zbiór liniowo uporządkowany
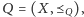 który zachowuje relację
porządku, czyli
który zachowuje relację
porządku, czyli
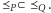 Rozszerzenie liniowe utożsamiamy
z permutacją elementów zbioru
Rozszerzenie liniowe utożsamiamy
z permutacją elementów zbioru
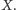
W dalszym ciągu będziemy rozważać tylko zbiory skończone. Dla przykładu
niech
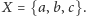 Totalnym nieporządkiem na tym zbiorze jest zbiór
częściowo uporządkowany
Totalnym nieporządkiem na tym zbiorze jest zbiór
częściowo uporządkowany
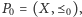 taki że nie zachodzi
taki że nie zachodzi
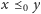 dla dowolnych różnych
dla dowolnych różnych
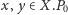 ma sześć
rozszerzeń liniowych:
ma sześć
rozszerzeń liniowych:
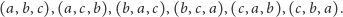 |
Sortowanie zbioru częściowo uporządkowanego polega na zadawaniu
pytań o relację między jego elementami w celu wybrania jednego z jego
rozszerzeń liniowych. Niech
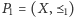 będzie zbiorem częściowo
uporządkowanym, który chcemy posortować. Jeśli na pytanie o elementy
będzie zbiorem częściowo
uporządkowanym, który chcemy posortować. Jeśli na pytanie o elementy
 i
i
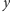 uzyskamy odpowiedź, że
uzyskamy odpowiedź, że
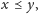 to rozszerzamy
relację
to rozszerzamy
relację
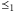 o tę informację. Wynikiem jest nowa relacja
o tę informację. Wynikiem jest nowa relacja
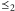 i nowy
zbiór częściowo uporządkowany
i nowy
zbiór częściowo uporządkowany
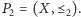 Formalnie relacja
Formalnie relacja
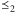 jest domknięciem przechodnim relacji
jest domknięciem przechodnim relacji
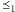 uzupełnionej
o porównanie
uzupełnionej
o porównanie
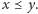
Definicja. Domknięcie przechodnie relacji dwuargumentowej
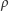 na
zbiorze
na
zbiorze
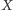 jest to najmniejsza (w sensie inkluzji) relacja przechodnia
jest to najmniejsza (w sensie inkluzji) relacja przechodnia
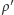 na zbiorze
na zbiorze
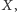 taka że
taka że
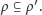
Sortowanie kończy się, gdy w wyniku zadawania kolejnych pytań
otrzymamy zbiór liniowo uporządkowany. Oczywiście, nie ma sensu
zadawanie pytania, na które znamy odpowiedź, czyli pytania o relację między
elementami
 i
i
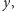 jeśli
jeśli
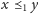 lub
lub
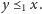 Dla
zachowania ścisłości przyjmujemy, że po zadaniu takiego pytania relacja nie
zmienia się.
Dla
zachowania ścisłości przyjmujemy, że po zadaniu takiego pytania relacja nie
zmienia się.
Wróćmy do naszego przykładu trójelementowego zbioru
 i totalnego
nieporządku na nim. Chcąc go posortować, możemy zadać pytanie o relację
między elementami
i totalnego
nieporządku na nim. Chcąc go posortować, możemy zadać pytanie o relację
między elementami
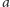 i
i
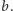 Jeśli odpowiedzią jest
Jeśli odpowiedzią jest
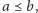 to
nadal możliwe są rozszerzenia liniowe
to
nadal możliwe są rozszerzenia liniowe
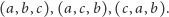 |
Jeśli natomiast odpowiedź brzmi
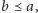 to pozostają rozszerzenia
liniowe
to pozostają rozszerzenia
liniowe
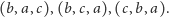 |
Zauważmy, że wykonanie porównania dzieli zbiór rozszerzeń liniowych na
dwa rozłączne podzbiory. Niech
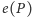 oznacza liczbę rozszerzeń
liniowych zbioru częściowo uporządkowanego. Łatwo zauważyć,
że dla dowolnego zbioru częściowo uporządkowanego
oznacza liczbę rozszerzeń
liniowych zbioru częściowo uporządkowanego. Łatwo zauważyć,
że dla dowolnego zbioru częściowo uporządkowanego
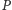 jeśli
jeśli
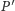 i
i
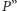 oznaczają rozszerzenie
oznaczają rozszerzenie
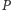 odpowiednio o warunek
odpowiednio o warunek
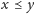 i
i
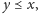 to
to
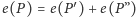 i przynajmniej
jedna z wartości
i przynajmniej
jedna z wartości
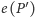 lub
lub
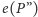 jest nie mniejsza niż
jest nie mniejsza niż
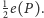
Zastanówmy się, jaka jest minimalna liczba porównań
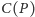 potrzebna
i zawsze wystarczająca do posortowania danego zbioru częściowo
uporządkowanego
potrzebna
i zawsze wystarczająca do posortowania danego zbioru częściowo
uporządkowanego
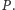 Gdyby było tak, jak w powyższym przykładzie, że
zawsze możemy podzielić zbiór rozszerzeń liniowych na równoliczne
podzbiory, to wystarczyłoby
Gdyby było tak, jak w powyższym przykładzie, że
zawsze możemy podzielić zbiór rozszerzeń liniowych na równoliczne
podzbiory, to wystarczyłoby
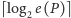 porównań. Niestety, nie
zawsze jest to możliwe. Rozważany przykład pokazuje, że możemy
uzyskać trójelementowy zbiór rozszerzeń liniowych i wtedy najlepszy
możliwy do uzyskania podział jest w stosunku
porównań. Niestety, nie
zawsze jest to możliwe. Rozważany przykład pokazuje, że możemy
uzyskać trójelementowy zbiór rozszerzeń liniowych i wtedy najlepszy
możliwy do uzyskania podział jest w stosunku
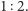 Okazuje się, że
najprawdopodobniej jest to przypadek najbardziej pesymistyczny. Mówi o tym
hipoteza
Okazuje się, że
najprawdopodobniej jest to przypadek najbardziej pesymistyczny. Mówi o tym
hipoteza
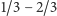 sformułowana wiele lat temu niezależnie przez
Kislicyna, Fredmana i Liniala.
sformułowana wiele lat temu niezależnie przez
Kislicyna, Fredmana i Liniala.
Hipoteza 1. Dla dowolnego skończonego zbioru częściowo uporządkowanego
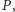 który nie jest liniowo uporządkowany, zawsze możemy wskazać dwa
elementy, takie że w wyniku ich porównania (niezależnie od wyniku tego
porównania) otrzymujemy rozszerzenie
który nie jest liniowo uporządkowany, zawsze możemy wskazać dwa
elementy, takie że w wyniku ich porównania (niezależnie od wyniku tego
porównania) otrzymujemy rozszerzenie
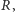 dla którego zachodzi
dla którego zachodzi
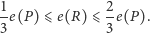 |
Powyższą hipotezę udowodniono dla wielu przypadków szczególnych, co
pozwala wierzyć w jej prawdziwość. Jednak w ogólnym przypadku nadal
pozostaje jednym z ważniejszych problemów otwartych teorii zbiorów
częściowo uporządkowanych. Prawdziwość tej hipotezy implikuje
możliwość posortowania zbioru częściowo uporządkowanego
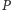 za
pomocą maksymalnie
za
pomocą maksymalnie
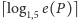 porównań (przypomnijmy, że
porównań (przypomnijmy, że
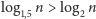 dla
dla
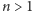 ).
).
Czy można lepiej? Wydaje się, że tak. Autor tego artykułu sformułował kilka lat temu hipotezę złotego podziału dla zbiorów częściowo uporządkowanych.
Hipoteza 2. Dla dowolnego skończonego zbioru częściowo uporządkowanego
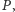 który nie jest liniowo uporządkowany, zawsze możemy wskazać dwa
kolejne porównania, takie że niezależnie od ich wyniku otrzymujemy kolejno
rozszerzenia
który nie jest liniowo uporządkowany, zawsze możemy wskazać dwa
kolejne porównania, takie że niezależnie od ich wyniku otrzymujemy kolejno
rozszerzenia
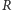 i
i
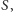 dla których zachodzi
dla których zachodzi
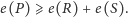 |
Hipoteza złotego podziału jest bardziej ogólna od hipotezy
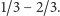 Innymi słowy, prawdziwość hipotezy złotego podziału
implikuje prawdziwość hipotezy
Innymi słowy, prawdziwość hipotezy złotego podziału
implikuje prawdziwość hipotezy
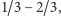 gdyż każdy kontrprzykład
dla hipotezy
gdyż każdy kontrprzykład
dla hipotezy
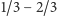 jest również kontrprzykładem dla hipotezy
złotego podziału. Załóżmy, że
jest również kontrprzykładem dla hipotezy
złotego podziału. Załóżmy, że
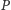 jest kontrprzykładem dla hipotezy
jest kontrprzykładem dla hipotezy
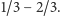 Wtedy dla każdego porównania na
Wtedy dla każdego porównania na
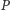 jeden z jego
wyników daje nierówność
jeden z jego
wyników daje nierówność
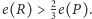 Oczywiście, dla
każdego porównania na
Oczywiście, dla
każdego porównania na
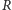 możemy wskazać jego wynik, taki że
możemy wskazać jego wynik, taki że
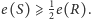 Stąd
Stąd
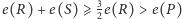 i otrzymaliśmy
kontrprzykład dla hipotezy złotego podziału.
i otrzymaliśmy
kontrprzykład dla hipotezy złotego podziału.
Jak można się domyślić, hipotezy złotego podziału również nie udało się udowodnić w ogólności, ale dowiedziono jej w tak wielu przypadkach szczególnych, że mamy podstawy, aby wierzyć w jej prawdziwość.
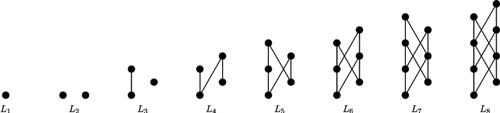
Zmierzając do finału, zobaczmy dwa proste twierdzenia, które uzasadniają
nazwę hipotezy. Niech
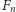 będzie
będzie
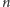 -tą liczbą Fibonacciego,
rozpoczynając od
-tą liczbą Fibonacciego,
rozpoczynając od
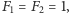 a
a
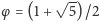 stałą złotej
proporcji.
stałą złotej
proporcji.
Dowód. Dowód prowadzimy przez indukcję. Dla
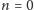 z założenia
wynika, że
z założenia
wynika, że
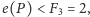 czyli zbiór
czyli zbiór
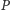 ma tylko jedno
rozszerzenie liniowe, więc jest już posortowany. Dla
ma tylko jedno
rozszerzenie liniowe, więc jest już posortowany. Dla
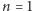 zachodzi
zachodzi
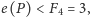 czyli
czyli
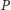 ma co najwyżej dwa rozszerzenia liniowe,
które można rozróżnić jednym porównaniem.
ma co najwyżej dwa rozszerzenia liniowe,
które można rozróżnić jednym porównaniem.
Załóżmy teraz, że twierdzenie jest prawdziwe dla
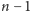 i
i
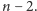 Niech
Niech
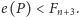 Wybieramy dwa porównania, aby spełnić nierówność
Wybieramy dwa porównania, aby spełnić nierówność
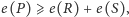 gdzie
gdzie
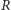 i
i
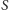 oznaczają zbiory częściowo
uporządkowane otrzymane odpowiednio po pierwszym i drugim porównaniu.
Z własności liczb Fibonacciego wynika, że zachodzi przynajmniej jedna
z nierówności
oznaczają zbiory częściowo
uporządkowane otrzymane odpowiednio po pierwszym i drugim porównaniu.
Z własności liczb Fibonacciego wynika, że zachodzi przynajmniej jedna
z nierówności
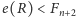 lub
lub
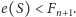 Z założenia
indukcyjnego w pierwszym przypadku możemy posortować
Z założenia
indukcyjnego w pierwszym przypadku możemy posortować
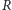 za
pomocą co najwyżej
za
pomocą co najwyżej
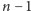 porównań, a w drugim posortować
porównań, a w drugim posortować
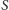 za pomocą co najwyżej
za pomocą co najwyżej
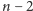 porównań. Zatem w obu
przypadkach możemy dokończyć sortowanie
porównań. Zatem w obu
przypadkach możemy dokończyć sortowanie
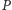 tak, aby nie
przekroczyć
tak, aby nie
przekroczyć
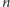 porównań.
porównań.
W powyższym twierdzeniu kres górny jest po wszystkich skończonych
zbiorach częściowo uporządkowanych, których dotyczy hipoteza złotego podziału,
czyli skończonych i nieuporządkowanych liniowo. Niech
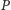 będzie takim
zbiorem częściowo uporządkowanym. Niech
będzie takim
zbiorem częściowo uporządkowanym. Niech
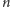 będzie liczbą porównań
wymaganych do jego posortowania (
będzie liczbą porównań
wymaganych do jego posortowania (
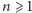 i nie można go posortować
za pomocą
i nie można go posortować
za pomocą
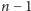 porównań). Z poprzedniego twierdzenia wynika, że
porównań). Z poprzedniego twierdzenia wynika, że
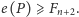 Wiadomo, że ciąg Fibonacciego spełnia nierówność
Wiadomo, że ciąg Fibonacciego spełnia nierówność
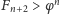 dla
dla
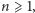 zatem
zatem
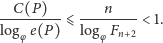 |
Linial wskazał ciąg zbiorów częściowo uporządkowanych
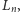 nazywanych
drabinami, takich że
nazywanych
drabinami, takich że
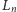 ma
ma
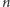 elementów,
elementów,
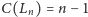 oraz
oraz
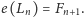 Rysunek poniżej pokazuje diagramy Hassego kilku
początkowych zbiorów
Rysunek poniżej pokazuje diagramy Hassego kilku
początkowych zbiorów
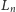 i pozwala odgadnąć regułę ich konstrukcji
oraz genezę ich nazwy.
i pozwala odgadnąć regułę ich konstrukcji
oraz genezę ich nazwy.
Ponieważ
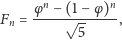 |
więc mamy
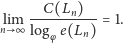 |
Z powyższych rozważań wnioskujemy, że postulowanego ograniczenia
tego
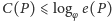 nie da się już poprawić. Równość
zachodzi wtedy i tylko wtedy, gdy
nie da się już poprawić. Równość
zachodzi wtedy i tylko wtedy, gdy
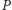 jest liniowo uporządkowany
– wtedy
jest liniowo uporządkowany
– wtedy
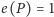 i
i
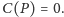 Zauważmy też, że
Zauważmy też, że
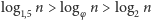 dla
dla
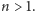 Nieco nieformalnie można
powiedzieć, że podczas sortowania każde porównanie może zmniejszyć
średnio liczbę rozszerzeń liniowych przynajmniej o współczynnik
złotej proporcji. Tak właśnie jest dla drabin. Chcąc posortować drabinę
Nieco nieformalnie można
powiedzieć, że podczas sortowania każde porównanie może zmniejszyć
średnio liczbę rozszerzeń liniowych przynajmniej o współczynnik
złotej proporcji. Tak właśnie jest dla drabin. Chcąc posortować drabinę
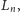 należy porównać dwa jej elementy maksymalne. W wyniku zbiór
jej rozszerzeń liniowych o liczności
należy porównać dwa jej elementy maksymalne. W wyniku zbiór
jej rozszerzeń liniowych o liczności
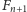 zostaje podzielony na dwa
podzbiory o liczności odpowiednio
zostaje podzielony na dwa
podzbiory o liczności odpowiednio
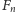 i
i
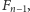 a problem
redukuje się do posortowania odpowiednio drabiny
a problem
redukuje się do posortowania odpowiednio drabiny
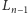 lub
lub
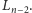
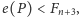
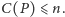
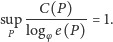
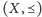 za pomocą grafu nieskierowanego. Elementy
przedstawia się jako węzły, a relacje między elementami zaznacza się, łącząc
te węzły krawędziami. Przy czym rysuje się tylko niezbędne krawędzie.
Jeśli
za pomocą grafu nieskierowanego. Elementy
przedstawia się jako węzły, a relacje między elementami zaznacza się, łącząc
te węzły krawędziami. Przy czym rysuje się tylko niezbędne krawędzie.
Jeśli
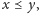 to element
to element
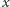 rysuje się niżej niż element
rysuje się niżej niż element
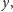 a krawędź między nimi rysuje się tylko wtedy, gdy nie istnieje taki
element
a krawędź między nimi rysuje się tylko wtedy, gdy nie istnieje taki
element
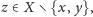 że
że
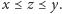
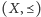 jest to taki element
jest to taki element
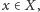 że nie istnieje element
że nie istnieje element
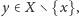 dla którego
dla którego