Potem zacząłem szukać argumentów za nieskończonością. W teorii liczb szukamy nieskończenie wielu liczb pierwszych bliźniaczych. W analizie mówimy o ciągach zbieżnych. Wiele twierdzeń o istnieniu jest prawdziwych tylko w przestrzeniach zupełnych, które trudno zdefiniować bez nieskończoności.

Ale co by było, gdyby nieskończoność zamienić na jakąś dużą liczbę, np.

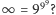
Przecież w obserwowalnym wszechświecie jest tylko skończona liczba atomów. Na prostej jest „fizycznie” tylko skończona ilość punktów. Rachunki robione za pomocą komputerów są skończone, dalekie od powyższej nieskończoności, a coraz częściej się na nich opieramy.

Jeśli chcemy coś udowodnić dla tak dużych liczb, musimy nadal korzystać z indukcji matematycznej. W topologii bardzo wiele problemów sprowadza się do obiektów kawałkami liniowych, które są określone przez skończoną ilość danych.

W końcu skłaniam się ku stwierdzeniu, że nieskończoność nie jest bardzo ważna, ale nie wypędzałbym jej całkowicie, dałbym jej żyć na uboczu, choćby ze względu na teorię zbiorów, która bez nieskończoności i bez różnych mocy i porządków strasznie by zubożała. Też najróżniejsze kontrprzykłady, które pozwalają lepiej zrozumieć matematykę, są bardzo często oparte na nieskończoności.

Mniej więcej tak napisałbym pół roku temu. Może dodałbym jeszcze kilka przykładów za i przeciw nieskończoności. Ale pół roku temu zacząłem zajmować się problemem średniowalności (amenability) dla niektórych grup skończenie generowanych.

Próbuję rozstrzygnąć, czy dla danej grupy 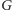istnieje miara skończona, skończenie addytywna, która jest określona dla wszystkich podzbiorów grupy 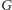i jest niezmiennicza ze względu na przesunięcia z lewej strony (to znaczy gdy mnożymy wszystkie elementy podzbioru 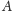z lewej strony przez dowolny ustalony element grupy 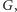 to miara nowego zbioru jest taka jak miara zbioru ).

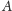Dla grup skończonych wystarczy wziąć ilość elementów 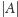 zbioru 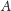 jako jego miarę.

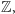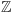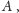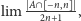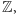Dla grup nieskończonych, na przykład dla  problem jest trudny. Dla byłoby naturalne wziąć gęstość zbioru  to znaczy  ale nie każdy zbiór ma gęstość, granica może nie istnieć, a górna granica nie jest addytywna. Żeby udowodnić istnienie takiej miary na  musimy korzystać z ultrafiltrów, w szczególności z lematu Zorna–Kuratowskiego.

Zafascynował mnie ten problem (choć jest on dosyć daleki od tego, czym się zwykle zajmuję) i wielu innych matematyków zajmuje się tym problemem od wielu lat, a bez nieskończoności problem by nie istniał.

Oczywiście, można zapytać, po co zajmować się takim problemem? Wtedy życie nieskończoności znów zawisłoby na włosku. Ale ja nie rozważam pytania, czy nieskończoność potrzebna jest „zwykłym ludziom”, tylko czy potrzebna jest matematykom, na przykład mnie. Dla matematyka fascynacja problemem jest bardzo dobrym powodem, żeby się nim zajmować. Więc głosuję TAK:

nieskończoność jest potrzebna.