Konferencja w Ameliówce
W dniach 4–6 listopada 2011 roku w hotelu Ameliówka koło Kielc odbyła się konferencja organizowana przez SEM wspólnie z Wydziałami Matematyki i Nauk Informacyjnych Politechniki Warszawskiej i Matematyki, Informatyki i Mechaniki Uniwersytetu Warszawskiego. Było to już czwarte spotkanie naukowe zorganizowane w podobnej formie przez nasze Stowarzyszenie.
Konferencja ta, podobnie jak poprzednie: Konkursy matematyczne w Polsce, Matematyka – jak uczyć? oraz Gdzie jest matematyka?, stworzyła okazję do spotkania wielu osób zainteresowanych rozbudzaniem matematycznych zdolności młodzieży.
Do Ameliówki przyjechało prawie 140 matematyków z całej Polski na co dzień zajmujących się szeroko rozumianą edukacją matematyczną. Zgodnie z tradycją uczestnikami konferencji byli zarówno nauczyciele matematyki w szkołach różnych typów, jak i pracownicy naukowi wyższych uczelni.
W trakcie konferencji odbywającej się pod hasłem Gdzie jest nauczyciel? zastanawiano się przede wszystkim nad rolą nauczyciela w kształceniu matematycznym. Próbowano odpowiedzieć na pytanie, jaką wartość wnosi nauczyciel do wykształcenia młodych ludzi. Doświadczeni nauczyciele matematyki, pracujący w specjalnych klasach matematycznych, dzielili się swoimi spostrzeżeniami i metodami pracy, pokazując Gdzie jest nauczyciel w klasie uczniów zdolnych? Dyskutowano również o podręcznikach matematyki oraz o sposobach i potrzebie uczenia matematyki humanistów. Przedstawiono także wiele interesujących zagadnień matematycznych, które można wykorzystać na zajęciach pozalekcyjnych w gimnazjach i szkołach ponadgimnazjalnych. Konferencja była też okazją prezentacji nowej formy organizacji Olimpiady Matematycznej Gimnazjalistów. Więcej informacji o konferencji można znaleźć na stronie internetowej sem.edu.pl/konferencja-2011.
Jednym z wielu bardzo ciekawych odczytów matematycznych było wystąpienie Wojciecha Martysa o inwersji względem okręgu. Chcielibyśmy zwrócić uwagę naszych Czytelników na pewną ładną własność inwersji przedstawioną wraz z dowodem podczas tego referatu.
Twierdzenie.
Niech
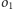 i
i
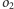 będą rozłącznymi okręgami leżącymi na danej
płaszczyźnie. Wtedy istnieje inwersja tej płaszczyzny przekształcająca okręgi
będą rozłącznymi okręgami leżącymi na danej
płaszczyźnie. Wtedy istnieje inwersja tej płaszczyzny przekształcająca okręgi
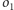 i
i
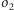 na okręgi koncentryczne.
na okręgi koncentryczne.
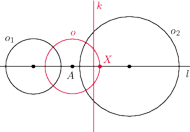
Dowód. Możemy założyć, że okręgi
 i
i
 nie są
koncentryczne. Oznaczmy przez
nie są
koncentryczne. Oznaczmy przez
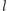 prostą przechodzącą
przez środki
prostą przechodzącą
przez środki
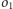 i
i
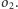 Na prostej
Na prostej
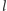 znajdujemy punkt
znajdujemy punkt
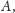 z którego długości odcinków stycznych, poprowadzonych do
z którego długości odcinków stycznych, poprowadzonych do
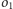 i
i
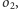 są jednakowe. Oznaczmy przez
są jednakowe. Oznaczmy przez
 długość
odcinka stycznego poprowadzonego z
długość
odcinka stycznego poprowadzonego z
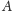 do
do
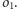 Zauważamy,
że okrąg
Zauważamy,
że okrąg
 o środku w punkcie
o środku w punkcie
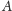 i promieniu
i promieniu
 jest prostopadły do
jest prostopadły do
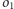 i do
i do
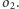 Oznaczmy przez
Oznaczmy przez
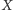 jeden z punktów przecięcia
jeden z punktów przecięcia
 z
z
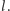 Wtedy inwersja
o środku w punkcie
Wtedy inwersja
o środku w punkcie
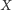 przekształca prostą
przekształca prostą
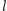 w siebie, co
oznacza, że środki obrazów
w siebie, co
oznacza, że środki obrazów
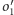 i
i
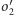 okręgów
okręgów
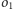 i
i
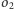 w tej inwersji leżą na
w tej inwersji leżą na
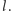 Ponadto
inwersja o środku w punkcie
Ponadto
inwersja o środku w punkcie
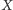 przekształca
przekształca
 na prostą
na prostą
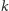 (bo
(bo
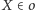 ) prostopadłą do
) prostopadłą do
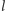 (inwersja zachowuje
kąty). Więc
(inwersja zachowuje
kąty). Więc
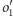 i
i
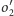 są okręgami prostopadłymi do
są okręgami prostopadłymi do
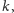 co
oznacza, że ich środki leżą na
co
oznacza, że ich środki leżą na
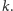 Podsumowując: środki
Podsumowując: środki
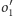 i
i
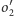 leżą na
leżą na
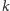 i na
i na
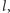 a więc
a więc
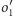 i
i
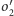 muszą być koncentryczne.
muszą być koncentryczne.
Proponujemy Czytelnikom wykorzystanie udowodnionej własności w analizie następujących zadań.