Stowarzyszenie na rzecz Edukacji Matematycznej
Nowa formuła Olimpiady Matematycznej Gimnazjalistów
W bieżącym roku szkolnym VII Olimpiada Matematyczna Gimnazjalistów została przeprowadzona w nowej, eksperymentalnej formule. Zawody stopnia pierwszego, odbywające się dotychczas wyłącznie w systemie korespondencyjnym, zostały rozbudowane o część testową, w której wzięło udział ponad 14000uczniów z 1270 szkół.
Zmiana formuły przyniosła nie tylko duże zainteresowanie samym testem, lecz także wpłynęła znacząco na zwiększenie liczby uczestników z części korespondencyjnej, a więc na zainteresowanie OMG w stałej, wypracowanej formule. Nowe elementy OMG okazały się atrakcyjne nie tylko dla uczniów w Polsce: w zawodach OMG uczestniczyły trzy polskie szkoły z Wilna. Nowością był także udział Gimnazjum nr 68 z Krakowa, będącego częścią ośrodka szkolno-wychowawczego dla dzieci niewidomych i słabowidzących. Uczniowie tej placówki zmagali się z brajlowską wersją zadań testowych.
Test składał się z 15 zadań zamkniętych i sprawdzał przede wszystkim
predyspozycje ucznia w kierunku umiejętności logicznego wyciągania
wniosków i posługiwania się podstawowymi pojęciami matematycznymi.
Każde zadanie testowe składało się z trzech stwierdzeń, a uczeń miał
podać jedynie odpowiedź, czy dane stwierdzenie jest prawdziwe. Jeśli
uczestnik udzielił trzech poprawnych odpowiedzi w obrębie jednego zadania,
otrzymywał 1 punkt, dwie poprawne odpowiedzi były warte
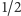 punktu.
W pozostałych przypadkach uczeń nie otrzymywał punktów. Nieudzielenie
odpowiedzi było traktowane jak udzielenie odpowiedzi błędnej.
punktu.
W pozostałych przypadkach uczeń nie otrzymywał punktów. Nieudzielenie
odpowiedzi było traktowane jak udzielenie odpowiedzi błędnej.
Taki sposób przyznawania punktów stał się pretekstem do stosowania różnych strategii. Jedno z zadań testu brzmiało:
Zadanie (4). Towar
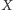 podrożał o
podrożał o
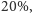 a towar
a towar
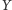 podrożał
o
podrożał
o
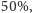 w efekcie czego oba towary kosztują tyle samo. Wynika z tego, że
przed podwyżką
w efekcie czego oba towary kosztują tyle samo. Wynika z tego, że
przed podwyżką
- a)
- towar
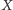 był o
był o
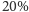 droższy od towaru
droższy od towaru
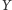 ;
;
- b)
- towar
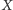 był o
był o
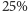 droższy od towaru
droższy od towaru
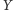 ;
;
- c)
- towar
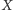 był o
był o
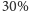 droższy od towaru
droższy od towaru
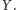
W zadaniu tym, oczywiście, co najwyżej jedna odpowiedź jest
poprawna. Nie mając pojęcia która, można strzelać — w dobrą odpowiedź
trafimy wtedy z prawdopodobieństwem
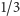 (zakładając jednak, że
układający test nie byli złośliwi i nie podali trzech błędnych wyników).
Zatem lepsza w takiej sytuacji wydaje się strategia deterministyczna: zaznaczenie
wszystkich odpowiedzi jako „Nie” gwarantuje otrzymanie co najmniej
(zakładając jednak, że
układający test nie byli złośliwi i nie podali trzech błędnych wyników).
Zatem lepsza w takiej sytuacji wydaje się strategia deterministyczna: zaznaczenie
wszystkich odpowiedzi jako „Nie” gwarantuje otrzymanie co najmniej
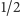 punktu.
punktu.
Nietrudno obliczyć, że wartość oczekiwana sumy uzyskanych punktów
w teście równa się niecałe
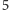 punktów.
punktów.
Średnia uzyskanych ocen w całym kraju wyniosła 6,2 punktów. Oznacza to, że test był dość trudny.
Najmniej poprawnych odpowiedzi (niecałe
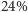 ) padło w podpunkcie b)
następującego zadania:
) padło w podpunkcie b)
następującego zadania:
Zadanie (11). Prostokąt
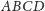 jest zawarty w kwadracie o boku
długości
jest zawarty w kwadracie o boku
długości
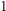 i żaden z punktów
i żaden z punktów
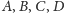 nie leży na brzegu
tego kwadratu. Wynika z tego, że
nie leży na brzegu
tego kwadratu. Wynika z tego, że
- a)
-
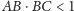 ;
;
- b)
-
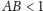 ;
;
- c)
-
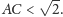
Z kolei w następującym zadaniu najmniej uczestników, bo niespełna
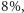 otrzymało
otrzymało
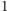 punkt. W zadaniu tym także najwięcej uczniów
(ponad
punkt. W zadaniu tym także najwięcej uczniów
(ponad
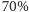 ) uzyskało
) uzyskało
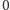 punktów.
punktów.
Zadanie (14). Liczba
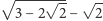 jest
jest
- a)
- całkowita;
- b)
- niewymierna;
- c)
- dodatnia.
Podczas gdy większość uczestników starała się uzyskać jak najwięcej
punktów, nie brakowało też takich, którzy chcieli zdobyć ich jak
najmniej. Jeden uczeń, który nie znosi zadań zamkniętych, chwalił się na
Facebook’owym profilu OMG, że w ramach protestu odpowiadał na wszystkie
pytania odwrotnie: tam, gdzie miało być „Tak” pisał „Nie” i na odwrót. Miało
mu to zapewnić uzyskanie 0 punktów, przy jednoczesnym udzieleniu
odpowiedzi na wszystkie pytania. Jednak nie do końca mu się ta sztuka udała.
Przez nieuwagę dostał 1 punkt (dwa razy po
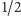 punktu). Sześciu innych
zawodników było lepszych od niego w tej rywalizacji: pięciu otrzymało
punktu). Sześciu innych
zawodników było lepszych od niego w tej rywalizacji: pięciu otrzymało
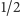 punktu, a tylko jednej osobie udało się uzyskać 0 punktów, podając
odpowiedzi do wszystkich pytań!
punktu, a tylko jednej osobie udało się uzyskać 0 punktów, podając
odpowiedzi do wszystkich pytań!
Na szczególne wyróżnienie zasługują jednak osoby, które uzyskały
maksymalną liczbę punktów. Na ponad 14000 było ich zaledwie 10. Są to:
Dominika BAKALARZ, Anna CZERWIŃSKA, Ewa ZIELIŃSKA,
Tomasz KLEINER, Michał MADEJA, Jan MIRKIEWICZ, Konrad MAJEWSKI,
Cyprian MATACZYŃSKI, Piotr PAWLAK i Patryk SZCZEPAŃSKI.