Interpolacja fraktalna, czyli dwukrotne fałszerstwo na zamówienie
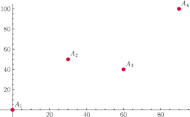
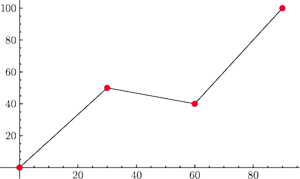
Rys. 1
Urządzenie pomiarowe zmierzyło wartości pewnej wielkości w czterech momentach (Rys. 1). Wiemy więc bardzo niewiele o zależności tej wielkości od czasu.
Mimo to chcielibyśmy odtworzyć brakujące punkty wykresu, kierując się następującymi informacjami:
- pomiędzy każdymi dwoma kolejnymi punktami dzieje się tak dużo, jak pomiędzy pierwszym i ostatnim, tzn. kawałki wykresów pomiędzy kolejnymi punktami są takie, jak cały wykres po odpowiednim „przeskalowaniu”,
- wykres funkcji jest linią ciągłą.
Z wielu możliwych funkcji, które spełniają powyższe warunki, wybierzemy taką, która da się łatwo opisać. Punkty z wykresu tej funkcji potraktujemy jako uzupełnienie brakujących danych. Będzie to więc świadome fałszerstwo.
Konstrukcja interpolacji fraktalnej
- Tworzymy łamaną łączącą kolejne punkty
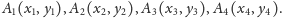 Otrzymujemy
w ten sposób interpolację kawałkami liniową
Otrzymujemy
w ten sposób interpolację kawałkami liniową
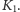
- Otrzymaną łamaną
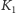 przeskalujemy (zwęzimy i ściśniemy) i wstawimy
pomiędzy punkty
przeskalujemy (zwęzimy i ściśniemy) i wstawimy
pomiędzy punkty
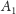 i
i
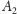 (Rys. 3). Podobnie łamaną
(Rys. 3). Podobnie łamaną
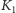 przekształcimy i wstawimy kolejno pomiędzy punkty
przekształcimy i wstawimy kolejno pomiędzy punkty
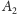 i
i
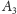 oraz
oraz
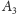 i
i
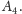
- W każdym następnym kroku powtarzamy te same czynności:
krzywą otrzymaną w kroku poprzednim odwzorowujemy
przekształceniem
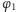 pomiędzy punkty
pomiędzy punkty
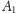 i
i
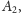 przekształceniem
przekształceniem
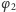 pomiędzy punkty
pomiędzy punkty
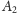 i
i
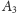 oraz przekształceniem
oraz przekształceniem
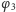 pomiędzy
punkty
pomiędzy
punkty
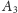 i
i
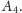
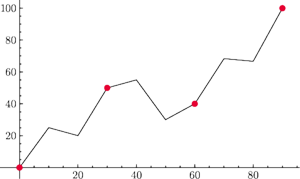
Im więcej tych kroków wykonamy, tym dokładniejsze przybliżenie granicznej
krzywej fraktalnej dostaniemy. W granicznej krzywej
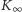 każdy kawałek
pomiędzy punktami
każdy kawałek
pomiędzy punktami
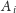 oraz
oraz
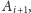 dla
dla
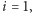 2 lub 3, jest
podobny (afinicznie) do całości, a cała krzywa jest sumą swoich trzech kopii:
2 lub 3, jest
podobny (afinicznie) do całości, a cała krzywa jest sumą swoich trzech kopii:
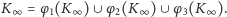
Cały artykuł dostępny jest w formacie pdf.
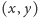 przejdzie na punkt
o współrzędnych
przejdzie na punkt
o współrzędnych
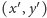 zgodnie z regułą
zgodnie z regułą

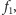 które odwzorowuje łamaną
które odwzorowuje łamaną
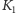 w łamaną
łączącą punkty
w łamaną
łączącą punkty
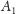 i
i
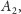 mamy
mamy
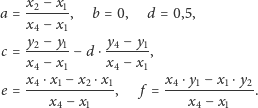
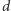 możemy wybrać dowolnie spomiędzy liczb
z przedziału
możemy wybrać dowolnie spomiędzy liczb
z przedziału
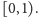 Od niego zależy, jak bardzo „postrzępiona” jest
końcowa krzywa fraktalna.
Od niego zależy, jak bardzo „postrzępiona” jest
końcowa krzywa fraktalna.
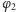 i
i
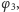 które
„wstawiają” łamaną
które
„wstawiają” łamaną
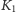 odpowiednio pomiędzy punkty
odpowiednio pomiędzy punkty
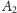 i
i
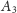 oraz
oraz
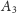 i
i