Problem więźniów - o pewnych własnościach losowych permutacji
W pewnym zakładzie karnym przebywa stu skazanych, ponumerowanych liczbami od 1 do 100: 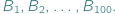 Strażnik zaproponował im następującą grę: sto kartek z ich numerami umieszcza w stu skrytkach, po jednej kartce w każdej skrytce. Sposób rozmieszczenia kartek nie jest znany więźniom. Następnie strażnik pozwala każdemu z więźniów sprawdzić dokładnie połowę skrytek. Sprawdzający wchodzi do pokoju ze skrytkami sam, a po swojej turze musi zostawić pokój w stanie nienaruszonym i jedynie poinformować nadzorcę, czy odnalazł swój numer, czy też nie. Nie komunikuje się później z pozostałymi więźniami. Osadzeni wygrywają wyjście na wolność wtedy i tylko wtedy, gdy każdy z nich zdoła odnaleźć swój numer. Jaka jest szansa na to, że im się to uda?
Strażnik zaproponował im następującą grę: sto kartek z ich numerami umieszcza w stu skrytkach, po jednej kartce w każdej skrytce. Sposób rozmieszczenia kartek nie jest znany więźniom. Następnie strażnik pozwala każdemu z więźniów sprawdzić dokładnie połowę skrytek. Sprawdzający wchodzi do pokoju ze skrytkami sam, a po swojej turze musi zostawić pokój w stanie nienaruszonym i jedynie poinformować nadzorcę, czy odnalazł swój numer, czy też nie. Nie komunikuje się później z pozostałymi więźniami. Osadzeni wygrywają wyjście na wolność wtedy i tylko wtedy, gdy każdy z nich zdoła odnaleźć swój numer. Jaka jest szansa na to, że im się to uda?
Na pierwszy rzut oka więźniowie są w dramatycznej sytuacji. Każdy z nich ma szansę 50% na odnalezienie numeru w swojej turze, więc wydawać by się mogło, że szansa na sukces wszystkich wynosi 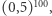 czyli przeraźliwie mało. Okazuje się, że ta intuicja jest błędna. Opowiem o strategii pozwalającej na zmaksymalizowanie prawdopodobieństwa wygranej w opisanej grze - dzięki niej szansa więźniów na uzyskanie wolności wynosi... ponad 30%!
czyli przeraźliwie mało. Okazuje się, że ta intuicja jest błędna. Opowiem o strategii pozwalającej na zmaksymalizowanie prawdopodobieństwa wygranej w opisanej grze - dzięki niej szansa więźniów na uzyskanie wolności wynosi... ponad 30%!
Wspomniana strategia jest następująca:
więzień 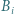 swoją turę rozpoczyna od sprawdzenia
swoją turę rozpoczyna od sprawdzenia 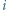 -tej szafki. Jeśli nie znajdzie tam swojego numeru, tj. znajdzie numer
-tej szafki. Jeśli nie znajdzie tam swojego numeru, tj. znajdzie numer 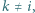 to sprawdza
to sprawdza 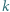 -tą szafkę. Postępuje w ten sposób aż do momentu sukcesu lub wyczerpania się puli szafek możliwych do sprawdzenia.
-tą szafkę. Postępuje w ten sposób aż do momentu sukcesu lub wyczerpania się puli szafek możliwych do sprawdzenia.
Dla przykładu, ograniczmy się do przypadku 10 więźniów, żeby z łatwością prześledzić przebieg rozgrywki. Załóżmy, że w szafkach znajdują się kolejno numery: 3, 2, 8, 5, 9, 4, 6, 10, 7, 1. Rozgrywka więźnia 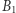 krok po kroku przedstawia się następująco:
krok po kroku przedstawia się następująco:
Sprawdza szafkę 1.
Znajduje w niej 3
Sprawdza szafkę 3.
Znajduje w niej 8
Sprawdza szafkę 8.
Znajduje w niej 10
Sprawdza szafkę 10.
Znajduje w niej 1
Zwycięsko kończy swoją turę.
Zauważmy, że w momencie znalezienia swojego numeru (czyli po czterech sprawdzeniach) więzień 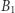 już wie, że więźniowie
już wie, że więźniowie 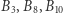 będą sprawdzać dokładnie te same szafki co on, w pewnym cyklicznym przesunięciu, i każdy z nich odniesie sukces w czwartym kroku. Sukcesy więźniów nie są zatem, przy zastosowaniu tej strategii, zdarzeniami niezależnymi, a więc - chociaż wciąż każdy z nich ma szansę 50% na znalezienie swojego numerka - szansa na sukces wszystkich więźniów nie musi być tak mała, jak podpowiadała opisana na wstępie intuicja. A ile ta szansa wynosi dokładnie? Aby odpowiedzieć na to pytanie, musimy odrobinę sformalizować naszą grę.
będą sprawdzać dokładnie te same szafki co on, w pewnym cyklicznym przesunięciu, i każdy z nich odniesie sukces w czwartym kroku. Sukcesy więźniów nie są zatem, przy zastosowaniu tej strategii, zdarzeniami niezależnymi, a więc - chociaż wciąż każdy z nich ma szansę 50% na znalezienie swojego numerka - szansa na sukces wszystkich więźniów nie musi być tak mała, jak podpowiadała opisana na wstępie intuicja. A ile ta szansa wynosi dokładnie? Aby odpowiedzieć na to pytanie, musimy odrobinę sformalizować naszą grę.
Gdy spojrzymy na tę zagadkę jak na problem matematyczny, rozmieszczanie przez strażnika numerów więźniów w szafkach ponumerowanych od 1 do 100 odpowiada losowaniu przez niego pewnej permutacji 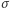 zbioru
zbioru 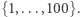 Zgodnie z opisaną strategią
Zgodnie z opisaną strategią 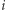 -ty więzień rozpocznie od sprawdzenia
-ty więzień rozpocznie od sprawdzenia 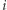 -tej szafki, w której znajdzie numerek
-tej szafki, w której znajdzie numerek 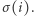 Jeśli
Jeśli 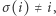 to więzień kontynuuje i otwiera szafkę o numerze
to więzień kontynuuje i otwiera szafkę o numerze 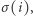 w której znajduje
w której znajduje 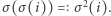 O ile wcześniej nie znalazł swojego numerka, w
O ile wcześniej nie znalazł swojego numerka, w 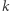 -tym podejściu otworzy szafkę
-tym podejściu otworzy szafkę 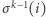 i znajdzie tam numer
i znajdzie tam numer 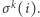 W tej sytuacji
W tej sytuacji 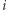 -ty więzień odnajdzie swój numer, jeśli liczba
-ty więzień odnajdzie swój numer, jeśli liczba 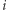 jest elementem cyklu długości nie większej niż 50. Zatem sukces więźniów jest równoważny temu, że w permutacji
jest elementem cyklu długości nie większej niż 50. Zatem sukces więźniów jest równoważny temu, że w permutacji 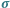 nie ma cyklu długości większej niż 50. Szansa na ich porażkę to zatem szansa na wystąpienie takiego cyklu w losowej permutacji liczb
nie ma cyklu długości większej niż 50. Szansa na ich porażkę to zatem szansa na wystąpienie takiego cyklu w losowej permutacji liczb 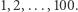
Obliczanie prawdopodobieństwa przegranej przy opisanej strategii sprowadza się więc do znalezienia liczby permutacji zbioru 100-elementowego, które mają cykl długości 51 lub dłuższy. W ogólności sprawę wyjaśnia następujące twierdzenie.
Dowód. Zwróćmy uwagę, że permutacja może mieć co najwyżej jeden cykl długości większej niż 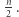 Wybieramy na
Wybieramy na 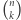 sposobów, które
sposobów, które 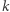 elementy mają wejść w skład cyklu
elementy mają wejść w skład cyklu 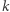 -elementowego. Ustawiamy je na
-elementowego. Ustawiamy je na 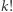 sposobów. Cykl nie zmienia się przy przesunięciach - możliwych przesunięć w prawo reprezentacji cyklu jako
sposobów. Cykl nie zmienia się przy przesunięciach - możliwych przesunięć w prawo reprezentacji cyklu jako 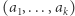 jest dokładnie
jest dokładnie 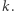 Liczba możliwych istotnie różnych ustawień wybranych
Liczba możliwych istotnie różnych ustawień wybranych 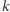 elementów to zatem
elementów to zatem 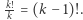 Pozostałe
Pozostałe 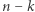 elementy permutujemy na
elementy permutujemy na 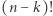 sposobów. Liczba permutacji zbioru
sposobów. Liczba permutacji zbioru 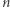 -elementowego, które w swoim rozkładzie zawierają cykl długości
-elementowego, które w swoim rozkładzie zawierają cykl długości 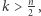 to w takim razie:
to w takim razie: 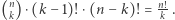
Zgodnie z powyższym twierdzeniem dla 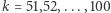 cykle długości
cykle długości 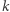 stanowią
stanowią 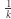 wszystkich permutacji. Prawdopodobieństwo otrzymania permutacji posiadającej cykl długości 51 lub dłuższy jest wobec tego równe:
wszystkich permutacji. Prawdopodobieństwo otrzymania permutacji posiadającej cykl długości 51 lub dłuższy jest wobec tego równe:
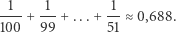 |
Szansa więźniów na wygraną wynosi więc w przybliżeniu 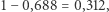 czyli w ponad 30% przypadków więźniowie wyjdą na wolność.
czyli w ponad 30% przypadków więźniowie wyjdą na wolność.
Pozostaje uzasadnić, dlaczego jest to najlepsza możliwa strategia. Nie jest zaskakujące, że dowód optymalności będzie bardziej skomplikowany, jest jednak wielce pouczający! Dla uproszczenia będziemy znów rozważać przypadek z dziesięcioma więźniami, 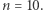 Rozważmy subtelną zmianę reguł gry: tym razem każdy z więźniów musi otwierać szafki do momentu, w którym znajdzie swój numer. Nie ma ograniczeń co do liczby sprawdzeń, jednak więźniowie przegrywają, gdy na końcu okaże się, że któryś z nich otworzył ponad połowę szafek. Taka zmiana nie wpływa na prawdopodobieństwo zwycięstwa w rozważanej przez nas grze, którą dalej będziemy nazywać grą A.
Rozważmy subtelną zmianę reguł gry: tym razem każdy z więźniów musi otwierać szafki do momentu, w którym znajdzie swój numer. Nie ma ograniczeń co do liczby sprawdzeń, jednak więźniowie przegrywają, gdy na końcu okaże się, że któryś z nich otworzył ponad połowę szafek. Taka zmiana nie wpływa na prawdopodobieństwo zwycięstwa w rozważanej przez nas grze, którą dalej będziemy nazywać grą A.
Opiszemy teraz zasady nieco innej gry, nazywanej przez nas dalej grą B. Tym razem strażnik zaprasza wszystkich więźniów jednocześnie do pokoju z szafkami, tak że mogą oni obserwować przebieg rozgrywki. Załóżmy, że rozmieścił on numery w kolejności: 2, 5, 10, 3, 9, 4, 6, 8, 1, 7. Więzień 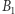 rozpoczyna sprawdzanie. Szuka do momentu, w którym znajdzie swój numer, przy czym nie zamyka już otwartych szafek. Inni gracze widzą, jakie numery zostały już znalezione. Ponadto jeśli
rozpoczyna sprawdzanie. Szuka do momentu, w którym znajdzie swój numer, przy czym nie zamyka już otwartych szafek. Inni gracze widzą, jakie numery zostały już znalezione. Ponadto jeśli 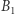 odnajdzie (postępując według jakiejś swojej strategii) kolejno numery 4, 7, 2, 1, to
odnajdzie (postępując według jakiejś swojej strategii) kolejno numery 4, 7, 2, 1, to 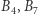 i
i 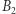 już nie startują w grze, ich numery zostały odnalezione. Kolejnym sprawdzającym będzie teraz więzień o najmniejszym numerze, który nie został znaleziony w poprzedniej turze, czyli
już nie startują w grze, ich numery zostały odnalezione. Kolejnym sprawdzającym będzie teraz więzień o najmniejszym numerze, który nie został znaleziony w poprzedniej turze, czyli 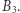 Odnajduje on numery 9, 5, 10, 6, 3. Pozostały gracz
Odnajduje on numery 9, 5, 10, 6, 3. Pozostały gracz 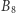 w jednym kroku odnajduje swój numer. Na końcu sprawdzamy, czy któryś z graczy otworzył więcej niż 5 szafek. Tym razem więźniom udało się wygrać.
w jednym kroku odnajduje swój numer. Na końcu sprawdzamy, czy któryś z graczy otworzył więcej niż 5 szafek. Tym razem więźniom udało się wygrać.
Jest jasne, że gra 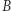 jest dla więźniów korzystniejsza niż gra
jest dla więźniów korzystniejsza niż gra 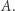 Oznacza to w szczególności, że najlepsza możliwa strategia w grze
Oznacza to w szczególności, że najlepsza możliwa strategia w grze 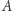 daje nie większą szansę na sukces niż najlepsza możliwa strategia w grze
daje nie większą szansę na sukces niż najlepsza możliwa strategia w grze 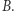 Pokażemy, że każda strategia w grze
Pokażemy, że każda strategia w grze 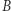 daje prawdopodobieństwo sukcesu takie, jak opisana wcześniej strategia dla gry
daje prawdopodobieństwo sukcesu takie, jak opisana wcześniej strategia dla gry 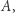 co będzie dowodzić optymalności tej ostatniej.
co będzie dowodzić optymalności tej ostatniej.
Powróćmy do rozważanego wcześniej przykładu rozgrywki w grę 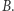 Powiedzmy, że każdy z wykonujących ruchy graczy zapisywał numery kolejno otwieranych szafek w jednym ciągu. Tutaj dałoby to ciąg
Powiedzmy, że każdy z wykonujących ruchy graczy zapisywał numery kolejno otwieranych szafek w jednym ciągu. Tutaj dałoby to ciąg 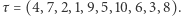 Uzyskany ciąg jest pewną permutacją zbioru liczb od 1 do 10, potencjalnie dowolną. Ponadto można z niego wywnioskować "bloki" numerów odkrywanych przez kolejnych graczy: każdy blok ma kończyć się najmniejszym "jeszcze niezblokowanym" numerem (4,7,2,1 wraz z 9,5,10,6,3 oraz 8 to trzy bloki). Więźniowie wygrywają grę
Uzyskany ciąg jest pewną permutacją zbioru liczb od 1 do 10, potencjalnie dowolną. Ponadto można z niego wywnioskować "bloki" numerów odkrywanych przez kolejnych graczy: każdy blok ma kończyć się najmniejszym "jeszcze niezblokowanym" numerem (4,7,2,1 wraz z 9,5,10,6,3 oraz 8 to trzy bloki). Więźniowie wygrywają grę 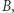 jeśli uzyskana permutacja
jeśli uzyskana permutacja 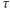 nie ma bloku długości większej niż 5.
nie ma bloku długości większej niż 5.
Kluczowym spostrzeżeniem jest teraz to, że jeśli każda z permutacji 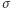 rozmieszczenia kartek w szafkach była wylosowana z tym samym prawdopodobieństwem, to w wyniku każda z permutacji
rozmieszczenia kartek w szafkach była wylosowana z tym samym prawdopodobieństwem, to w wyniku każda z permutacji 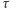 również będzie uzyskana z tym samym prawdopodobieństwem. Dokładne wyjaśnienie tego faktu nie jest długie, jednak mało interesujące i mogłoby się zdawać "przeformalizowane", zamiast tego przedstawimy zatem przekonującą intuicję.
również będzie uzyskana z tym samym prawdopodobieństwem. Dokładne wyjaśnienie tego faktu nie jest długie, jednak mało interesujące i mogłoby się zdawać "przeformalizowane", zamiast tego przedstawimy zatem przekonującą intuicję.
Prawdopodobieństwo pojawienia się danego uporządkowania numerków w szafkach wynosi 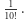 Niezależnie od tego, którą szafkę postanowi jako pierwszą sprawdzić
Niezależnie od tego, którą szafkę postanowi jako pierwszą sprawdzić 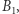 prawdopodobieństwo wystąpienia w niej na przykład 9 wynosi
prawdopodobieństwo wystąpienia w niej na przykład 9 wynosi 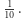 Pod warunkiem, że owa dziewiątka zostanie odszukana jako pierwsza, prawdopodobieństwo odszukania na przykład 1 w drugim kroku jest równe
Pod warunkiem, że owa dziewiątka zostanie odszukana jako pierwsza, prawdopodobieństwo odszukania na przykład 1 w drugim kroku jest równe 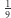 (ze względu na "symetrię" wyjściowego losowania
(ze względu na "symetrię" wyjściowego losowania 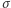 ). W tym wypadku nie ma żadnego znaczenia, jaką strategią posłużą się więźniowie, gdyż z punktu widzenia ich decyzji każdy z nieodkrytych jeszcze numerków pełni tę samą rolę. Powtarzając to rozumowanie, dochodzimy do wniosku, że każda wynikowa permutacja
). W tym wypadku nie ma żadnego znaczenia, jaką strategią posłużą się więźniowie, gdyż z punktu widzenia ich decyzji każdy z nieodkrytych jeszcze numerków pełni tę samą rolę. Powtarzając to rozumowanie, dochodzimy do wniosku, że każda wynikowa permutacja  może zostać uzyskana z tym samym prawdopodobieństwem
może zostać uzyskana z tym samym prawdopodobieństwem 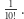
Prawdopodobieństwo przegranej jest zatem dla każdej strategii takie samo - jest to prawdopodobieństwo, że losowo wybrana permutacja ma blok dłuższy niż 5. W ilu przypadkach z 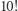 możliwych więźniowie przegrają? Otóż dokładnie w ten sam sposób, jak udowodniliśmy twierdzenie, możemy pokazać, że permutacji, które mają blok długości
możliwych więźniowie przegrają? Otóż dokładnie w ten sam sposób, jak udowodniliśmy twierdzenie, możemy pokazać, że permutacji, które mają blok długości 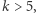 jest dokładnie
jest dokładnie 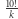 - szczegóły na marginesie.
- szczegóły na marginesie.
W tej sytuacji więźniowie wygrywają grę B z prawdopodobieństwem równym
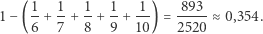 |
Prawdopodobieństwo zwycięstwa w grze B jest równe prawdopodobieństwu sukcesu w grze A, w której wykorzystano strategię poruszania się po cyklach.
Więźniowie mogą zaadaptować dowolną strategię z gry A do gry B. Przy ustalonym ustawieniu numerów w szafkach, jeśli dana strategia poprowadziła do zwycięskiej kolejności otwierania w grze A, to ta kolejność będzie również zwycięska w grze B. W takim razie, gdyby istniała lepsza strategia dla gry A, niż przechodzenie przez cykle, to po zaadaptowaniu do gry B musiałaby również dawać w niej większe szanse na zwycięstwo. Jednakże nie jest to możliwe, ponieważ wszystkie strategie w grze B prowadzą do takich szans na zwycięstwo, jak przechodzenie przez cykle. Jest to zatem strategia optymalna.
Udało nam się rozwikłać problem więźniów - wskazaliśmy najlepszą możliwą strategię. Zagadnienie to ma jednak tę własność, że generuje dużą liczbę pytań, które można sobie zadać, kiedy już pozna się jego rozwiązanie. Co się stanie, gdy szafek będzie dwukrotnie więcej niż więźniów i połowa z nich będzie pusta? Wtedy oczywiście strategia przechodzenia przez cykle nie działa, bo można natrafić na pustą szafkę. Czy w takim wariancie można stwierdzić, że razem ze zwiększającą się liczbą graczy, prawdopodobieństwo ich wygranej będzie zmniejszać się aż do 0? Okazuje się, że wciąż jest to problem otwarty. Można również zadać pytanie, co się stanie, jeśli strażnik więzienia byłby niezwykle dociekliwym Czytelnikiem Delty i przewidział, że więźniowie będą postępować zgodnie ze strategią przechodzenia przez cykle. Wtedy mógłby ustawić numery specjalnie w taki sposób, by pojawił się cykl o długości większej niż połowa liczby szafek. Zagadką dla Czytelnika równie dociekliwego, co ów strażnik, pozostaje znalezienie sposobu, w jaki więźniowie mogliby poradzić sobie wówczas z pilnującym ich matematykiem.
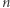
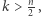
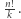
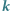 w permutacji
w permutacji 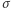 nazwiemy ciąg elementów
nazwiemy ciąg elementów 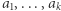 takich, że
takich, że 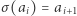 dla
dla 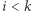 oraz
oraz 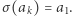
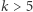 mamy
mamy 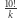 permutacji z blokiem długości
permutacji z blokiem długości 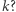 Taki blok może być co najwyżej jeden. Najpierw na
Taki blok może być co najwyżej jeden. Najpierw na 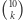 sposobów wybieramy
sposobów wybieramy 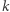 elementów, które mają być częścią bloku. Najmniejszy z nich
elementów, które mają być częścią bloku. Najmniejszy z nich 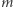 musi znaleźć się na końcu, a pozostałe możemy ustawić na
musi znaleźć się na końcu, a pozostałe możemy ustawić na 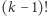 sposobów. Elementy spoza bloku możemy ustawić na
sposobów. Elementy spoza bloku możemy ustawić na 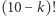 sposobów i dla każdego z nich w dokładnie jednym miejscu możemy ustawić wyróżniony blok, tzn. tuż po tym, jak pojawią się wszystkie elementy od 1 do
sposobów i dla każdego z nich w dokładnie jednym miejscu możemy ustawić wyróżniony blok, tzn. tuż po tym, jak pojawią się wszystkie elementy od 1 do