Lemat Spernera, czyli co wspólnego mają trójkąty i sprawiedliwy podział
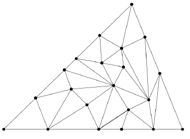
Rys. 1. Triangulacja trójkąta
Poprzez triangulację będziemy rozumieć podział figury na trójkąty (Rys. 1). W dalszej części artykułu będziemy zajmować się kolorowaniem wierzchołków triangulacji pewnego trójkąta...
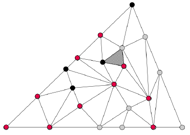
Rys. 2
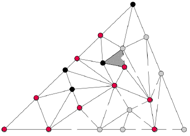
Rys. 3
Wyjściowy trójkąt będziemy nazywali dużym, natomiast "jednostkowe" trójkąty triangulacji będziemy nazywać małymi. Kluczowym elementem tych rozważań będzie następujący lemat:
Lemat 1 (Sperner). Weźmy dowolną triangulację trójkąta i pokolorujmy każdy wierzchołek na czarno, szaro lub czerwono, zachowując dwa warunki:
- duży trójkąt jest różnokolorowy (to znaczy, że jego wierzchołki są pokolorowane parami różnymi kolorami),
- na żadnym boku dużego trójkąta nie mogą występować wszystkie trzy kolory.
Wtedy istnieje różnokolorowy mały trójkąt (Rys. 2).
Dowód. Załóżmy, że nie ma takiego małego trójkąta. Poprzez drzwi będziemy rozumieli każdą krawędź między czerwonym a szarym wierzchołkiem (na rysunku 3 oznaczone przerwanym odcinkiem). W dalszej części dowodu będziemy myśleli o małych trójkątach jako o pokojach, między którymi będziemy chodzić. Zauważmy, że wszystkie drzwi na bokach dużego trójkąta mogą być tylko na jednym boku (powiedzmy, że jest to "dolny" bok, tak jak na Rys. 3). Co więcej, na tym boku jest ich nieparzyście wiele.
Sprawdźmy, ile drzwi może znajdować się w pokojach. Łatwo zauważyć, że żaden pokój nie może mieć dokładnie trojga. Jedne drzwi mógłby mieć tylko w wypadku, gdyby był różnokolorowy (a założyliśmy, że takiego nie ma). Wszystkie pokoje mają zatem albo 0 albo 2 drzwi.
Możemy teraz zacząć chodzić po pokojach. Każdych drzwi będziemy używać co najwyżej raz. Najpierw "wejdziemy" do dużego trójkąta przez któreś z drzwi na jego dolnym boku i będziemy chodzić do momentu, gdy "wyjdziemy" z dużego trójkąta przez jakieś drzwi na jego dolnym boku. Fakt, że każdy pokój ma albo 0, albo 2 drzwi, gwarantuje nam, że z każdego pokoju, do którego wejdziemy, możemy też wyjść, a ponadto nigdy dwukrotnie nie wejdziemy do tego samego pokoju. Całą procedurę powtarzamy, aż wyczerpiemy drzwi na dolnym boku dużego trójkąta. Z drugiej strony oznacza to, że drzwi na tym boku jest parzyście wiele, i otrzymujemy sprzeczność.
Zauważmy, że jest to tak naprawdę dowód konstrukcyjny i przedstawia on algorytm na znalezienie takiego trójkąta. Chcąc znaleźć różnokolorowy pokój, chodzimy do momentu, aż utkniemy. Zwróćmy również uwagę, że z powyższego dowodu wynika, iż różnokolorowych małych trójkątów jest nieparzyście wiele. Wynika stąd, że lemat Spernera działa dla większej liczby wymiarów i kolorów. Dowód przebiega w podobny sposób przy użyciu indukcji. Fakt, że liczba drzwi na dolnej ścianie sympleksu (czyli wielowymiarowego trójkąta) jest nieparzysta, to w rzeczywistości "poprzednio-wymiarowa" wersja lematu Spernera.

Rys. 4
Problem 1. Aldona, Bogumił i Celina chcą podzielić między siebie ciasto. Jak to zrobić, żeby nikt nikomu nie zazdrościł? Każdy może mieć różne preferencje co do tego, która część ciasta jest najlepsza.
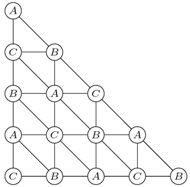
Rys. 5
Rozwiązanie. Ustalmy dowolnie pewien kierunek i załóżmy, że w tym kierunku ciasto ma szerokość 1. Będziemy ciąć prostokątne ciasto prostopadle do tego kierunku. Możemy wtedy przedstawić każde takie cięcie jako parę 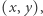 gdzie
gdzie 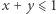 i kawałki będą mieć odpowiednio szerokości
i kawałki będą mieć odpowiednio szerokości 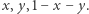 Kawałki nazwiemy odpowiednio czarny, szary i czerwony (Rys. 4).
Kawałki nazwiemy odpowiednio czarny, szary i czerwony (Rys. 4).
Zbiór wszystkich takich par 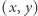 tworzy trójkąt o wierzchołkach
tworzy trójkąt o wierzchołkach 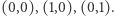 Potnijmy go na bardzo dużo mniejszych trójkątów. Oznaczmy wierzchołki literami
Potnijmy go na bardzo dużo mniejszych trójkątów. Oznaczmy wierzchołki literami 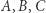 tak, że w każdym małym trójkącie wśród oznaczeń wierzchołków będą wszystkie litery (tak jak na Rys. 5).
tak, że w każdym małym trójkącie wśród oznaczeń wierzchołków będą wszystkie litery (tak jak na Rys. 5).
Następnie dla każdego wierzchołka 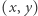 pytamy odpowiadającą mu osobę (
pytamy odpowiadającą mu osobę ( 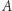 ldonę,
ldonę, 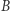 ogumiła lub
ogumiła lub 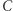 elinę), który kawałek by wybrał, gdyby właśnie taki podział ciasta miał miejsce. W ten sposób kolorujemy wierzchołki na czarno, szaro lub czerwono. Łatwo sprawdzić, że ten podział wierzchołków spełnia warunki lematu Spernera. W końcu na krawędziach dużego trójkąta któryś kawałek jest pusty, a nikt nie wybierze pustego kawałka! W szczególności w wierzchołkach dużego trójkąta niepusty będzie tylko jeden kawałek, w każdym inny. Zatem istnieje różnokolorowy mały trójkąt. Oznacza to, że istnieją trzy bardzo podobne podziały ciasta, w których każdy woli inny kawałek. Możemy więc wziąć np. średnią z nich (środek ciężkości małego trójkąta) i podzielić kawałki zgodnie z preferencjami. Mogliśmy wziąć dowolnie drobną triangulację, więc różnice między kawałkami będą minimalne.
elinę), który kawałek by wybrał, gdyby właśnie taki podział ciasta miał miejsce. W ten sposób kolorujemy wierzchołki na czarno, szaro lub czerwono. Łatwo sprawdzić, że ten podział wierzchołków spełnia warunki lematu Spernera. W końcu na krawędziach dużego trójkąta któryś kawałek jest pusty, a nikt nie wybierze pustego kawałka! W szczególności w wierzchołkach dużego trójkąta niepusty będzie tylko jeden kawałek, w każdym inny. Zatem istnieje różnokolorowy mały trójkąt. Oznacza to, że istnieją trzy bardzo podobne podziały ciasta, w których każdy woli inny kawałek. Możemy więc wziąć np. średnią z nich (środek ciężkości małego trójkąta) i podzielić kawałki zgodnie z preferencjami. Mogliśmy wziąć dowolnie drobną triangulację, więc różnice między kawałkami będą minimalne.
Problem 2. Aldona, Bogumił i Celina chcą razem wynająć trzypokojowe mieszkanie. Czynsz za całe mieszkanie wynosi 3000 złotych. Jak podzielić między nich pokoje i czynsz tak, żeby nikt nikomu nie zazdrościł?
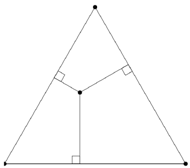
Rys. 6
Rozwiązanie. Skorzystamy ze znanej własności trójkąta równobocznego, takiej że dla każdego punktu wewnątrz tego trójkąta suma 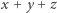 jest stała (Rys. 6). Weźmy zatem "regularną" triangulację (Rys. 6) i powiedzmy, że dla każdego punktu
jest stała (Rys. 6). Weźmy zatem "regularną" triangulację (Rys. 6) i powiedzmy, że dla każdego punktu 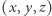 zachodzi
zachodzi 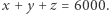 Dalej postępujemy analogicznie do poprzedniego zadania: oznaczmy wierzchołki literami
Dalej postępujemy analogicznie do poprzedniego zadania: oznaczmy wierzchołki literami 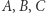 podobnie jak na rysunku 5, tylko że dla trójkąta równobocznego. Następnie dla każdego wierzchołka
podobnie jak na rysunku 5, tylko że dla trójkąta równobocznego. Następnie dla każdego wierzchołka 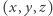 pytamy odpowiadającą mu osobę, który pokój by wybrała, gdyby ceny czarnego, szarego i czerwonego pokoju wynosiły odpowiednio
pytamy odpowiadającą mu osobę, który pokój by wybrała, gdyby ceny czarnego, szarego i czerwonego pokoju wynosiły odpowiednio 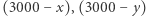 i
i 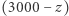 złotych (dopuszczamy "ujemne ceny", tzn. dopłacanie lokatorowi za mieszkanie w danym pokoju). Zauważmy, że istotnie te ceny sumują się do całego czynszu, czyli 3000 złotych. W ten sposób kolorujemy wszystkie wierzchołki. Zakładamy przy tym, że nikt nie weźmie pokoju za 3000 złotych (nikt nie chce płacić sam czynszu za całe mieszkanie). Łatwo sprawdzić, że wtedy to kolorowanie spełnia warunki lematu Spernera. Istnieje zatem mały różnokolorowy trójkąt, a więc trzy bardzo podobne podziały czynszu, w których każdy woli inny pokój. Podobnie jak w poprzednim zadaniu, możemy wziąć np. średnią z tych trzech podziałów czynszu i rozdzielić pokoje zgodnie z preferencjami. Mogliśmy wziąć dowolnie drobną triangulację (podzielić na dowolnie dużo małych trójkątów), więc różnice w zadowoleniu lokatorów będą minimalne.
złotych (dopuszczamy "ujemne ceny", tzn. dopłacanie lokatorowi za mieszkanie w danym pokoju). Zauważmy, że istotnie te ceny sumują się do całego czynszu, czyli 3000 złotych. W ten sposób kolorujemy wszystkie wierzchołki. Zakładamy przy tym, że nikt nie weźmie pokoju za 3000 złotych (nikt nie chce płacić sam czynszu za całe mieszkanie). Łatwo sprawdzić, że wtedy to kolorowanie spełnia warunki lematu Spernera. Istnieje zatem mały różnokolorowy trójkąt, a więc trzy bardzo podobne podziały czynszu, w których każdy woli inny pokój. Podobnie jak w poprzednim zadaniu, możemy wziąć np. średnią z tych trzech podziałów czynszu i rozdzielić pokoje zgodnie z preferencjami. Mogliśmy wziąć dowolnie drobną triangulację (podzielić na dowolnie dużo małych trójkątów), więc różnice w zadowoleniu lokatorów będą minimalne.
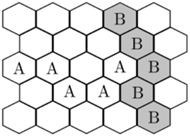
Rys. 7
Problem 3. Aldona i Bogumił grają w Hex. Jest to gra polegająca na naprzemiennym oznaczaniu sześciokątnych pól na "kwadratowej" (tyle samo sześciokątów w pionie i w poziomie) planszy. Celem Aldony jest utworzenie ścieżki od lewej do prawej krawędzi, a celem Bogumiła - od górnej do dolnej (np. na Rys. 7 wygrywa Bogumił). Aldona zaczyna. Czy może zapewnić sobie zwycięstwo?
Rozwiązanie. Udowodnimy, że istnieje strategia wygrywająca dla Aldony. Najpierw zauważmy, że na mocy twierdzenia Zermelo zachodzi dokładnie jedno z poniższych:
- (1)
- Aldona ma strategię wygrywającą.
- (2)
- Bogumił ma strategię wygrywającą.
- (3)
- Oboje mają strategię remisującą.
Udowodnimy, że niemożliwy jest przypadek 2. Załóżmy, że Bogumił miałby strategię wygrywającą. Wtedy Aldona mogłaby zacząć grę, oznaczając dowolne pole (co nie może jej w żaden sposób zaszkodzić) i następnie podążać za strategią Bogumiła. Wygrałaby wtedy Aldona, i otrzymujemy sprzeczność (ten pomysł nazywa się "złodziejem strategii", możecie o tym poczytać więcej w Delcie 5/2017).

Rys. 8
Wystarczy zatem udowodnić, że niemożliwy jest remis. Załóżmy, że każde pole na planszy należy do kogoś, ale nikt nie wygrał (Rys. 8). Poprzez wierzchołki będziemy rozumieli pola planszy oraz cztery sztucznie dodane wierzchołki reprezentujące każdą stronę planszy. Oznaczmy "sztuczne" wierzchołki przez 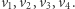 Powiemy, że
Powiemy, że 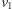 i
i 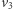 należą do Aldony, a
należą do Aldony, a 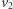 i
i 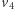 do Bogumiła.
do Bogumiła.
Pokolorujmy każdy wierzchołek  według następującej zasady (Rys. 9):
według następującej zasady (Rys. 9):
- na czarno, jeśli
 należy do Aldony i istnieje ścieżka od
należy do Aldony i istnieje ścieżka od 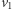 do
do  należąca całkowicie do Aldony,
należąca całkowicie do Aldony, - na szaro, jeśli
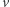 należy do Bogumiła i istnieje ścieżka od
należy do Bogumiła i istnieje ścieżka od 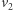 do
do  należąca całkowicie do Bogumiła,
należąca całkowicie do Bogumiła, - na czerwono w przeciwnym wypadku.
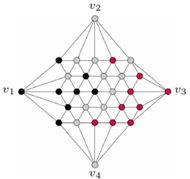
Rys. 9
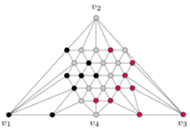
Rys. 10
Wydawałoby się, że nie da się tu użyć lematu Spernera (w końcu graf na rysunku 9 w żadnym stopniu nie przypomina trójkąta). Nie jest to jednak problem, bo możemy go zdeformować, aby uzyskać trójkąt, co widać na rysunku 10 Sprawdźmy, czy powstała triangulacja spełnia warunki lematu Spernera:
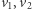 i
i 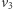 są wierzchołkami powstałego dużego trójkąta i są odpowiednio czarne, szare i czerwone (gdyby
są wierzchołkami powstałego dużego trójkąta i są odpowiednio czarne, szare i czerwone (gdyby 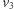 było czarne, to istniałaby ścieżka od
było czarne, to istniałaby ścieżka od 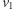 do
do 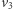 należąca do Aldony - sprzeczność z założeniem o remisie).
należąca do Aldony - sprzeczność z założeniem o remisie).- Na lewym boku dużego trójkąta znajdują się
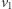 i
i 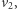 które są odpowiednio czarne i szare. Jest też lewy górny róg planszy. Jest on połączony z
które są odpowiednio czarne i szare. Jest też lewy górny róg planszy. Jest on połączony z 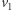 i
i 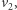 zatem jeśli należy do Aldony, to jest czarny, a jeśli należy do Bogumiła, to jest szary. Nie ma więc koloru czerwonego.
zatem jeśli należy do Aldony, to jest czarny, a jeśli należy do Bogumiła, to jest szary. Nie ma więc koloru czerwonego. - Na prawym boku dużego trójkąta znajdują się
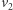 i
i 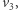 które są odpowiednio szare i czerwone. Jest też prawy górny róg planszy. Gdyby był czarny, to istniałaby ścieżka od
które są odpowiednio szare i czerwone. Jest też prawy górny róg planszy. Gdyby był czarny, to istniałaby ścieżka od 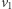 do
do 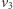 w całości należąca do Aldony - sprzeczność. Nie ma więc koloru czarnego.
w całości należąca do Aldony - sprzeczność. Nie ma więc koloru czarnego. - Na dolnym boku dużego trójkąta znajdują się:
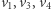 oraz rogi planszy. Wierzchołek
oraz rogi planszy. Wierzchołek 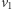 jest czarny, a
jest czarny, a 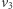 czerwony. Gdyby
czerwony. Gdyby 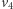 lub któryś z rogów planszy był szary, to istniałaby ścieżka od
lub któryś z rogów planszy był szary, to istniałaby ścieżka od 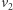 do dolnej krawędzi planszy należąca tylko do Bogumiła - sprzeczność. Nie ma więc koloru szarego.
do dolnej krawędzi planszy należąca tylko do Bogumiła - sprzeczność. Nie ma więc koloru szarego.
Widzimy zatem, że ta triangulacja spełnia warunki lematu i istnieje różnokolorowy mały trójkąt. Oznaczmy przez 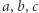 jego wierzchołki, które są odpowiednio czarne, szare i czerwone. Jeśli
jego wierzchołki, które są odpowiednio czarne, szare i czerwone. Jeśli  należy do Aldony, to ponieważ istnieje ścieżka od
należy do Aldony, to ponieważ istnieje ścieżka od 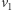 do
do 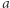 należąca do Aldony, to istnieje także ścieżka od
należąca do Aldony, to istnieje także ścieżka od 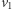 do
do  należąca do Aldony. Zatem
należąca do Aldony. Zatem  powinno być czarne - sprzeczność. Podobnie sprzeczność uzyskujemy, gdy
powinno być czarne - sprzeczność. Podobnie sprzeczność uzyskujemy, gdy  należy do Bogumiła, co kończy dowód.
należy do Bogumiła, co kończy dowód.