Raz, dwa, trzy, wychodź ty!
Dawno temu... w czasach bez Internetu, bez gier komputerowych i smartfonów dzieci bawiły się w chowanego. Na początku zabawy trzeba było oczywiście wyznaczyć osobę, która będzie szukać. Uczestnicy ustawiali się w koło i ktoś odliczał: Raz, dwa, trzy, wychodź ty, i wówczas szósta osoba (odliczanka ma 6 sylab) wychodziła z kółka. Procedurę tę powtarzano aż do momentu, gdy w kółku pozostała jedna osoba - to był pierwszy szukający. Istnieje wiele wierszyków-odliczanek. Moją ulubioną jest odliczanka 15-sylabowa: Mama daje jeść, tata daje pić, a ty sobie idź.
Bardzo dawno temu... dokładniej prawie 2 tysiące lat temu, Flawiusz wraz z grupą powstańców został otoczony w jaskini. Powstańcy zdecydowali, że nie poddadzą się i nie dadzą się pojmać żywcem. Postanowili więc losować: "w jakiej kolejności mamy jeden drugiego zabijać. Pierwszy, na którego padnie, niech zginie z ręki następującego po nim" (cytat z dzieła Flawiusza). W opisie nie było szczegółów na temat losowania i wątpię, czy historyk myślał o jakimkolwiek matematycznym aspekcie tego zagadnienia. Jako pierwszy matematyczną postać temu zdarzeniu nadał francuski matematyk Claude Gaspar Bachet de Méziriac (1581-1638). Według niego powstańcy po ustawieniu się w okrąg mieli eliminować co trzeciego spośród siebie. Nie wiadomo, ilu było powstańców, niektóre źródła podają, że czterdziestu (wraz z Flawiuszem), inne, że czterdziestu jeden. Można też spotkać wersję z co siódmym eliminowanym uczestnikiem "śmiertelnej odliczanki".
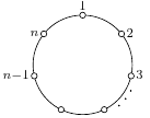
Rys. 1.
Załóżmy, że liczby od  do
do 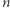 ustawiono na okręgu (patrz Rys. 1). Posuwając się zgodnie z ruchem wskazówek zegara, skreślamy co
ustawiono na okręgu (patrz Rys. 1). Posuwając się zgodnie z ruchem wskazówek zegara, skreślamy co 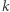 -tą liczbę. Oczywiście w kolejnym okrążeniu nie uwzględniamy w odliczance skreślonych wcześniej liczb. Zajmiemy się problemem szukania ostatniej nieskreślonej liczby spośród
-tą liczbę. Oczywiście w kolejnym okrążeniu nie uwzględniamy w odliczance skreślonych wcześniej liczb. Zajmiemy się problemem szukania ostatniej nieskreślonej liczby spośród 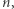 gdy wykreślamy co
gdy wykreślamy co 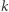 -tą. Oznaczmy ją przez
-tą. Oznaczmy ją przez 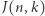 i nazwijmy liczbą szczęśliwą. Zagadnienie to nosi nazwę problemu Flawiusza (Josephus Problem). Spójrzmy na kolejne skreślenia dla
i nazwijmy liczbą szczęśliwą. Zagadnienie to nosi nazwę problemu Flawiusza (Josephus Problem). Spójrzmy na kolejne skreślenia dla 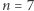 oraz
oraz 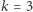 :
:

Wynika stąd, że 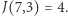
Jak obliczać 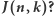 Oczywiście wartości można wyznaczać "ręcznie", ale dla większych
Oczywiście wartości można wyznaczać "ręcznie", ale dla większych 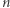 jest to niewygodne. Napiszmy program do obliczania liczb szczęśliwych. Poniżej prezentujemy procedurę napisaną w programie MATHEMATICA (ilustrujemy ją przykładem dla
jest to niewygodne. Napiszmy program do obliczania liczb szczęśliwych. Poniżej prezentujemy procedurę napisaną w programie MATHEMATICA (ilustrujemy ją przykładem dla 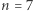 oraz
oraz  ).
).

Wartości 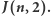 Spójrzmy na tabelkę, w której zamieszczono liczby szczęśliwe dla
Spójrzmy na tabelkę, w której zamieszczono liczby szczęśliwe dla 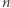 w zakresie od 1 do 20, gdy skreślamy co drugą liczbę:
w zakresie od 1 do 20, gdy skreślamy co drugą liczbę:

Prawidłowość jest ewidentna. Można nawet pokusić się o odgadnięcie wzoru jawnego:
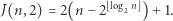 |
(*) |
W dowodzie wzoru 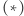 korzysta się z dwóch zależności rekurencyjnych:
korzysta się z dwóch zależności rekurencyjnych:
 |
Okazuje się, że jawny wzór na  jest znany jedynie dla
jest znany jedynie dla 
 dla
dla 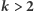 - problem otwarty. Spójrzmy na poniższą tabelkę:
- problem otwarty. Spójrzmy na poniższą tabelkę:

Wartości 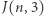 są przedstawione obok dla
są przedstawione obok dla  Można dostrzec następującą prawidłowość: od
Można dostrzec następującą prawidłowość: od 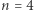 występują "bloki" coraz dłuższych ciągów arytmetycznych o przyroście 3.
występują "bloki" coraz dłuższych ciągów arytmetycznych o przyroście 3.
Pójdźmy jeszcze tropem wyznaczonym przez Andrew M. Odlyzko oraz Herberta S. Wilfa, którzy w pracy [1] z 1991 roku zaproponowali następujący wzór:
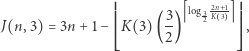 |
gdzie 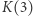 jest stałą (obliczoną za pomocą dość skomplikowanej procedury), której wartość do 9-go miejsca po przecinku wynosi 1,622705028. Jawny wzór, nieodwołujący się do żadnych innych procedur, dla
jest stałą (obliczoną za pomocą dość skomplikowanej procedury), której wartość do 9-go miejsca po przecinku wynosi 1,622705028. Jawny wzór, nieodwołujący się do żadnych innych procedur, dla  gdy
gdy 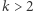 nie jest znany.
nie jest znany.
Inny trop, permutacje - i zaskakująca puenta. Pewne zastosowanie problemu Flawiusza można znaleźć w książce Israela N. Hersteina i Irvinga Kaplansky'ego Matters Mathematical [2]. Autorzy używają tak zwanych permutacji Josephusa. Wyjaśnimy to na przykładzie 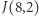 : w ręcznym wykreślaniu eliminowane są kolejno 2, 4, 6, 8, 3, 7, 5. Na końcu ciągu dopiszmy nieskreślone 1. Kolejność skreślania można zapisać w postaci permutacji
: w ręcznym wykreślaniu eliminowane są kolejno 2, 4, 6, 8, 3, 7, 5. Na końcu ciągu dopiszmy nieskreślone 1. Kolejność skreślania można zapisać w postaci permutacji
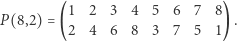 |
Każdą permutację możemy przedstawić w postaci rozłącznych cykli, w naszym przypadku:  Analogicznie można postąpić dla dowolnego
Analogicznie można postąpić dla dowolnego 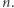 Herstein i Kaplansky odkryli, że jeśli
Herstein i Kaplansky odkryli, że jeśli  oraz
oraz 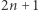 są liczbami pierwszymi oraz
są liczbami pierwszymi oraz  jest postaci
jest postaci  to permutacja
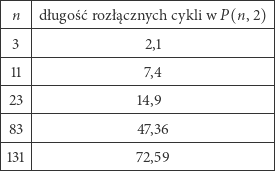
to permutacja 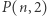 jest iloczynem dwóch rozłącznych cykli. Długości tych cykli dla wybranych
jest iloczynem dwóch rozłącznych cykli. Długości tych cykli dla wybranych 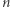 umieszczono w tabelce poniżej.
umieszczono w tabelce poniżej.
Zanim opiszemy kolejne odkrycie Hersteina i Kaplansky'ego, przedstawimy kilka informacji dotyczących ciał liczbowych. Czytelnicy doskonale znają liczby wymierne oraz ich bogatą strukturę algebraiczną - z dodawaniem i odejmowaniem, mnożeniem i dzieleniem zbiór 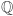 tworzy ciało. A co się stanie, gdy rozszerzymy zbiór
tworzy ciało. A co się stanie, gdy rozszerzymy zbiór 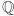 o jakiś element niebędący liczbą wymierną? Powinniśmy przy tym zadbać, aby algebraicznie nowy zbiór nic nie "stracił", to znaczy pozostał ciałem. Przykład takiego rozszerzenia podał Gauss, jest to ciało Gaussa:
o jakiś element niebędący liczbą wymierną? Powinniśmy przy tym zadbać, aby algebraicznie nowy zbiór nic nie "stracił", to znaczy pozostał ciałem. Przykład takiego rozszerzenia podał Gauss, jest to ciało Gaussa: 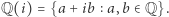 Z kolei o pierścieniu Gaussa
Z kolei o pierścieniu Gaussa 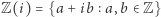 można powiedzieć, że jest tym dla ciała
można powiedzieć, że jest tym dla ciała 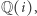 czym dla
czym dla 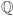 są liczby całkowite
są liczby całkowite 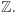 Kluczowa własność zbioru liczb całkowitych to rozkładalność na czynniki pierwsze i jednoznaczność tego rozkładu. Okazuje się, że w pierścieniu Gaussa liczby także są jednoznacznie rozkładalne na czynniki pierwsze.
Kluczowa własność zbioru liczb całkowitych to rozkładalność na czynniki pierwsze i jednoznaczność tego rozkładu. Okazuje się, że w pierścieniu Gaussa liczby także są jednoznacznie rozkładalne na czynniki pierwsze.
Pojęciem ogólniejszym od ciała Gaussa są ciała liczbowe postaci 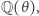 gdzie
gdzie 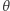 jest liczbą algebraiczną (czyli pierwiastkiem wielomianu o współczynnikach całkowitych). Ciało Gaussa jest ciałem liczbowym,
jest liczbą algebraiczną (czyli pierwiastkiem wielomianu o współczynnikach całkowitych). Ciało Gaussa jest ciałem liczbowym, 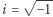 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu  Dla ciał liczbowych rozpatruje się pierścienie "liczb całkowitych" tych ciał i bada własność jednoznaczności rozkładu tych pierścieni. Ta własność ma fundamentalne znaczenie przy rozwiązywaniu równań diofantycznych, na przykład równania Fermata
Dla ciał liczbowych rozpatruje się pierścienie "liczb całkowitych" tych ciał i bada własność jednoznaczności rozkładu tych pierścieni. Ta własność ma fundamentalne znaczenie przy rozwiązywaniu równań diofantycznych, na przykład równania Fermata 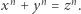 Batalia o dowód, że równanie Fermata nie ma rozwiązań w dodatnich liczbach całkowitych dla każdego
Batalia o dowód, że równanie Fermata nie ma rozwiązań w dodatnich liczbach całkowitych dla każdego 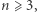 zakończyła się dla wielu wybitnych matematyków klęską. Przyjmowali oni bowiem błędne założenie, że pewne pierścienie mają własność jednoznaczności rozkładu.
zakończyła się dla wielu wybitnych matematyków klęską. Przyjmowali oni bowiem błędne założenie, że pewne pierścienie mają własność jednoznaczności rozkładu.
Jeśli 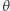 jest pierwiastkiem wielomianu kwadratowego o współczynnikach całkowitych, to możemy zakładać, że
jest pierwiastkiem wielomianu kwadratowego o współczynnikach całkowitych, to możemy zakładać, że 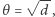 gdzie
gdzie 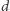 jest bezkwadratową liczbą całkowitą. Wówczas pierścień liczb całkowitych ciała
jest bezkwadratową liczbą całkowitą. Wówczas pierścień liczb całkowitych ciała 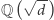 to po prostu
to po prostu 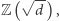 wtedy gdy
wtedy gdy 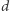 jest postaci
jest postaci 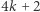 lub
lub 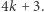 Natomiast dla liczb postaci
Natomiast dla liczb postaci 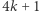 ten pierścień to
ten pierścień to 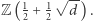
Przykładem pierścienia, w którym nie ma jednoznaczności rozkładu, jest 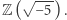 W pierścieniu tym mamy na przykład
W pierścieniu tym mamy na przykład  Aby badać problem jednoznaczności rozkładu w pierścieniach typu
Aby badać problem jednoznaczności rozkładu w pierścieniach typu 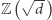 lub
lub 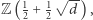 wprowadzono pojęcie liczby klas. Liczba klas ciała służy do rozpoznawania, czy wspomniane pierścienie mają własność jednoznaczności rozkładu, co zachodzi wtedy i tylko wtedy, gdy liczba klas jest równa 1. Udowodniono, że istnieje dokładnie dziewięć pierścieni ciał liczbowych
wprowadzono pojęcie liczby klas. Liczba klas ciała służy do rozpoznawania, czy wspomniane pierścienie mają własność jednoznaczności rozkładu, co zachodzi wtedy i tylko wtedy, gdy liczba klas jest równa 1. Udowodniono, że istnieje dokładnie dziewięć pierścieni ciał liczbowych  gdzie
gdzie 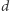 jest bezkwadratową ujemną liczbą całkowitą, mających własność jednoznaczności rozkładu. Te liczby to: -1, -2, -3, -7, -11, -19, -43, -67, -163.
jest bezkwadratową ujemną liczbą całkowitą, mających własność jednoznaczności rozkładu. Te liczby to: -1, -2, -3, -7, -11, -19, -43, -67, -163.
Powróćmy teraz do permutacji Josephusa. Przypomnijmy, że rozważamy takie 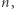 że
że  oraz
oraz  są liczbami pierwszymi oraz
są liczbami pierwszymi oraz 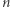 jest postaci
jest postaci 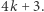 Okazało się, że długości cykli można wykorzystać do obliczania liczby klas niektórych ciał liczbowych postaci
Okazało się, że długości cykli można wykorzystać do obliczania liczby klas niektórych ciał liczbowych postaci 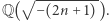 W każdym takim ciele pierścień liczb całkowitych to
W każdym takim ciele pierścień liczb całkowitych to 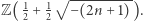 I tutaj niespodzianka: liczbę klas ciała
I tutaj niespodzianka: liczbę klas ciała 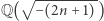 można wyznaczyć, korzystając z długości cykli zamieszczonych w tabeli 1. Liczba klas ciała
można wyznaczyć, korzystając z długości cykli zamieszczonych w tabeli 1. Liczba klas ciała 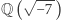 (czyli
(czyli 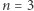 ) wynosi
) wynosi 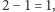 liczba klas ciała
liczba klas ciała 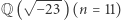 wynosi
wynosi 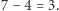 Dla ciała
Dla ciała 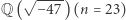 mamy liczbę klas
mamy liczbę klas  i tak dalej.
i tak dalej.
Przedstawiliśmy zadanie, problem Flawiusza, które ma już ponad 400 lat (de Méziriac opublikował je w książce wydanej w 1612 roku), ale wciąż wzbudza spore zainteresowanie. Mnóstwo informacji na ten temat można znaleźć w Matematyce konkretnej [3]. Zachęcamy do zapoznania się z tą piękną książką, zawierającą mnóstwo interesujących faktów dotyczących rozpatrywanych tu zagadnień.
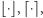 nazywane odpowiednio podłoga i sufit, zaokrąglają liczby rzeczywiste do liczb całkowitych odpowiednio w dół i w górę.
nazywane odpowiednio podłoga i sufit, zaokrąglają liczby rzeczywiste do liczb całkowitych odpowiednio w dół i w górę.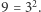
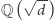 to pojęcie związane z funkcjami postaci
to pojęcie związane z funkcjami postaci 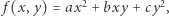 gdzie
gdzie  Bierzemy zbiór wszystkich takich funkcji (często używa się nazwy forma kwadratowa dwóch zmiennych) o ustalonym wyróżniku
Bierzemy zbiór wszystkich takich funkcji (często używa się nazwy forma kwadratowa dwóch zmiennych) o ustalonym wyróżniku 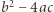 i wprowadzamy pewną relację równoważności w tym zbiorze. Relacja ta dzieli rozpatrywany zbiór na rozłączne klasy abstrakcji. Klas tych jest zawsze skończenie wiele, a ich liczbę nazywamy liczbą klas ciała liczbowego.
i wprowadzamy pewną relację równoważności w tym zbiorze. Relacja ta dzieli rozpatrywany zbiór na rozłączne klasy abstrakcji. Klas tych jest zawsze skończenie wiele, a ich liczbę nazywamy liczbą klas ciała liczbowego.