Parkietaże
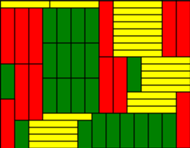
W autorskim tygodniku internetowym Trapez Jarosław Wróblewski proponuje serię zadań (nr 75-126) o parkietowaniu prostokątów. Na przykład: czy planszę 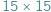 da się szczelnie pokryć klockami o wymiarach
da się szczelnie pokryć klockami o wymiarach 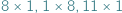 oraz
oraz 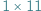 (oczywiście klocki nie mogą na siebie zachodzić).
(oczywiście klocki nie mogą na siebie zachodzić).
W tego typu zadaniach odpowiedź zazwyczaj brzmi "nie", a typowa strategia polega na zgadnięciu numeracji lub kolorowania pól planszy i użyciu argumentu w stylu "każdy klocek pokrywa trzy pola zielone, ale liczba pól zielonych na całej planszy jest niepodzielna przez 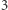 ". Spróbujmy jednak ogólniej zastanowić się, jak systematycznie, od podstaw, można zaatakować problem: czy planszę o wymiarach
". Spróbujmy jednak ogólniej zastanowić się, jak systematycznie, od podstaw, można zaatakować problem: czy planszę o wymiarach 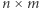 da się wyparkietować klockami ustalonych typów
da się wyparkietować klockami ustalonych typów 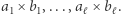
Niech 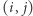 oznacza pole w
oznacza pole w 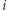 -tym wierszu i
-tym wierszu i 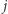 -tej kolumnie. Każde pokrycie planszy możemy zakodować za pomocą zmiennych
-tej kolumnie. Każde pokrycie planszy możemy zakodować za pomocą zmiennych
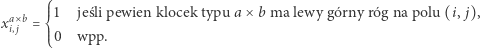 |
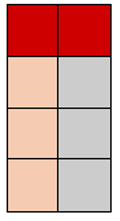
Przykład parkietażu
Na przykład pokrycie planszy  z rysunku obok opisujemy następująco:
z rysunku obok opisujemy następująco:
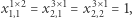
a wszystkie inne zmienne 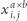 są równe zero.
są równe zero.
Zapytajmy teraz, kiedy zestaw zmiennych 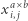 opisuje poprawny parkietaż. Przede wszystkim musimy usunąć wszystkie zmienne
opisuje poprawny parkietaż. Przede wszystkim musimy usunąć wszystkie zmienne
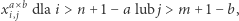
ponieważ klocek o wymiarach 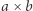 z lewym górnym rogiem na polu
z lewym górnym rogiem na polu 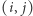 wystawałby poza planszę. Po drugie, wszystkie zmienne muszą przyjmować wartości 0 lub
wystawałby poza planszę. Po drugie, wszystkie zmienne muszą przyjmować wartości 0 lub 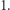 W końcu, musimy zagwarantować, że każde pole planszy jest pokryte przez dokładnie jeden klocek. Ten warunek można zapisać następująco:
W końcu, musimy zagwarantować, że każde pole planszy jest pokryte przez dokładnie jeden klocek. Ten warunek można zapisać następująco:
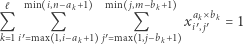 |
(1) |
dla każdego 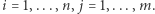 Ten nieprzyjemny wzór oznacza po prostu, że spośród wszystkich legalnych położeń dostępnych klocków, które potencjalnie mogą zahaczać o pole
Ten nieprzyjemny wzór oznacza po prostu, że spośród wszystkich legalnych położeń dostępnych klocków, które potencjalnie mogą zahaczać o pole 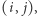 dokładnie jedno jest faktycznie w użyciu. A zatem zerojedynkowe rozwiązania układu
dokładnie jedno jest faktycznie w użyciu. A zatem zerojedynkowe rozwiązania układu 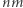 równań liniowych (1) odpowiadają jednoznacznie parkietażom.
równań liniowych (1) odpowiadają jednoznacznie parkietażom.
Dla zupełnej jasności rozważmy przykład. Zapiszmy w tym języku problem parkietowania planszy 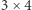 klockami typu
klockami typu 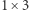 i
i 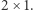 Mamy
Mamy 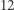 równań, z których każde wymienia legalne sposoby pokrycia jednego z pól:
równań, z których każde wymienia legalne sposoby pokrycia jednego z pól:
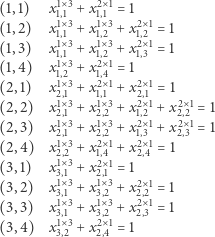 |
(2) |
Na przykład równanie dla pola 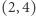 czytamy następująco: pole to można przykryć klockiem
czytamy następująco: pole to można przykryć klockiem 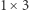 z pola
z pola 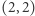 lub klockiem
lub klockiem 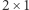 z jednego z pól
z jednego z pól 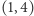 lub
lub 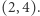
Jak łatwo sprawdzić, prostokąta 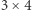 klockami
klockami 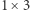 i
i 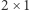 pokryć się nie da. Możemy tego faktu dowieść algebraicznie, mianowicie mnożąc równania (2) kolejno przez następujące współczynniki:
pokryć się nie da. Możemy tego faktu dowieść algebraicznie, mianowicie mnożąc równania (2) kolejno przez następujące współczynniki:
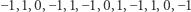 |
(3) |
i dodając wszystko stronami. Wtedy otrzymamy
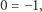
co dowodzi, że układ (2) nie ma rozwiązań rzeczywistych (a więc tym bardziej zerojedynkowych!).
Uogólnijmy ostatnie rozumowanie. Układ równań liniowych nie ma rozwiązań w liczbach rzeczywistych jedynie wówczas, gdy pewna kombinacja liniowa danych równań daje "oczywistą sprzeczność" postaci "zero z lewej, coś niezerowego z prawej strony". Nie udowodnimy tego faktu, a jedynie odwołamy się do intuicji i życiowego doświadczenia Czytelników w tym zakresie.
Co to znaczy w szczególnym przypadku układu (1)? Oznaczmy przez 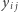 współczynnik, przez jaki w naszym dowodzie nierozwiązywalności przemnożymy równanie dla pola
współczynnik, przez jaki w naszym dowodzie nierozwiązywalności przemnożymy równanie dla pola 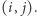 Możemy nawet myśleć o tych współczynnikach jako wpisanych w pola planszy:
Możemy nawet myśleć o tych współczynnikach jako wpisanych w pola planszy: 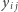 umieszczamy na polu
umieszczamy na polu 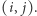 Na przykład współczynniki (3) dla przykładu (2) pojawią się na planszy
Na przykład współczynniki (3) dla przykładu (2) pojawią się na planszy 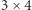 w następującej kolejności:
w następującej kolejności:
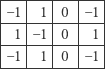 |
Wtedy (proszę sprawdzić) "oczywista sprzeczność" dla układu (1) polega na tym, że:
- każde dopuszczalne położenie klocka na planszy pokrywa pola o sumie
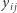 równej zeru,
równej zeru, - suma wszystkich
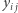 jest niezerowa.
jest niezerowa.
Jest zupełnie Jasne (przez duże J, i to bez lektury całego naszego wywodu), że powyższe warunki dowodzą nieistnienia parkietażu! A zatem odkryliśmy od podstaw jeden z wariantów magicznej metody rozwiązywania tego typu zadań, wspomnianej na początku.

Spójrzmy na to, co tutaj się stało, z jeszcze szerszej perspektywy. Układ równań taki jak (1) jest bardzo szczególnym przypadkiem problemu z zakresu programowania całkowitoliczbowego (ang. mixed-integer programming). Wiele trudnych problemów kombinatorycznych można zakodować w tej postaci, wprowadzając zmienne zerojedynkowe opisujące pewne zdarzenia (np. klocek leży na polu) i wyrażając wzajemne ograniczenia (np. klocki nie zachodzą na siebie) w postaci równań i nierówności liniowych, tak jak w (1). Jest to standardowa technika dla wielu tego typu problemów. Rozwiązywanie problemów całkowitoliczbowych, choć możliwe, jest bardzo czasochłonne (w istocie NP-trudne), dlatego możemy na początek zapytać, czy badany problem ma w ogóle rozwiązanie w liczbach rzeczywistych. Ten proces nazywa się relaksacją. Powstały problem liniowy można rozwiązać efektywnie, a jeżeli okaże się, że rozwiązania nie ma, to zawsze można podać certyfikat niespełnialności (ang. infeasibility certificate), analogiczny do naszej tabeli współczynników 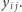 Czytelnikom zainteresowanym tym Olbrzymim (przez duże O) działem optymalizacji proponuję wpisanie wymienionych tu haseł w wyszukiwarce. Reasumując:
Czytelnikom zainteresowanym tym Olbrzymim (przez duże O) działem optymalizacji proponuję wpisanie wymienionych tu haseł w wyszukiwarce. Reasumując:
dowód nieistnienia parkietażu przez kolorowanie/numerowanie i inne sprytne niezmienniki
to nic innego, jak
certyfikat niespełnialności dla liniowej relaksacji całkowitoliczbowego modelu parkietowania.
Pod tym adresem można znaleźć kod źródłowy wraz z komentarzami, pozwalający własnoręcznie eksperymentować z parkietażami przy użyciu ogólnodostępnych pakietów do modelowania i programowania liniowego/całkowitoliczbowego. Można tam znaleźć rozwiązanie zadania o planszy 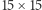 ze wstępu.
ze wstępu.