Teoria grup w kombinatoryce
Ten artykuł będzie poświęcony zliczaniu różnych kolorowań obiektów, które podlegają symetrii. Wyobraźmy sobie, że Kalina chciałaby pokolorować rogi kwadratu za pomocą 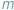 kolorów. Ile różnych figur może w ten sposób otrzymać?
kolorów. Ile różnych figur może w ten sposób otrzymać?
Poniższy rysunek przedstawia wszystkie możliwe kolorowania dwoma kolorami, podzielone na zbiory kolorowań identycznych względem izometrii.
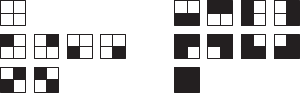
Jak widać istnieje 16 kolorowań dwoma kolorami, ale tylko 6, gdy dopuścimy obracanie kwadratem i odbicia symetryczne. Aby obliczyć liczbę kolorowań większą liczbą kolorów, przyjrzyjmy się dokładnie izometriom naszego obiektu.
W przypadku kwadratu jest ich 8:
- identyczność,
- obroty o
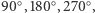
- odbicia względem przekątnych, osi pionowej oraz osi poziomej.
Dodatkowo izometrie dowolnego obiektu można składać. Oznaczmy tę operację 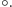 Przykładowo: jeżeli odbijemy kwadrat względem osi pionowej, a następnie obrócimy go o
Przykładowo: jeżeli odbijemy kwadrat względem osi pionowej, a następnie obrócimy go o 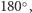 otrzymamy odbicie względem osi poziomej. Zbiór izometrii wraz z operacją
otrzymamy odbicie względem osi poziomej. Zbiór izometrii wraz z operacją  ma poniższe podstawowe własności, dzięki którym tworzą one grupę, którą od teraz będziemy oznaczać przez
ma poniższe podstawowe własności, dzięki którym tworzą one grupę, którą od teraz będziemy oznaczać przez 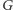
- złożenie dowolnych dwóch izometrii również jest izometrią;
- działanie
 jest łączne, czyli dla dowolnych
jest łączne, czyli dla dowolnych 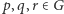 mamy
mamy 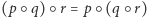 ;
; - istnieje element neutralny
 nazywany identycznością, taki że dla dowolnego
nazywany identycznością, taki że dla dowolnego 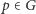 zachodzi
zachodzi 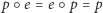 ;
; - dla dowolnego
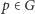 istnieje izometria odwrotna nazywana
istnieje izometria odwrotna nazywana 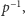 taka że
taka że 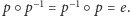
Zachęcam Czytelnika, aby samodzielnie uzasadnił powyższe własności grupy izometrii.
Jeżeli oznaczymy teraz zbiór wszystkich kolorowań kwadratu 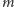 kolorami (dla pewnego ustalonego
kolorami (dla pewnego ustalonego 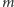 ) przez
) przez 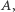 będziemy mogli zdefiniować działanie grupy
będziemy mogli zdefiniować działanie grupy 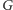 na zbiór
na zbiór 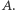 Zauważmy, że dowolna symetria
Zauważmy, że dowolna symetria 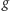 z
z 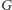 może działać na każdy element z
może działać na każdy element z 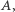 przekształcając go na pewien inny. Mówiąc formalnie, jest to funkcja spełniająca dwie własności:
przekształcając go na pewien inny. Mówiąc formalnie, jest to funkcja spełniająca dwie własności:
Aby lepiej zrozumieć działanie grupy izometrii na kolorowaniach obiektu, warto przyjrzeć się rysunkowi kolorowań kwadratu i zastanowić się, którymi izometriami trzeba działać na kolorowania z każdej grupy, aby otrzymać pozostałe.
Zanim przejdziemy do kluczowego twierdzenia, potrzebujemy jeszcze trzech nowych pojęć. Dla dowolnej izometrii 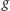 zbiorem jej punktów stałych będą wszystkie kolorowania
zbiorem jej punktów stałych będą wszystkie kolorowania 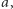 takie że
takie że 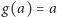 - będziemy ten zbiór oznaczać przez
- będziemy ten zbiór oznaczać przez 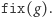 Dla dowolnego kolorowania
Dla dowolnego kolorowania 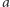 zbiorem jego stabilizatorów będą wszystkie symetrie
zbiorem jego stabilizatorów będą wszystkie symetrie 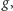 takie że
takie że 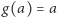 - ten zbiór będziemy oznaczać przez
- ten zbiór będziemy oznaczać przez 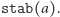 Ostatecznie, dla pewnego kolorowania
Ostatecznie, dla pewnego kolorowania 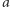 orbitą, do której ono należy, będzie zbiór wszystkich innych kolorowań, które można otrzymać z
orbitą, do której ono należy, będzie zbiór wszystkich innych kolorowań, które można otrzymać z  działając pewną izometrią z
działając pewną izometrią z 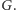 Ten zbiór będziemy nazywać
Ten zbiór będziemy nazywać 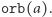 Zauważmy teraz, że na rysunku wszystkich kolorowań kwadratu (poprzednia strona) zostały one podzielone właśnie na orbity. Każda orbita odpowiada jednemu sposobowi kolorowania obiektu, zatem naszym celem jest obliczenie ich liczby.
Zauważmy teraz, że na rysunku wszystkich kolorowań kwadratu (poprzednia strona) zostały one podzielone właśnie na orbity. Każda orbita odpowiada jednemu sposobowi kolorowania obiektu, zatem naszym celem jest obliczenie ich liczby.
Niech 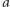 oraz
oraz 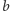 będą dwoma kolorowaniami należącymi do tej samej orbity. Ponadto niech
będą dwoma kolorowaniami należącymi do tej samej orbity. Ponadto niech 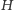 oznacza zbiór wszystkich takich izometrii
oznacza zbiór wszystkich takich izometrii 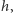 że
że 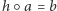 ; zauważmy również, że
; zauważmy również, że 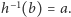 Wybierzmy dowolną izometrię
Wybierzmy dowolną izometrię 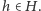 Składając ją lewostronnie ze wszystkimi izometriami ze zbioru
Składając ją lewostronnie ze wszystkimi izometriami ze zbioru 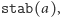 otrzymamy
otrzymamy 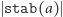 różnych izometrii należących do
różnych izometrii należących do 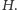 Zatem
Zatem 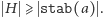 Ponadto
Ponadto 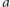 można składać z odwrotnościami wszystkich izometrii z
można składać z odwrotnościami wszystkich izometrii z 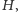 otrzymując
otrzymując 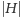 izometrii należących do
izometrii należących do 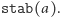 Z tego wynika, że
Z tego wynika, że 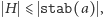 więc:
więc:

Jeżeli zadziałamy na kolorowanie 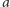 wszystkimi izometriami z
wszystkimi izometriami z 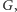 to każde z kolorowań ze zbioru
to każde z kolorowań ze zbioru 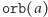 otrzymamy dokładnie tyle samo razy w wyniku działania grupy. Można zatem wywnioskować bardzo ważny lemat:
otrzymamy dokładnie tyle samo razy w wyniku działania grupy. Można zatem wywnioskować bardzo ważny lemat:

Teraz jesteśmy gotowi, aby wyprowadzić kluczowy wzór. Oznaczając zbiór wszystkich orbit poprzez 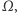 otrzymujemy:
otrzymujemy:

Ostatnia równość wynika z faktu, że zarówno 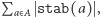 jak i
jak i 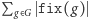 są równe liczbie par
są równe liczbie par 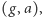 takich że
takich że 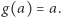 Wyprowadzona powyżej tożsamość nazywana jest lematem Burnside'a. Zbiór
Wyprowadzona powyżej tożsamość nazywana jest lematem Burnside'a. Zbiór 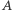 jest niejednokrotnie ogromny, przez co nie ma możliwości badania wszystkich orbit. Dzięki tej równości wystarczy sklasyfikować izometrie z grupy
jest niejednokrotnie ogromny, przez co nie ma możliwości badania wszystkich orbit. Dzięki tej równości wystarczy sklasyfikować izometrie z grupy 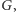 których jest stosunkowo niewiele. Jedyną trudnością, jaka pozostała, jest obliczenie dla każdej izometrii, ile ma ona punktów stałych. Aby to zrobić, musimy spojrzeć, które spośród rogów kwadratu dana izometria przekształca na które. W ten sposób rozbijemy je na cykle, a każdy z nich będzie musiał być w tym samym kolorze. Jeżeli izometria ma
których jest stosunkowo niewiele. Jedyną trudnością, jaka pozostała, jest obliczenie dla każdej izometrii, ile ma ona punktów stałych. Aby to zrobić, musimy spojrzeć, które spośród rogów kwadratu dana izometria przekształca na które. W ten sposób rozbijemy je na cykle, a każdy z nich będzie musiał być w tym samym kolorze. Jeżeli izometria ma 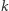 cykli, to ma ona
cykli, to ma ona 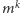 punktów stałych, ponieważ każdy z nich kolorujemy jednym kolorem.
punktów stałych, ponieważ każdy z nich kolorujemy jednym kolorem.
Dla ułatwienia ponumerujmy rogi kwadratu od 1 do 4 tak, jak numeruje się ćwiartki układu współrzędnych. Poniższa tabela przedstawia, jakie cykle powstaną dla wszystkich izometrii kwadratu. Zachęcam do jej dokładnego przeanalizowania.
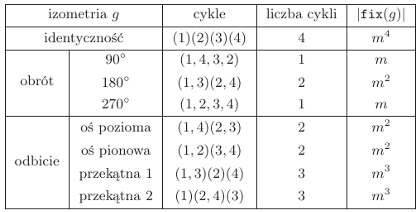
Podsumowując dane z tabeli i wstawiając je do otrzymanego wzoru, możemy wyprowadzić wzór na liczbę różnych kolorowań kwadratu 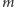 kolorami:
kolorami:

Spróbujmy teraz zmierzyć się z trudniejszym problemem. Wyobraźmy sobie, że Kalina chciałaby pokolorować wszystkie ściany sześciennej kostki, mając do dyspozycji kredki w  kolorach. Ile różnych kostek mogłaby w ten sposób otrzymać? Tym razem nie będziemy wypisywać wszystkich izometrii sześcianu, musimy to zrobić sprytniej. Zacznijmy od tego, że obracając sześcian, możemy go postawić na dowolnej ze ścian, a następnie obrócić na cztery sposoby, zatem mamy
kolorach. Ile różnych kostek mogłaby w ten sposób otrzymać? Tym razem nie będziemy wypisywać wszystkich izometrii sześcianu, musimy to zrobić sprytniej. Zacznijmy od tego, że obracając sześcian, możemy go postawić na dowolnej ze ścian, a następnie obrócić na cztery sposoby, zatem mamy 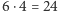 izometrie. Spróbujmy je teraz sklasyfikować.
izometrie. Spróbujmy je teraz sklasyfikować.
- Identyczność. Każda ściana przechodzi sama na siebie, tworząc osobny cykl, zatem ma ona
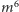 punktów stałych.
punktów stałych. - Obrót o
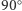 lub
lub 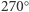 względem osi przechodzącej przez środki przeciwległych ścian. Jest
względem osi przechodzącej przez środki przeciwległych ścian. Jest 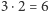 takich izometrii. Dla każdej z nich dwie ściany, przez które przechodzi oś symetrii, przechodzą same na siebie, natomiast pozostałe ściany tworzą jeden cykl, zatem mamy
takich izometrii. Dla każdej z nich dwie ściany, przez które przechodzi oś symetrii, przechodzą same na siebie, natomiast pozostałe ściany tworzą jeden cykl, zatem mamy 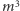 punktów stałych.
punktów stałych. - Obrót o
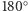 względem osi przechodzącej przez środki przeciwległych ścian. Są trzy takie izometrie. Cykle zachowują się podobnie jak w poprzednim przypadku, ale cykl długości
względem osi przechodzącej przez środki przeciwległych ścian. Są trzy takie izometrie. Cykle zachowują się podobnie jak w poprzednim przypadku, ale cykl długości 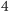 rozbija się na
rozbija się na 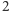 cykle długości
cykle długości 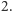 Mamy zatem
Mamy zatem 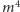 punktów stałych.
punktów stałych. - Obrót o
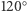 lub o
lub o 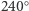 względem osi przechodzącej przez parę przeciwległych wierzchołków. Mamy
względem osi przechodzącej przez parę przeciwległych wierzchołków. Mamy 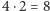 takich izometrii. Każda z nich tworzy dwa cykle długości
takich izometrii. Każda z nich tworzy dwa cykle długości 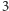 przy obu wierzchołkach, tworząc
przy obu wierzchołkach, tworząc 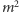 punktów stałych.
punktów stałych. - Obrót o
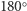 względem osi przechodzącej przez środki przeciwległych krawędzi. Jest
względem osi przechodzącej przez środki przeciwległych krawędzi. Jest 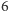 takich izometrii. W każdej z nich
takich izometrii. W każdej z nich 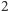 pary ścian połączone krawędziami, przez które przechodzi oś, oraz pozostałe
pary ścian połączone krawędziami, przez które przechodzi oś, oraz pozostałe 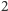 ściany, przechodzą na siebie nawzajem. Mamy trzy cykle długości
ściany, przechodzą na siebie nawzajem. Mamy trzy cykle długości 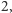 więc jest
więc jest 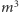 punktów stałych.
punktów stałych.
Zauważmy, że rozpatrzyliśmy już wszystkie 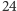 izometrie. Po podstawieniu otrzymanych danych do wzoru otrzymujemy wzór na liczbę nieizometrycznych kolorowań ścian sześcianu
izometrie. Po podstawieniu otrzymanych danych do wzoru otrzymujemy wzór na liczbę nieizometrycznych kolorowań ścian sześcianu 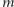 kolorami:
kolorami:

Po przeczytaniu tego artykułu warto spróbować własnych sił i ustalić, na ile sposobów Kalina mogłaby pokolorować czworościan, a na ile ośmiościan foremny za pomocą 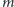 kolorów.
kolorów.