Kombinatoryka ekstremalna i przesuwanie zbiorów
Najogólniej mówiąc, kombinatoryka ekstremalna zajmuje się pytaniami o to, jaki jest rozmiar największego (lub najmniejszego) możliwego zbioru obiektów danego typu, spełniającego pewien zadany warunek i jak takie ekstremalne przypadki wyglądają.
Wiele z nich dotyczy rodzin zbiorów, jak np.
Pytanie 1. Jaka jest największa rodzina podzbiorów zbioru 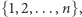 której każde dwa elementy mają niepuste przecięcie?
której każde dwa elementy mają niepuste przecięcie?
Rodzinę spełniającą ten warunek nazywać będziemy przecinającą się. Oznaczmy dla wygody
![[n] = {1,2,...,n}.](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/2x-3d29ab570055ce2273fc84c8103d26f2a48b9fc2-dm-33,33,33-FF,FF,FF.gif)
Nietrudno wskazać przykład sporej rodziny przecinającej się: dla dowolnego ![|a∈ [n]](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/3x-3d29ab570055ce2273fc84c8103d26f2a48b9fc2-im-33,33,33-FF,FF,FF.gif) spełnia ten warunek rodzina wszystkich podzbiorów
spełnia ten warunek rodzina wszystkich podzbiorów ![[n],](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/4x-3d29ab570055ce2273fc84c8103d26f2a48b9fc2-im-33,33,33-FF,FF,FF.gif) które zawierają
które zawierają 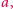 składająca się z
składająca się z 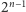 zbiorów.
zbiorów.
Więcej już nie uzyskamy, o czym przekonamy się, ustawiając wszystkie podzbiory zbioru ![|[n]](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/1x-6ce24713b91f2ade87e60c532b48037a6501cd09-im-33,33,33-FF,FF,FF.gif) w
w 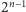 par postaci
par postaci ![{A,[n] ∖ A}.](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/3x-6ce24713b91f2ade87e60c532b48037a6501cd09-im-33,33,33-FF,FF,FF.gif) Dowolna rodzina przecinającą się zawiera co najwyżej jeden zbiór z każdej pary, więc jej liczność nie przekracza
Dowolna rodzina przecinającą się zawiera co najwyżej jeden zbiór z każdej pary, więc jej liczność nie przekracza 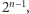 co chcieliśmy wykazać.
co chcieliśmy wykazać.
Po tej udanej rozgrzewce rozważmy podobny problem dla rodzin  -jednorodnych, tzn. składających się tylko ze zbiorów ustalonej mocy
-jednorodnych, tzn. składających się tylko ze zbiorów ustalonej mocy ![|r∈ [n].](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/2x-bfb29e9d36f3728a72389bd0f54ea94d707f7ad1-im-33,33,33-FF,FF,FF.gif)
Taką rodzinę będziemy nazywać w skrócie 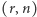 -rodziną. Dla
-rodziną. Dla 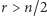 widać, że nawet rodzina wszystkich
widać, że nawet rodzina wszystkich  -elementowych podzbiorów zbioru
-elementowych podzbiorów zbioru ![|[n]](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/6x-acdedc4f239bbe472569338869b742bff0f8930e-im-33,33,33-FF,FF,FF.gif) jest
jest 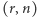 -rodziną, więc w dalszym ciągu zakładamy, że
-rodziną, więc w dalszym ciągu zakładamy, że 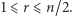
Modyfikując wcześniejszy przykład, możemy wskazać 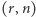 -rodzinę wszystkich
-rodzinę wszystkich  -elementowych podzbiorów
-elementowych podzbiorów ![[n]](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/3x-b062db73b4cfedddc16b3372ff930a7cee9a5594-im-33,33,33-FF,FF,FF.gif) zawierających pewną ustaloną liczbę
zawierających pewną ustaloną liczbę ![a ∈ [n]](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/4x-b062db73b4cfedddc16b3372ff930a7cee9a5594-im-33,33,33-FF,FF,FF.gif) ; rodzina ta liczyć będzie
; rodzina ta liczyć będzie 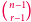 elementów.
elementów.
Podobnie jak wcześniej, więcej się nie da, ale dowód maksymalności jest teraz bardziej wymagający. My skorzystamy z ciekawej i bardzo użytecznej techniki przesuwania (ang. shifting) rodziny zbiorów, która ograniczy nasz problem do dość wygodnych rodzin.
O co chodzi w przesuwaniu? Zakładamy, że dana jest pewna rodzina 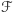 podzbiorów
podzbiorów ![|[n].](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/2x-68dcd0d82a1734ff8e8e589b8243b24a8fdadffe-im-33,33,33-FF,FF,FF.gif) Dla dowolnej pary liczb
Dla dowolnej pary liczb 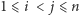 określamy operację
określamy operację 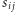 na zbiorach
na zbiorach 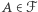 jako "podmianę" liczby
jako "podmianę" liczby 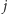 na
na 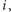 o ile jest to możliwe i o ile prowadzi do powstania zbioru spoza
o ile jest to możliwe i o ile prowadzi do powstania zbioru spoza 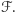 Bardziej precyzyjnie
Bardziej precyzyjnie

Widać, że definicja 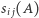 zależy nie tylko od
zależy nie tylko od 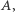 ale też od rodziny
ale też od rodziny 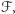 którą rozważamy, więc lepiej byłoby pisać
którą rozważamy, więc lepiej byłoby pisać  zamiast
zamiast 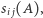 ale na szczęście i tak nie napotkamy na kłopoty w oznaczeniach. Stosując ją, zastępujemy pewne wystąpienia liczby
ale na szczęście i tak nie napotkamy na kłopoty w oznaczeniach. Stosując ją, zastępujemy pewne wystąpienia liczby 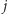 w zbiorach rodziny
w zbiorach rodziny 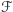 wystąpieniami mniejszej liczby
wystąpieniami mniejszej liczby 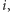 nie zmieniając mocy modyfikowanych zbiorów. Sprawdzając kilka prostych przypadków, można też zauważyć, że operacja
nie zmieniając mocy modyfikowanych zbiorów. Sprawdzając kilka prostych przypadków, można też zauważyć, że operacja 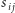 jest różnowartościowa na
jest różnowartościowa na 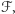 a zatem wynik jej zastosowania do wszystkich zbiorów rodziny, tzn. rodzina
a zatem wynik jej zastosowania do wszystkich zbiorów rodziny, tzn. rodzina 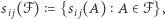 liczy sobie tyle samo elementów co
liczy sobie tyle samo elementów co 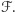 Nazwijmy wagą zbioru
Nazwijmy wagą zbioru 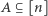 sumę jego elementów, zaś wagą rodziny
sumę jego elementów, zaś wagą rodziny 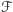 - sumę wag zbiorów należących do
- sumę wag zbiorów należących do 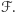 Zauważmy, że waga
Zauważmy, że waga 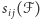 jest nie większa od wagi
jest nie większa od wagi 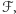 a równość zachodzi wtedy i tylko wtedy, gdy
a równość zachodzi wtedy i tylko wtedy, gdy 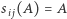 dla każdego
dla każdego 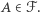 Najciekawsze jednak jest to, że jeśli
Najciekawsze jednak jest to, że jeśli 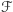 jest rodziną przecinającą się, to jest nią również
jest rodziną przecinającą się, to jest nią również 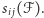 Ponieważ jednak niniejszy artykuł i tak jest bogato udekorowany matematycznymi formułami, techniczny (acz nietrudny) dowód tego faktu pozostawiam Czytelnikowi Dociekliwemu jako ćwiczenie.
Ponieważ jednak niniejszy artykuł i tak jest bogato udekorowany matematycznymi formułami, techniczny (acz nietrudny) dowód tego faktu pozostawiam Czytelnikowi Dociekliwemu jako ćwiczenie.
Potrzebne nam będzie jeszcze jedno pojęcie - rodzinę 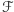 nazwiemy przesuniętą, jeżeli dla każdych
nazwiemy przesuniętą, jeżeli dla każdych 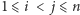 zachodzi
zachodzi 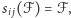 co oznacza tak naprawdę, że
co oznacza tak naprawdę, że 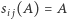 dla każdego
dla każdego 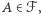 bo rodziny
bo rodziny 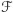 i
i 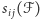 mają taką samą wagę. Równoważnie, rodzina
mają taką samą wagę. Równoważnie, rodzina 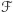 jest przesunięta, jeśli dla każdych liczb
jest przesunięta, jeśli dla każdych liczb 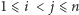 oraz każdego zbioru
oraz każdego zbioru 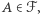 z warunków
z warunków 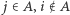 wynika, że
wynika, że 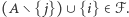 W zbiorach z przesuniętej rodziny
W zbiorach z przesuniętej rodziny 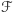 można podmieniać większe liczby na mniejsze, otrzymując dalej zbiory z
można podmieniać większe liczby na mniejsze, otrzymując dalej zbiory z 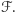
Rozważmy teraz dowolną rodzinę 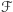 i jeśli istnieją
i jeśli istnieją 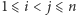 takie, że
takie, że 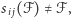 to zastąpmy
to zastąpmy 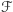 przez
przez 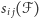 i powtarzajmy tę procedurę, dopóki jest to możliwe. Kiedyś musi się ona zakończyć z uwagi na zmniejszającą się wagę rozważanej rodziny, a zatem z każdej rodziny
i powtarzajmy tę procedurę, dopóki jest to możliwe. Kiedyś musi się ona zakończyć z uwagi na zmniejszającą się wagę rozważanej rodziny, a zatem z każdej rodziny 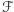 możemy, stosując skończenie wiele operacji postaci
możemy, stosując skończenie wiele operacji postaci 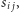 otrzymać rodzinę przesuniętą
otrzymać rodzinę przesuniętą 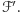
Możemy teraz uzasadnić odpowiedź na pytanie 2. Wykażemy przez indukcję względem 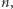 że jeśli
że jeśli 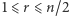 oraz
oraz 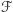 jest
jest 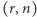 -rodziną, to
-rodziną, to 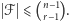
Bazę indukcji stanowi przypadek 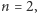 w którym sprawa jest oczywista. Przejdźmy do dowodu kroku indukcyjnego: niech
w którym sprawa jest oczywista. Przejdźmy do dowodu kroku indukcyjnego: niech 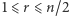 oraz
oraz 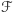 będzie
będzie 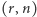 -rodziną. Jeśli
-rodziną. Jeśli 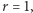 to łatwo zobaczyć, że
to łatwo zobaczyć, że 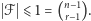 Jeśli zaś
Jeśli zaś 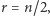 to możemy powtórzyć rozumowanie użyte przy okazji pytania 1 i podzielić
to możemy powtórzyć rozumowanie użyte przy okazji pytania 1 i podzielić  -elementowe podzbiory
-elementowe podzbiory ![[n]](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/9x-a781ff4b22e7ef03aadd7e565ca706fba3a339be-im-33,33,33-FF,FF,FF.gif) na pary postaci
na pary postaci 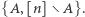 Do każdej z nich należy co najwyżej jeden element rodziny
Do każdej z nich należy co najwyżej jeden element rodziny 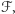 więc
więc 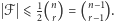
Pozostaje przypadek 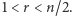 Rodzinę
Rodzinę 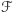 możemy operacjami
możemy operacjami 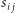 przekształcić do rodziny
przekształcić do rodziny 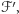 która jest przesunięta, a także, z uwagi na własności zachowywane przez
która jest przesunięta, a także, z uwagi na własności zachowywane przez 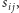 jest
jest 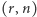 -rodziną i liczy tyle samo elementów, co
-rodziną i liczy tyle samo elementów, co 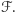 Sprowadziliśmy zatem problem do rodzin przesuniętych. Próbując zredukować problem do podzbiorów
Sprowadziliśmy zatem problem do rodzin przesuniętych. Próbując zredukować problem do podzbiorów ![|[n − 1],](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/8x-c39d8c6e60f6778c53dc34c7323da1e802f09201-im-33,33,33-FF,FF,FF.gif) rozważmy rodziny
rozważmy rodziny 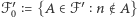 oraz
oraz 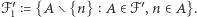
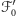 jest z założenia
jest z założenia 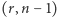 -rodziną oraz
-rodziną oraz 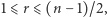 więc na mocy założenia indukcyjnego,
więc na mocy założenia indukcyjnego, 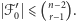
Z kolei 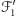 jest
jest 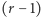 -jednorodną rodziną podzbiorów
-jednorodną rodziną podzbiorów ![[n − 1],](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/3x-8e730a67c9744b2b184047410196ab28d5354426-im-33,33,33-FF,FF,FF.gif) a także
a także 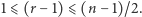 Sprawdźmy, że jest też rodziną przecinającą się, aby móc skorzystać z założenia indukcyjnego. Przypuśćmy nie wprost, że pewne
Sprawdźmy, że jest też rodziną przecinającą się, aby móc skorzystać z założenia indukcyjnego. Przypuśćmy nie wprost, że pewne 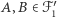 są rozłączne. Ponieważ
są rozłączne. Ponieważ 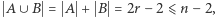 więc istnieje
więc istnieje ![|k∈ [n −1]∖ (A](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/7x-8e730a67c9744b2b184047410196ab28d5354426-im-33,33,33-FF,FF,FF.gif) Do przesuniętej rodziny
Do przesuniętej rodziny 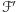 należą zbiory
należą zbiory 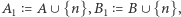 więc należy również do niej
więc należy również do niej 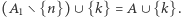 Widać teraz, że
Widać teraz, że 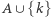 i
i 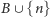 są rozłącznymi elementami przecinającej się rodziny
są rozłącznymi elementami przecinającej się rodziny 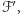 czyli mamy sprzeczność. Z założenia indukcyjnego dostajemy więc
czyli mamy sprzeczność. Z założenia indukcyjnego dostajemy więc 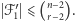
Podsumowując, 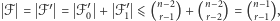 co kończy dowód kroku indukcyjnego i rozwiązanie problemu.
co kończy dowód kroku indukcyjnego i rozwiązanie problemu.
Dość naturalny pomysł na krok indukcyjny mógł zadziałać dopiero po przejściu do rodziny przesuniętej. Otrzymany rezultat znany jest jako twierdzenie Erdősa-Ko-Rado, a przyjrzeliśmy się właśnie jego pierwszemu dowodowi. Na tym się jednak kariera techniki przesuwania w kombinatoryce nie skończyła. Udało się dzięki niej rozwiązać wiele problemów i wciąż jest ona z powodzeniem stosowana.

![|[n]?](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/2x-acdedc4f239bbe472569338869b742bff0f8930e-im-33,33,33-FF,FF,FF.gif)
![[n]](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/1x-d07f1cd96330009e94a7fcaca1b6542e54bb2df9-im-33,33,33-FF,FF,FF.gif) zawierającego
zawierającego 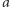 jest równoważny wyborowi pozostałych elementów, czyli dowolnego podzbioru zbioru
jest równoważny wyborowi pozostałych elementów, czyli dowolnego podzbioru zbioru ![|[n] ∖ {a}.](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/3x-d07f1cd96330009e94a7fcaca1b6542e54bb2df9-im-33,33,33-FF,FF,FF.gif)
![[n],](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/1x-5ce5a8ba18193ee766f6dacffb476498fd4fd56b-im-33,33,33-FF,FF,FF.gif) które osiągają
które osiągają 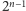 elementów. Te przedstawione nie są jedyne.
elementów. Te przedstawione nie są jedyne.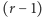 elementów zbioru
elementów zbioru 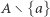 spośród
spośród 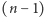 elementów zbioru
elementów zbioru ![[n] ∖ {a}.](/math/temat/matematyka/kombinatoryka/2016/03/22/Kombinatoryka_ekstremalna/4x-d2c264c946d57c906d0f0643f720f8b13f598dfb-im-33,33,33-FF,FF,FF.gif)