Mała Delta

O tym, jak Puchatek podzbiory permutował

Niektórzy znajdują co rano na progu swojego domu butelkę ze świeżym mlekiem. Kubuś Puchatek każdego ranka znajduje tam 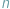$| n$ garnczków miodu. Garnczki są różnej wielkości i Kubuś każdego dnia stara się opróżniać je w innej kolejności...

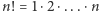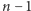Oczywiście, nawet Kubuś wie (po tym, jak mu to wytłumaczył Krzyś), że jest $n! = 1 ⋅2⋅...⋅n$ sposobów, na jakie to może zrobić (na $n$ sposobów może wybrać pierwszy garnczek, na $|n −1$ sposobów drugi itd.). Dziś jednak Kubuś jest w nastroju do niebezpiecznych rozmyślań i zastanawia się, co się stanie, jeśli dopuści możliwość, że może nie opróżnić wszystkich garnczków. "Oczywiście, jest to zupełnie bezsensowne z punktu widzenia misiowego żołądka - pomyślał Kubuś. - Ale ciekawe, jak bardzo zwiększy to liczbę sposobów dokonania wyboru."

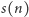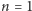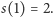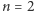Zsumujmy liczbę uporządkowań poszczególnych podzbiorów $n$ -elementowego zbioru garnczków - oznaczmy tę liczbę przez $|s(n)$ i spróbujmy ją obliczyć dla małych przykładów. Dla $n = 1$ mamy dwie możliwości: Kubuś albo opróżni jedyny garnczek, jaki ma, albo nie zrobi tego, zatem $s(1) = 2.$ Dla $|n = 2$ mamy już pięć sposobów postępowania: Kubuś nie robi nic, opróżnia jeden z dwóch garnczków, albo opróżnia oba garnczki w jednej z dwóch kolejności. Natomiast dla trzech garnczków mamy 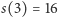$|s(3) = 16$ sposobów (nic, 1, 2, 3, 12, 13, 21, 23, 31, 32, 123, 132, 213, 231, 312, 321). Wyniki dalszych eksperymentów udokumentowane są w tabelce na marginesie.

Z tabelki wynika, że dla małych przykładów 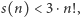$| s(n) < 3 ⋅n!,$ czyli rozważanie uporządkowań podzbiorów zwiększa liczbę sposobów co najwyżej 3 razy. Okazuje się, że tak jest również dla większych $|n.$ Kubuś chętnie podzieliłby się tym odkryciem z Krzysiem, ale do tego potrzebuje je udowodnić. Pomóżmy mu.

Jeśli Kubuś chce danego dnia opróżnić 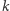$k$ garnczków, to pierwszy garnczek może wybrać na 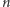$| n$ sposobów, drugi na 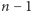$| n− 1$ sposobów, aż do ostatniego, który może wybrać na 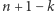$|n+ 1− k$ sposobów. To sumarycznie daje nam 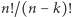$n!/(n − k)!$ możliwości. Sumując po wszystkich możliwych wyborach 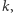$|k,$ dostajemy

n n! n 1 s(n) =Q (n-−-k)! = n! ⋅Q k!. k 0 k 0

Gdybyśmy poprosili o pomoc uczoną Sowę, na pewno podpowiedziałaby nam, że wartość sumy z prawej strony jest rzeczywiście ograniczona przez 3, a dokładniej jest nie większa niż

∞ Q -1 = e ≈ 2,7182818. k 0k!

Z tego wynika, że wartość 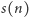$|s(n)$ może być przybliżona przez 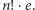$|n!⋅e.$ Pójdźmy krok dalej i obliczmy, jak dobre jest to przybliżenie. Zauważmy, że dla 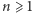$|n⩾ 1$ mamy

$pict$

Skoro zatem 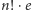$| n!⋅e$ jest większe od całkowitej liczby 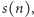$| s(n),$ ale nie więcej niż o 1, to części całkowite tych dwóch liczb muszą być takie same. Dzięki temu w nagrodę za naszą wytrwałość dostajemy zwięzły wzór na poszukiwaną liczbę uporządkowań podzbiorów $|n$ garnczków:

s(n) = ⌊n!⋅e⌋.