Układanie prostokątów
W tym artykule zastanawiamy się nad pytaniem kiedy szachownicę 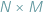 można pokryć prostokątami
można pokryć prostokątami 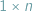 ? Naturalna próba odpowiedzi to: szachownicę można pokryć, gdy
? Naturalna próba odpowiedzi to: szachownicę można pokryć, gdy 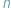 dzieli długość któregoś z boków, czyli gdy
dzieli długość któregoś z boków, czyli gdy 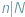 lub
lub 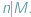 Jasne jest, że w tym przypadku faktycznie można pokryć szachownicę. Ale czy są inne przypadki, w których istnieje pokrycie?
Jasne jest, że w tym przypadku faktycznie można pokryć szachownicę. Ale czy są inne przypadki, w których istnieje pokrycie?
Jeżeli  jest liczbą pierwszą, to łatwo zauważyć, że nie: jeżeli duży prostokąt jest pokryty prostokątami
jest liczbą pierwszą, to łatwo zauważyć, że nie: jeżeli duży prostokąt jest pokryty prostokątami 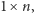 to
to 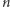 dzieli jego pole, które jest równe
dzieli jego pole, które jest równe 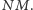 Skoro
Skoro 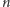 jest pierwsza, to
jest pierwsza, to 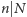 lub
lub 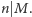
W przypadku, gdy 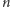 nie jest pierwsza, sprawa nie jest taka prosta. Istnieje sporo klasycznych zadań z tej problematyki, dotyczących szczególnych przypadków tego pytania (patrz np. deltoid 4/2010). Okazuje się, że łatwiej dojść do rozwiązania, gdy potraktuje się problem ogólnie. Kluczem jest, jak we wspomnianym deltoidze, metoda kolorowania.
nie jest pierwsza, sprawa nie jest taka prosta. Istnieje sporo klasycznych zadań z tej problematyki, dotyczących szczególnych przypadków tego pytania (patrz np. deltoid 4/2010). Okazuje się, że łatwiej dojść do rozwiązania, gdy potraktuje się problem ogólnie. Kluczem jest, jak we wspomnianym deltoidze, metoda kolorowania.

Rys. 1

Rys. 2
Pokolorujmy kolejne przekątne szachownicy 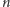 kolorami (na rysunku 1 mamy
kolorami (na rysunku 1 mamy 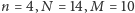 ). Do dalszych rozważań potrzeba nam nieco oznaczeń i obserwacji. W większości przypadków znacznie łatwiej przekonać się o prawdziwości podanych stwierdzeń, np. patrząc na rysunek, niż porządnie opisać dowód, zatem uzupełnienie uzasadnień pozostawiamy Czytelnikowi.
). Do dalszych rozważań potrzeba nam nieco oznaczeń i obserwacji. W większości przypadków znacznie łatwiej przekonać się o prawdziwości podanych stwierdzeń, np. patrząc na rysunek, niż porządnie opisać dowód, zatem uzupełnienie uzasadnień pozostawiamy Czytelnikowi.
- 1. Pola o tym samym kolorze leżące w tym samym rzędzie lub kolumnie są oddalone o dokładnie
 Wynika stąd kluczowy wniosek: każdy prostokąt
Wynika stąd kluczowy wniosek: każdy prostokąt 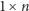 zakrywa dokładnie jedno pole każdego koloru.
zakrywa dokładnie jedno pole każdego koloru. - 2. Mówimy, że rząd ma kolor
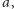 jeżeli zaczyna się od pola koloru
jeżeli zaczyna się od pola koloru 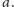
- 3. Jeżeli
 nie dzieli
nie dzieli 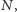 to rzędów niektórych kolorów jest o jeden więcej, niż rzędów pozostałych kolorów. Te kolory nazywamy częstymi. Pozostałe kolory nazywamy nieczęstymi. Na rysunku 1 czerwony i jasnoszary są częste, a pozostałe nieczęste. Jeżeli
to rzędów niektórych kolorów jest o jeden więcej, niż rzędów pozostałych kolorów. Te kolory nazywamy częstymi. Pozostałe kolory nazywamy nieczęstymi. Na rysunku 1 czerwony i jasnoszary są częste, a pozostałe nieczęste. Jeżeli 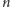 dzieli
dzieli 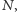 to wszystkie kolory nazywamy częstymi.
to wszystkie kolory nazywamy częstymi. - 4. Jeżeli jest dokładnie
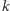 kolorów częstych, to
kolorów częstych, to 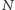 daje resztę
daje resztę 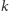 z dzielenia przez
z dzielenia przez 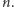
- 5. Kolorowanie pozwala rozróżniać rzędy. Jeżeli
 nie dzieli
nie dzieli 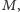 a rząd
a rząd 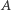 i rząd
i rząd 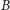 mają różne kolory, to istnieje taki kolor
mają różne kolory, to istnieje taki kolor 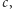 że liczba pól pokolorowanych na
że liczba pól pokolorowanych na  jest różna w
jest różna w 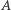 i
i 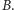
- 6. Przemalowywanie. Wybierzmy dwa kolory
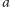 i
i 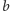 i przemalujmy każdy rząd koloru
i przemalujmy każdy rząd koloru 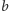 na rząd koloru
na rząd koloru 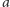 i odwrotnie. Na rysunku 2 rzędy czerwone przemalowano na ciemnoszare i odwrotnie. Następująca obserwacja jest kluczowa:
i odwrotnie. Na rysunku 2 rzędy czerwone przemalowano na ciemnoszare i odwrotnie. Następująca obserwacja jest kluczowa:
po przemalowaniu każdy prostokąt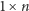 zakrywa dokładnie jedno pole każdego koloru.
zakrywa dokładnie jedno pole każdego koloru.
Oczywiście, wszystkie powyższe obserwacje przenoszą się na kolumny - wystarczy zamienić 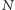 z
z 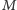 w sformułowaniach powyżej.
w sformułowaniach powyżej.
Możemy już przejść do rozwiązania naszego problemu.
Dowód. Wiemy, że jeśli 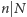 lub
lub 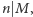 to pokrycie istnieje. Wykażemy, że zachodzi również implikacja odwrotna: jeżeli istnieje pokrycie, to
to pokrycie istnieje. Wykażemy, że zachodzi również implikacja odwrotna: jeżeli istnieje pokrycie, to 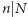 lub
lub 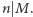
Załóżmy, że szachownicę 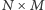 można pokryć prostokątami
można pokryć prostokątami 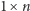 oraz liczba
oraz liczba 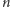 nie dzieli ani
nie dzieli ani 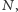 ani
ani 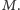 Pokolorujmy szachownicę
Pokolorujmy szachownicę  kolorami, podobnie jak na rysunku 1. Z obserwacji 1 wynika, że pól każdego koloru jest tyle samo.
kolorami, podobnie jak na rysunku 1. Z obserwacji 1 wynika, że pól każdego koloru jest tyle samo.
Skoro  nie dzieli
nie dzieli 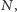 to istnieje przynajmniej jeden kolor nieczęsty. Wybierzmy dowolny kolor częsty
to istnieje przynajmniej jeden kolor nieczęsty. Wybierzmy dowolny kolor częsty 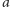 i dowolny kolor nieczęsty
i dowolny kolor nieczęsty 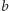 i przemalujmy rzędy
i przemalujmy rzędy 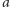 na
na 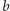 i odwrotnie (jak w przykładzie na rysunku 2).
i odwrotnie (jak w przykładzie na rysunku 2).
Na mocy obserwacji 6 po przemalowaniu każdy prostokąt zawiera  pól o różnych kolorach, więc pól każdego koloru jest nadal tyle samo. Z drugiej strony, ubył jeden rząd
pól o różnych kolorach, więc pól każdego koloru jest nadal tyle samo. Z drugiej strony, ubył jeden rząd 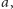 przybył zaś jeden rząd
przybył zaś jeden rząd 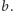 Z obserwacji 5 wynika, że liczba pól pokolorowanych na pewien kolor
Z obserwacji 5 wynika, że liczba pól pokolorowanych na pewien kolor  zmieniła się, zatem mamy sprzeczność.
zmieniła się, zatem mamy sprzeczność.
Można zastanawiać się też, kiedy istnieje pokrycie szachownicy z wyciętymi polami: rogami, polem środkowym itp. Przyjrzyjmy się najprostszej modyfikacji zadania, czyli szachownicy z wyciętym jednym polem.
Zadanie 2. Uzasadnij, że szachownicę 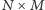 z wyciętym polem o współrzędnych
z wyciętym polem o współrzędnych 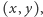 jak na rysunku 3, można pokryć prostokątami
jak na rysunku 3, można pokryć prostokątami 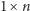 wtedy i tylko wtedy, gdy zachodzi jeden z warunków:
wtedy i tylko wtedy, gdy zachodzi jeden z warunków:
- 1.
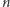 dzieli każdą z liczb
dzieli każdą z liczb 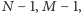
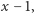
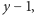
- 2.
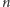 dzieli każdą z liczb
dzieli każdą z liczb 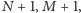
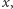
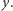
Dowód. Jak zwykle Czytelnikowi pozostawiamy udowodnienie, że gdy któryś z warunków zachodzi, to pokrycie istnieje; prostokąty można wtedy ułożyć w cztery duże "bloki", patrz rysunek 4 dla pokrycia z 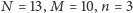 oraz
oraz 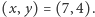
Załóżmy zatem, że pokrycie prostokąta istnieje. Na początek chcemy rozważyć rzędy i stwierdzić, że
liczba
dzieli liczby
i
lub liczba
dzieli liczby
i
.
Niech 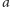 będzie kolorem rzędu zawierającego wycięte pole. Załóżmy, że
będzie kolorem rzędu zawierającego wycięte pole. Załóżmy, że  jest częsty. Jeżeli istnieje inny kolor częsty
jest częsty. Jeżeli istnieje inny kolor częsty 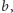 to przemalowujemy
to przemalowujemy 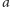 na
na 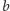 i
i 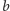 na
na 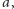 jak w obserwacji 6. Pomijając wycięte pole, przemalowanie to nie zmienia liczby pól danego koloru na szachownicy, gdyż szachownica zawiera tyle samo rzędów koloru
jak w obserwacji 6. Pomijając wycięte pole, przemalowanie to nie zmienia liczby pól danego koloru na szachownicy, gdyż szachownica zawiera tyle samo rzędów koloru 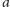 i
i 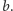 Skoro rzędy
Skoro rzędy 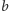 i
i  są różnych kolorów, to pole w kolumnie
są różnych kolorów, to pole w kolumnie 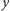 miało w tych rzędach różny kolor. Wobec tego po przemalowaniu liczba pól pewnego koloru zmniejszy się o jeden.
miało w tych rzędach różny kolor. Wobec tego po przemalowaniu liczba pól pewnego koloru zmniejszy się o jeden.
Z drugiej strony, prostokąt pokryty był prostokątami 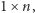 więc pól każdego koloru przed i po przemalowaniu jest tyle samo:
więc pól każdego koloru przed i po przemalowaniu jest tyle samo: 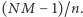 Zatem przemalowanie nie może zmieniać liczby pól żadnego koloru.
Zatem przemalowanie nie może zmieniać liczby pól żadnego koloru.
Sprzeczność pokazuje, że tylko kolor 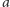 jest częsty. Z obserwacji 4 wynika, że
jest częsty. Z obserwacji 4 wynika, że 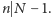 Zauważmy ponadto, że
Zauważmy ponadto, że 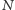 -ty rząd ma kolor częsty, a więc kolor
-ty rząd ma kolor częsty, a więc kolor 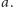 Wobec tego
Wobec tego 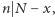 czyli
czyli 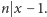
Podobnie rozumujemy, gdy 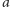 jest nieczęstym kolorem: stwierdzamy, że jest on jedynym nieczęstym kolorem, więc częstych kolorów jest
jest nieczęstym kolorem: stwierdzamy, że jest on jedynym nieczęstym kolorem, więc częstych kolorów jest 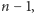 stąd
stąd 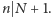 Ponadto rząd
Ponadto rząd  -ty ma kolor nieczęsty, więc
-ty ma kolor nieczęsty, więc 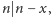 czyli
czyli 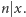
Popatrzmy teraz na kolumny. Podobnie jak w przypadku rzędów stwierdzamy, że
liczba
dzieli
i
lub liczba
dzieli
i
.
Mamy łącznie cztery możliwości: dwie na mocy rozumowania "o rzędach" i dwie "o kolumnach". Chcemy teraz wyeliminować możliwości 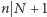 i
i 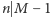 oraz
oraz 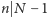 i
i 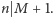 Załóżmy najpierw, że
Załóżmy najpierw, że 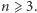 Skoro prostokąty o polu
Skoro prostokąty o polu 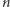 pokrywają szachownicę z wyciętym polem, która ma pole powierzchni
pokrywają szachownicę z wyciętym polem, która ma pole powierzchni 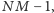 to
to 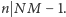 Gdyby
Gdyby 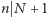 i
i 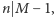 to
to 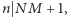 więc
więc 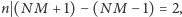 co daje sprzeczność. Podobnie przypadek
co daje sprzeczność. Podobnie przypadek 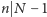 i
i 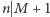 prowadzi do sprzeczności. To kończy rozumowanie w przypadku
prowadzi do sprzeczności. To kończy rozumowanie w przypadku 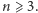

Rys. 3

Rys. 4
Na koniec rozważmy przypadek 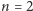 i załóżmy, że
i załóżmy, że  dzieli liczby
dzieli liczby 
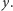 Wobec tego liczby
Wobec tego liczby 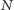 i
i 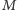 są nieparzyste. Nazwijmy kolor pola narożnego białym, zaś drugi kolor czarnym. Na pełnej szachownicy o nieparzystych długościach boków pól białych jest więcej niż czarnych. Zatem, jeżeli istnieje pokrycie szachownicy z wyciętym polem
są nieparzyste. Nazwijmy kolor pola narożnego białym, zaś drugi kolor czarnym. Na pełnej szachownicy o nieparzystych długościach boków pól białych jest więcej niż czarnych. Zatem, jeżeli istnieje pokrycie szachownicy z wyciętym polem 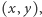 to pole to ma kolor biały. To znaczy, że
to pole to ma kolor biały. To znaczy, że 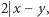 i otrzymujemy sprzeczność z podzielnościami
i otrzymujemy sprzeczność z podzielnościami 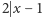 oraz
oraz 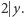 To samo rozumowanie eliminuje przypadek, gdy
To samo rozumowanie eliminuje przypadek, gdy 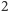 dzieli liczby
dzieli liczby 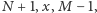

Jak widać, przedstawiona metoda jest ogólna, w tym znaczeniu, że przy odrobinie czasu i cierpliwości można ją zastosować, na przykład, do szachownicy z rozsądną liczbą wyciętych pól. Na zachętę pozostawiamy Czytelnikowi kilka problemów.
Zadanie 3. Uzasadnić, że jeżeli 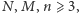 to szachownicę
to szachownicę 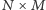 z usuniętymi dwoma przeciwległymi rogami można pokryć prostokątami
z usuniętymi dwoma przeciwległymi rogami można pokryć prostokątami 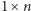 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 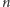 dzieli każdą z liczb
dzieli każdą z liczb 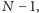
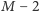 lub
lub 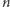 dzieli każdą z liczb
dzieli każdą z liczb 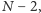
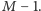 Wskazówka
Wskazówka
Zadanie 4. Dla których całkowitych 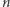 szachownicę
szachownicę 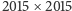 z wyciętym środkowym polem można pokryć prostokątami
z wyciętym środkowym polem można pokryć prostokątami 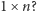 Wskazówka
Wskazówka
Zadanie 5. Dla których całkowitych  szachownicę
szachownicę 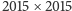 z wyciętym narożnym polem można pokryć prostokątami
z wyciętym narożnym polem można pokryć prostokątami 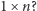 Wskazówka
Wskazówka
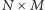
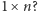
 kolorów jak w poprzednich przykładach. Załóżmy, że pierwszy rząd jest koloru
kolorów jak w poprzednich przykładach. Załóżmy, że pierwszy rząd jest koloru 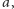 zaś drugi - koloru
zaś drugi - koloru 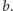 Jeżeli
Jeżeli 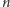 nie dzieli ani
nie dzieli ani 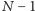 ani
ani  to rzędów kolorów
to rzędów kolorów 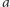 i
i 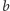 jest tyle samo, zaś ostatni rząd nie jest koloru
jest tyle samo, zaś ostatni rząd nie jest koloru 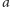 ani
ani 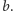 Przemalowujemy rzędy koloru
Przemalowujemy rzędy koloru 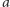 na kolor
na kolor 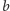 i odwrotnie i sprawdzamy, że po tej zamianie liczba pól pewnego koloru zmieniła się. To daje sprzeczność. Podobnie uzasadniamy, że
i odwrotnie i sprawdzamy, że po tej zamianie liczba pól pewnego koloru zmieniła się. To daje sprzeczność. Podobnie uzasadniamy, że 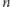 dzieli
dzieli 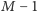 lub
lub 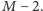
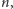 które spełniają jeden z warunków
które spełniają jeden z warunków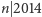 oraz
oraz 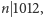
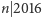 oraz
oraz 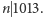
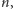 które są dzielnikami
które są dzielnikami 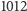 lub
lub 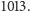
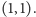 Na podstawie zadania 2 szukamy liczb
Na podstawie zadania 2 szukamy liczb  które spełniają jeden z warunków
które spełniają jeden z warunków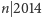 oraz
oraz 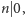
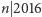 oraz
oraz 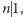 czyli
czyli 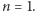
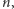 które są dzielnikami
które są dzielnikami 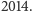
 kolejnych pól (w rzędzie lub kolumnie).
kolejnych pól (w rzędzie lub kolumnie).