Kombinatoryka i nieskończoność
Kombinatoryka zajmuje się własnościami zbiorów skończonych, w szczególności zagadnieniem zliczania elementów takich zbiorów. Czy może zatem w kombinatoryce znaleźć się miejsce dla nieskończoności? Okazuje się, że tak – pokażę jedno z takich zastosowań nieskończoności: funkcje tworzące...
Zacznę od następującego zadania:

Rys. 1
Oznaczmy przez
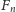 liczbę dróg żaby na
liczbę dróg żaby na
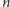 -ty kamień.
Oczywiście,
-ty kamień.
Oczywiście,
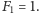 Na kamień z numerem 1 żaba może bowiem
dostać się tylko w jeden sposób – ma wykonać jeden pojedynczy skok
(Rys. 1).
Na kamień z numerem 1 żaba może bowiem
dostać się tylko w jeden sposób – ma wykonać jeden pojedynczy skok
(Rys. 1).

Rys. 2
Następnie
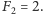 Na kamień z numerem 2 żaba może dostać się
dwoma sposobami – wykonać dwa skoki pojedyncze lub jeden podwójny
(Rys. 2).
Na kamień z numerem 2 żaba może dostać się
dwoma sposobami – wykonać dwa skoki pojedyncze lub jeden podwójny
(Rys. 2).
Zobaczmy teraz, na ile sposobów żaba może się dostać na kamień o numerze
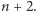 Ma ona
Ma ona
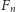 różnych dróg na kamień o numerze
różnych dróg na kamień o numerze
 i
i
 dróg na kamień o numerze
dróg na kamień o numerze
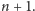 Ponieważ
ostatni skok żaby jest skokiem podwójnym z kamienia o numerze
Ponieważ
ostatni skok żaby jest skokiem podwójnym z kamienia o numerze
 lub pojedynczym z kamienia o numerze
lub pojedynczym z kamienia o numerze
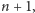 więc łącznie
istnieje
więc łącznie
istnieje
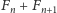 dróg żaby na kamień
dróg żaby na kamień
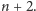 A więc
A więc
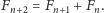 Zatem na trzeci kamień żaba może dostać się na
Zatem na trzeci kamień żaba może dostać się na
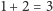 sposoby, na czwarty na
sposoby, na czwarty na
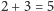 sposobów i tak dalej.
Zauważmy, że jeśli przyjmiemy
sposobów i tak dalej.
Zauważmy, że jeśli przyjmiemy
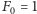 (co jest całkiem naturalne:
istnieje jeden sposób dostania się na kamień o numerze 0, mianowicie nie
robić nic), to okaże się, że
(co jest całkiem naturalne:
istnieje jeden sposób dostania się na kamień o numerze 0, mianowicie nie
robić nic), to okaże się, że
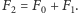 Zatem ciąg
Zatem ciąg
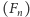 jest
określony wzorami
jest
określony wzorami

Ten ciąg jest dobrze znany w matematyce: jest to tzw. ciąg Fibonacciego.
Powyższy wzór definiujący ten ciąg jest wzorem rekurencyjnym: kolejny
wyraz ciągu nie jest zdefiniowany wzorem uzależniającym ten wyraz
od indeksu
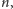 ale w zależności od wyrazów poprzednich.
Powstaje pytanie, czy możemy znaleźć wzór ogólny, zależny tylko od
ale w zależności od wyrazów poprzednich.
Powstaje pytanie, czy możemy znaleźć wzór ogólny, zależny tylko od
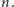 Jedna z metod otrzymywania wzorów ogólnych korzysta z tzw.
funkcji tworzących.
Jedna z metod otrzymywania wzorów ogólnych korzysta z tzw.
funkcji tworzących.
Definiujemy funkcję tworzącą dla ciągu Fibonacciego wzorem

Mamy teraz

Otrzymaliśmy równanie

z którego dostajemy wzór na
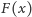 :
:

Teraz otrzymaną funkcję tworzącą rozwijamy w szereg potęgowy. W tym celu rozkładamy ułamek

na tzw. ułamki proste. Szczegóły obliczeń pominę tutaj; Czytelnik może się natomiast łatwo przekonać (dodając ułamki), że

gdzie

Korzystamy teraz ze znanego wzoru na sumę nieskończonego szeregu
geometrycznego. Mianowicie dla dowolnej liczby
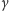 i takiej liczby
i takiej liczby
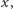 że
że
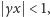 mamy
mamy

Stąd dostajemy rozwinięcie funkcji
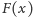 w szereg potęgowy
w szereg potęgowy

Porównując współczynniki przy kolejnych potęgach
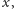 dostajemy
następujący wzór ogólny:
dostajemy
następujący wzór ogólny:

Ten wzór jest nazywany wzorem Bineta.

Zauważmy, że w tej metodzie otrzymywania wzoru ogólnego konieczne było
rozwijanie funkcji w nieskończony szereg potęgowy. Tak więc nieskończoność
została użyta nie tylko w znaczeniu potencjalnym (wzór obowiązuje dla
każdej, dowolnie dużej, ale skończonej liczby
 ), ale w znaczeniu
aktualnym: mamy do czynienia z rzeczywiście nieskończonym szeregiem
potęgowym.
), ale w znaczeniu
aktualnym: mamy do czynienia z rzeczywiście nieskończonym szeregiem
potęgowym.