Deltoid
Suma trzecich potęg
Rozważmy szachownicę
 Policzmy dwoma niezależnymi
sposobami, ile jest na niej prostokątów o bokach wzdłuż linii podziału na
kratki.
Policzmy dwoma niezależnymi
sposobami, ile jest na niej prostokątów o bokach wzdłuż linii podziału na
kratki.
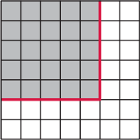
Rys. 1 Szary obszar to piąte naroże, kolorem zaznaczono jego brzeg.

Rys. 2 Dla piątego naroża liczymy kolorowe prostokąty, natomiast nie liczymy czarnych, bo mieściły się one w mniejszych narożach.

Rys. 3
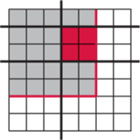
Rys. 4
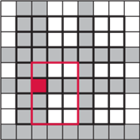
Rys. 5 Szarym wypełnieniem oznaczono wybrane wiersze i kolumny, kolorem – prostokąt i jego wyróżnioną kratkę.
Sposób 1. Dla
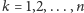 nazwijmy
nazwijmy
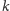 -tym narożem
szachownicy jej lewą górną część o rozmiarach
-tym narożem
szachownicy jej lewą górną część o rozmiarach
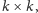 a brzegiem
tego naroża nazwijmy dwa jego boki: prawy i dolny (Rys. 1). Prostokąty
zliczajmy wedle tego, w którym narożu się mieszczą. Prostokąt, który
mieści się w
a brzegiem
tego naroża nazwijmy dwa jego boki: prawy i dolny (Rys. 1). Prostokąty
zliczajmy wedle tego, w którym narożu się mieszczą. Prostokąt, który
mieści się w
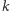 -tym narożu, mieści się też we wszystkich większych
narożach. Aby nie liczyć takich prostokątów wielokrotnie, dla każdego
naroża liczmy tylko te, które dotykają jego brzegu (Rys. 2). Wtedy każdy
prostokąt policzymy dokładnie raz – tylko przy najmniejszym narożu,
w którym się mieści.
-tym narożu, mieści się też we wszystkich większych
narożach. Aby nie liczyć takich prostokątów wielokrotnie, dla każdego
naroża liczmy tylko te, które dotykają jego brzegu (Rys. 2). Wtedy każdy
prostokąt policzymy dokładnie raz – tylko przy najmniejszym narożu,
w którym się mieści.
Ile prostokątów mieści się w
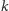 -tym narożu i dotyka jego
brzegu? Taki prostokąt może dotykać obydwu boków z brzegu albo tylko
jednego z nich. Prostokąt pierwszego z tych rodzajów (Rys. 3) można
utożsamić z poziomą prostą wyznaczającą jego górny bok i pionową
wyznaczającą bok lewy. Tego typu prostokątów jest więc
-tym narożu i dotyka jego
brzegu? Taki prostokąt może dotykać obydwu boków z brzegu albo tylko
jednego z nich. Prostokąt pierwszego z tych rodzajów (Rys. 3) można
utożsamić z poziomą prostą wyznaczającą jego górny bok i pionową
wyznaczającą bok lewy. Tego typu prostokątów jest więc
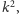 bo prostą
w każdym z kierunków można wybrać na
bo prostą
w każdym z kierunków można wybrać na
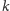 sposobów.
sposobów.
Każdy prostokąt dotykający tylko prawego boku naroża (Rys. 4)
można utożsamić z prostą pionową wyznaczającą lewy bok prostokąta
(jest
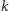 możliwych takich prostych) oraz z parą różnych prostych
poziomych wyznaczających jego poziome boki (par jest
możliwych takich prostych) oraz z parą różnych prostych
poziomych wyznaczających jego poziome boki (par jest
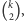 bo
wybieramy dwie proste spośród
bo
wybieramy dwie proste spośród
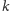 ). Takich prostokątów jest więc
). Takich prostokątów jest więc
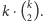 Prostokątów dotykających tylko dolnego boku naroża jest
tyle samo.
Prostokątów dotykających tylko dolnego boku naroża jest
tyle samo.
Wszystkich prostokątów w
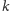 -tym narożu, dotykających jego
brzegu, jest więc
-tym narożu, dotykających jego
brzegu, jest więc

Wobec tego wszystkich prostokątów na szachownicy jest
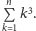
Sposób 2. Każdy prostokąt można
utożsamić z dwiema parami prostych zawierających jego boki. Oznacza to,
że prostokątów jest tyle, na ile sposobów można na szachownicy wybrać
parę różnych prostych pionowych i parę różnych prostych poziomych.
Prostych w każdym z kierunków jest
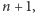 wybrać dwie można
na
wybrać dwie można
na
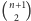 sposobów, zatem prostokątów jest
sposobów, zatem prostokątów jest
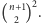
Wniosek. Z powyższych dwóch rozwiązań wynika równość

W połączeniu ze znanym wzorem
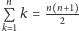 uzyskujemy
uzyskujemy
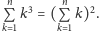
***
Jaka jest suma pól wszystkich rozważanych prostokątów?
Rozwiązanie. Każdy prostokąt „wnosi” do sumy pól tyle, z ilu
jednostkowych kratek szachownicy się składa. Suma pól równa jest więc
liczbie par
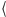 prostokąt, należąca do niego kratka
prostokąt, należąca do niego kratka
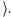 Ile jest
takich par?
Ile jest
takich par?
Dobudujmy do naszej szachownicy
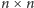 po jednej pomocniczej
kolumnie z lewej i z prawej oraz po jednym wierszu, na górze i na dole.
Otrzymujemy
szachownicę
po jednej pomocniczej
kolumnie z lewej i z prawej oraz po jednym wierszu, na górze i na dole.
Otrzymujemy
szachownicę
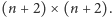 Wybierzmy trzy różne kolumny
(można to zrobić na
Wybierzmy trzy różne kolumny
(można to zrobić na
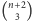 sposoby) oraz trzy różne wiersze (na
tyle samo sposobów). Taki wybór można utożsamić z wybraniem
prostokąta i jego kratki: prostokąt to obszar pomiędzy pierwszą a trzecią
z wybranych kolumn oraz pomiędzy pierwszym a trzecim z wybranych
wierszy, zaś jego wyróżniona kratka jest na skrzyżowaniu środkowej
z wybranych kolumn ze środkowym z wybranych wierszy (Rys. 5).
sposoby) oraz trzy różne wiersze (na
tyle samo sposobów). Taki wybór można utożsamić z wybraniem
prostokąta i jego kratki: prostokąt to obszar pomiędzy pierwszą a trzecią
z wybranych kolumn oraz pomiędzy pierwszym a trzecim z wybranych
wierszy, zaś jego wyróżniona kratka jest na skrzyżowaniu środkowej
z wybranych kolumn ze środkowym z wybranych wierszy (Rys. 5).
Wobec tego par
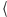 prostokąt, należąca do
niego kratka
prostokąt, należąca do
niego kratka
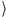 jest
jest
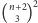 i taka jest też szukana suma pól
wszystkich prostokątów na szachownicy.
i taka jest też szukana suma pól
wszystkich prostokątów na szachownicy.